Нейросетевые преобразователи импульсно-аналоговых сигналов: Учебное пособие, страница 14

В результате обучения исходной сети, описываемой системой (2.19), также получено решение, позволяющее при формировании (2.17) сократить в два раза число  нейронов ее скрытого слоя за счет увеличения нулевых связей между ним и выходным слоем. В итоге найдены значения порогов  () и  () нейронов 1‑го и 2‑го слоев ИНС-преобразователя, а также веса синаптических связей сети, отраженные матрицами  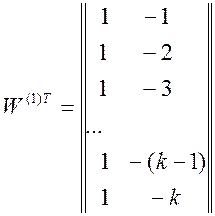и :

 и 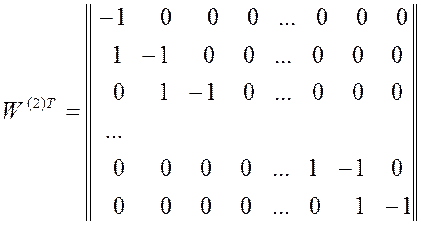 .              (2.25)

2.3.2.Трехслойная персептронная модель структуры ПФИ

 с двоично-взвешенным позиционным кодированием

Применение трехслойных нейронных сетей нашло особенно широкое применение в задачах аппроксимации нелинейных функций, при решении которых использование двухслойных сетей не обеспечивает требуемую погрешность приближения.

Ниже рассматриваются этапы построения нейросетевой модели структуры аналого-цифрового преобразователя  с двоично-позиционным способом кодирования цифрового эквивалента  (1.18).

Выбор архитектуры сети. В основу построения модели преобразователя  положен трехслойный персептрон. Как видно из формулы (1.18) и рис. 2.2,в, для нахождения значений  требуется построить несколько непересекающихся плоскостей (конкретное число плоскостей зависит от номера разряда  и числа разрядов  эквивалента ), каждая из которых задается двумя пороговыми прямыми, что говорит о необходимости применения для формирования результата (1.18) трехслойного персептрона, имеющего матричное описание в виде:

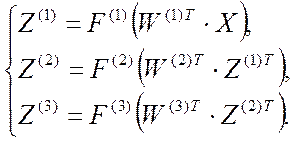                                       (2.26)

Аналитическое описание исходной 3‑слойной аппроксимирующей сети, полученное на основе (2.26), представляется как:

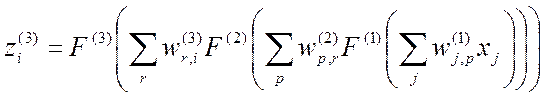,  ,          (2.27)

где  и  – ее входные и выходные сигналы;  – число ее выходов;

,  и  – пороговые функции активации вида (2.3).

Выбор исходной структуры ИНС. При формировании матрицы  выходных сигналов данной нейросети следует учитывать фиксированное местоположение бит позиционного кода  (1.18). Поэтому для  матрица , представленная в виде матрицы-столбца этих сигналов, будет отражать результат как упорядоченную последовательность бит  в виде  или .

При преобразовании  в качестве входных сигналов  и  сети соответственно выступают преобразуемая величина  и эталон преобразования , определяющие число  нейронов входного слоя, равное , и вид матрицы :

.

Как и в рассмотренных выше моделях, операцию аналого-цифрового преобразования осуществляют нейроны  первого скрытого слоя.

В качестве выходных сигналов рассматриваемой сети выступают значения бит  (), формируемые нейронами  выходного слоя. Поэтому число нейронов  выходного слоя равно . Необходимое число  и  нейронов скрытых слоев определится на этапе обучения. Операцию аналого-цифрового преобразования осуществляют нейроны  первого слоя. Из этого следует, что выходные сигналы нейроузлов скрытых и выходного слоев представляются в виде значений бит унитарного эквивалента, поэтому для их получения используются функции активации вида (2.3).

С учетом количества  и  нейронов, составляющих входной и выходной слои соответственно, трехслойная персептронная сеть (2.27), реализующая операцию преобразования , описывается зависимостью:

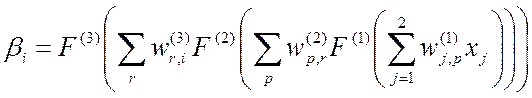,    ,               (2.28)

где ; ; ,  и  – функции активации вида (2.3).

Зависимость (2.28) в матричной форме для всех бит эквивалента  примет вид:

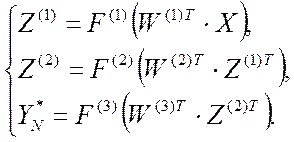                                       (2.29)

где  – матрица-строка, состоящая из входных аналоговых величин;

,  и  – транспонированные матрицы весовых коэффициентов между распределительным и первым, первым и вторым, а также между вторым и выходным слоями;

 и  – матрицы-столбцы, состоящие из выходных сигналов скрытых слоев;

 – матрица-столбец, состоящая из бит позиционного эквивалента , образующих результат преобразования.

Предлагаемая нейросетевая модель преобразователя, реализующая аналитическую зависимость (2.28) и матричную (2.29), показана на рис. 2.6.

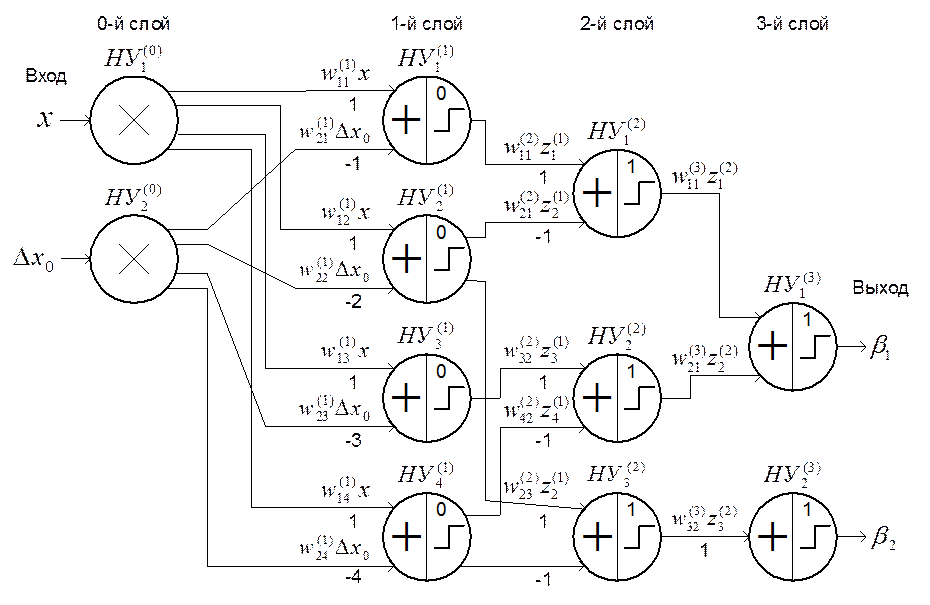
Рис. 2.6. Нейросетевая структура преобразователя  с формированием  на основе трехслойного персептрона (для числа разрядов )

Для 3-слойной структуры время преобразования , затрачиваемое на формирование цифрового эквивалента , находится следующим образом:

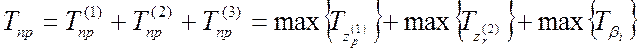,                   (2.30)

где  – время преобразования аналоговой переменной  в бит ;

 и  – времена вычисления бита  на основе значений  () и бита  на основе значений  () соответственно.

Поскольку на 2‑м и 3‑м слоях сеть оперирует логическими (двоичными) переменными, то последними двумя слагаемыми в зависимости (2.30) можно пренебречь. Поэтому

.

Обучение ИНС. Обучение персептрона со скрытыми слоями целесообразно осуществлять с использованием алгоритма обратного распространения ошибки. С целью настройки синаптических связей он использует метод градиентного спуска в пространстве весовых коэффициентов и порогов нейронной сети. Полученные в результате обучения значения весовых коэффициентов  для двухразрядного эквивалента  показаны на рис. 2.6 и определены в виде матриц:

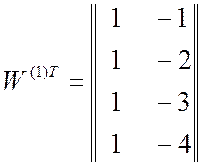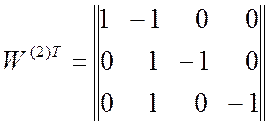,   и 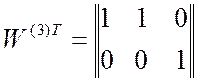.          (2.31)

Величины порогов для активационных функций  в результате обучения имеют вид:

,  и ,

где , , .

Следует отметить, что матрицы весовых коэффициентов (2.31) не являются единственным решением поставленной задачи. Так, например, элементы  и  матрицы  могут принять значения "2" и "‑2" соответственно, что также будет решением задачи преобразования  (1.18). Однако аппаратные затраты на реализацию связей , формируемых в результате умножения аналоговой переменной  на цифровой вес  с формированием результата в виде аналоговой величины, зависят от значения веса . Так, если , то аппаратные затраты на реализацию связи  равны нулю. В связи с этим среди множества решений целесообразно выбирать такую матрицу , в которой содержится наибольшее число элементов  с нулевыми и единичными значениями.

На этапе обучения сети также определено количество  и  нейронов ее скрытых слоев, необходимое для решения поставленной задачи преобразования в зависимости от числа  разрядов эквивалента :

,      .