Нейросетевые преобразователи импульсно-аналоговых сигналов: Учебное пособие, страница 5

1.3.1. Интерпретация линейного преобразования  в виде кусочно-ступенчатой аппроксимации, подходы к ее реализации на основе операций математического нейрона

Процесс линейного преобразования аналоговой величины  в ее цифровой эквивалент  при таком подходе можно представить в виде кусочно-ступенчатой аппроксимации (КСА) линейно-непрерывной (идеализированной) зависимости , где  – масштаб преобразования, приближающей функцией (рис. 1.6):

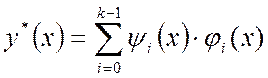,                                          (1.6)

где  – функции логики включения базовых функций , принимающие значения 0 или 1 в зависимости от принадлежности аргумента  ‑му участку аппроксимации  размером , ;

 – число интервалов аппроксимации на диапазоне , причем  для двоично-взвешенного кодирования  с помощью  разрядов.

Принимается (рис. 1.6), что начальное значение , если .

Выбор вида функции , формирующей ‑й участок КСА, и логики формирования  во многом зависит от способа представления значений результата  в виде унитарного  или двоично-позиционного кода .

Так, для унитарного число-импульсного способа кодирования, при котором минимальному значению  соответствует код , следующему – , а максимальному – , функции  целесообразно представлять в виде единичных приращений ординат , а формируемые значения бит  кода  отображать посредством . С учетом этого кусочно-ступенчатая аппроксимирующая зависимость (1.6), описывающая процесс преобразования  для указанного способа представления , будет иметь вид:

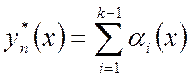,                                           (1.7)

где  – функции включения в  конечных разностей .

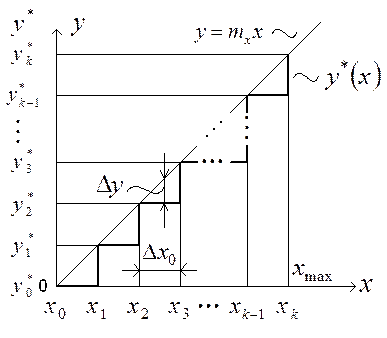
Рис. 1.6. Интерпретация линейного преобразования  в виде КСА зависимостью (1.6)

В связи с аппроксимацией функции  (см. рис. 1.6) зависимостью (1.6) методическая погрешность ее приближения 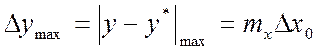 как ошибка преобразования  зависит от числа участков аппроксимации , определяющего, в свою очередь, значение дискрета (интервала)  на диапазоне .

Для обеспечения приведенной погрешности  линейного преобразования , не превышающей заданного (допустимого) значения , необходимо выбрать такой интервал аппроксимации  и соответственно число , чтобы , а , где  – операция определения ближайшего большего целого. При преобразовании  с ошибкой  количество разрядов  для представления  выбирается из соотношения: .

Необходимо отметить, что точность и быстродействие импульсно-цифровых преобразователей  являются взаимосвязанными характеристиками. В них чем меньше погрешность преобразования , тем больше время преобразования , затрачиваемое на получение нового значения цифрового эквивалента аналоговой переменной. Так, для преобразователей временного интервала и частоты в код ( и ) величина  соответственно определяется из соотношений:

 и .

Это объясняется тем, что, например, квантование временных отрезков , определяющих величину  линейного преобразования , производится с точностью до одного периода , задающего значение дискрета (кванта) измерения . Причем относительная ошибка преобразования  тем меньше, чем большее число периодов , в частности 2^m, укладывается в . В таблице 1.1 приведены соотношения ,  и m для преобразователей  и  в код  счетно-импульсного типа. Значения  даны для вариантов исполнения ПФИ на СИС (схемы со средним уровнем интеграции) и ПЛИС с тактовыми частотами 10 и 200 МГц соответственно.

Таблица 1.1

Значения погрешности , времени преобразования  и разрядности m линейных преобразователей  и

, %	0,1		0,025		0,0062		0,0016
m, бит	10		12		14		16
, МГц	10	200	10	200	10	200	10	200
, мс	0,1	0,005	0,4	0,02	1,6	0,08	6,6	0,3

Основу рассматриваемых математических моделей линейных преобразователей  прямого действия как кусочно-ступенчатых аппроксиматоров составляет формальный (или математический) нейрон (рис. 1.7).

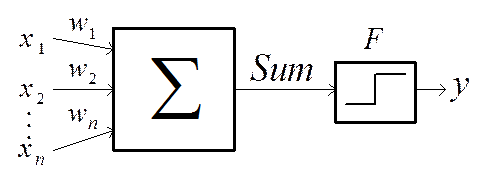
Рис. 1.7. Структура математического нейрона

Такой выбор обусловлен наличием в его результирующей фун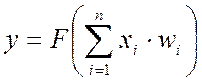кции  активационной функции  в виде зависимости релейного типа. По своей сути операция  может, в частности, интерпретироваться как однобитное аналого-цифровое преобразование. Нейрон (или нейроузел) состоит из суммирующего и порогового устройств. Суммирующий элемент суммирует получаемые взвешенные значения  для каждой входной переменной . Если эта сумма, т.е. 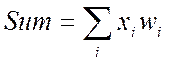, больше заданного порога, то значение переменной  на выходе порогового устройства нейрона равно одной дискретной величине, в противном случае – другой. Наряду с пороговой функцией активации, могут использоваться и другие виды оператора преобразования , выбираемые, в основном, в соответствии с решаемой задачей.

Путем целенаправленной настройки весов и порогов нейронов, объединенных в сеть, могут быть синтезированы нейросетевые структуры ПФИ, реализующих заданные операции преобразования. Однако при этом, в частности за счет неудачного выбора архитектуры сети или/и алгоритма ее обучения, могут быть получены модели преобразователя с избыточным количеством нейронов и связей между ними.

Наряду с этим, построение структуры преобразователя, называемой далее нейроподобной из-за схожести по своей конфигурации со схемой, образуемой в результате обучения ИНС, может также базироваться на использовании при вычислении аппроксимирующих функций операций формальных нейронов. Такое их применение позволяет в ряде случаев не только получить более простые (или альтернативные) для дальнейшей реализации модели преобразователей, но также сформулировать исходя из процесса их разработки определенные рекомендации по выбору архитектуры исходной нейросети и видов ее нейронов для создания ИНС-преобразователей с функцией обучения.

1.3.2. Основные методы получения функций включения  как значений пороговой бинарной функции активации нейрона