Нейросетевые преобразователи импульсно-аналоговых сигналов: Учебное пособие, страница 16

Следует отметить, что описание сугубо нейросетевой структуры преобразователя  может быть также сведено к виду (3.2), (3.3), если она обучена на реализацию операции линейного преобразования .

Этап 2. Задание логических сигналов нейроструктуры и ее нейроузлов с помощью матриц

Задание входных ,  и выходных ,  физических (машинных) переменных полученной на 1‑м этапе структуры ПФИ  и ее нейроузлов в виде матриц эквивалентных им логических (бинарных) сигналов является необходимой процедурой к переходу их описания в базисе логических операций. Такое представление возможно как на уровне всей структуры, так и на уровне ее отдельных узлов. При задании входов-выходов структуры ПФИ с помощью матриц вводится понятие степени однородности , характеризующей количество присутствующих в ней видов однородных нейроузлов (НУ). Под ними понимаются , реализующие одни и те же функционально-логические операции и имеющие одинаковое число входов и одинаковое число выходов. Так, например, для нейроструктуры (рис. 1.10,б), полностью состоящей из однородных узлов, параметр . Поэтому для  ее построение в булевом базисе сводится к проведению структурного синтеза только нейроузла .

Далее дан пример получения и матричного описания входных и выходных логических сигналов ПФИ  и его нейронов (рис. 1.10,б).

Матричное представлениеПФИ  на уровне всей структуры

Рассматриваемая модель ПФИ имеет степень однородности  и описывается с помощью полученной ранее совокупности зависимостей (3.2) и (3.3), а также в виде структуры, приведенной на рис. 1.10,б. Отображение ее входов-выходов с помощью матриц  и  соответственно имеет вид:

, .

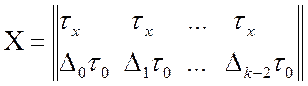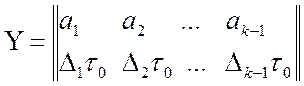Матричное представление преобразователя  на уровне отдельного нейрона

С помощью матричного исчисления ‑й нейроузел  структуры представляется в виде матриц  и , определяющих его входные ( и ) и выходные ( и ) математические переменные:

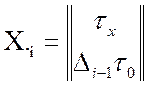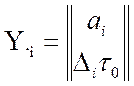,  .                                     (3.4)

Далее от (3.4) переходят к эквивалентным матрицам, определяющим входы-выходы  через бинарные (логические) сигналы, заданные для момента времени :

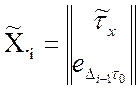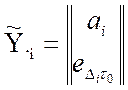,  .                                       (3.5)

При переходе от (3.4) к (3.5) аналоговые величины ,  и  заменяются на соответствующие им логические сигналы ,  и , отражающие двоичную логику формирования преобразуемых частотных и время-импульсных сигналов прямоугольной формы. Так, аналоговая величина, отражающая длительность  прямоугольных импульсов, следующих с периодом , заменяется логической переменной , которая описывает изменение  в пределах одного периода :

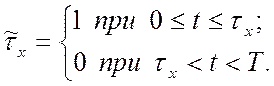                                          (3.6)

Величину  как дискрет преобразования  или , равный , предлагается отображать логической переменной  или , которая описывает поток единичных импульсов  опорной частоты , следующих с периодом  и равных единице в момент , :

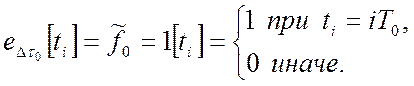                                (3.7)

Применение способа описания логических переменных в виде потока единичных импульсов (бит) для представления последовательности временных интервалов , а далее ,  и др. производится с учетом того, что , , .

С учетом этого переменные  и  при переходе к булевому базису операций представляются на отрезке времени  логическими сигналами  и , отражающими в нем моменты появления  единичных импульсов  частоты , начиная с момента  и  соответственно:

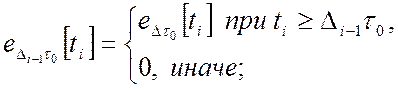                        (3.8)

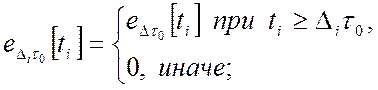                           (3.9)

где ; .

При построении логических схем нейросетевых структур необходимо осуществить переход от операций, заданных в нейросетевом базисе, к логическим операциям. В табл. 3.1 даны варианты перехода от ИНС‑операций к логическим для ряда рассмотренных ранее типов нейронов, с учетом единичных значений весов синаптических связей.

Таблица 3.1

Представление основных типов нейронов в логическом базисе

Тип нейрона	Вид функции активации	Вид входных сигналов	Вид выходных сигналов	Логическая схема
	Пороговая	D	D
	Пороговая	D	D
	Линейная
	Линейная
	Линейная

В табл. 3.1 введены следующие обозначения:  – цифровая переменная,  – временной интервал,  – частота,  и  – логические сигналы, отражающие логику формирования временного интервала и частоты соответственно.

Этап 3. Представление нейросетевых операций в булевом базисе, структурный синтез цифровых автоматов для их реализации

Выполнение данного этапа синтеза базируется на полученном математическом описании отдельных преобразователей, например  и , с применением операций нейросетевого функционально-логического базиса, а также матричном представлении их входов-выходов в виде логических сигналов. Все это позволяет далее получить операции, выполняемые ИНС-преобразователями, в булевом базисе, а затем осуществить структурный синтез цифровых устройств, реализующих эти операции.

Синтез ПФИ  (рис. 1.10,б) для формирования унитарного кода

Ввиду однородности своей структуры преобразователь  (рис. 1.10,б) можно декомпозировать на  одинаковых нейроузлов  (). На этапе структурного синтеза схему узла  целесообразно представить (рис. 3.1) в виде двух взаимосвязанных частей: памяти и комбинационной схемы (КС_i).

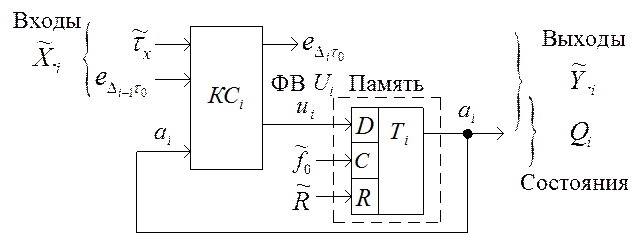
Рис. 3.1. Структурная схема  ПФИ  (рис. 1.10,б) как цифрового автомата (устройства)

Такое представление характерно для структурных автоматов (СА) Мили. В них память автомата строится из предварительно выбранных (или заданных) элементарных автоматов (ЭА), в качестве которых выступают триггеры определенного типа. Необходимость их применения в схеме  обусловлена тем, что формирование бит  (или ) кода  (или ), осуществляемое во времени , зависит от их предыдущих значений (за исключением число-импульсных кодов). В качестве ЭА обычно используются D‑триггеры, что во многом обусловлено их широким применением в микросхемах ПЛИС фирм Xilinx и Altera в качестве основного запоминающего элемента.