Нейросетевые преобразователи импульсно-аналоговых сигналов: Учебное пособие, страница 13

*  и  – число разрядов цифрового эквивалента для ПФИ  и .

2.3. Модели и процедуры синтеза структур ПФИ на базе многослойных персептронных сетей

2.3.1. Двухслойная персептронная модель структуры преобразователя , осуществляющего классификацию аналогового сигнала

Далее приводятся этапы синтеза нейросетевой модели преобразователя  с унитарным способом кодирования  в диапазоне , , …,  в виде:

,                                              (2.17)

где определенное (s+1)‑е положение единственного единичного бита  отражает значение преобразуемой аналоговой величины x, т.е.: , если , и  иначе; причем .

Данный пример иллюстрирует возможность применения предложенной методики синтеза для построения моделей преобразователей на основе двухслойной нейросети.

Выбор архитектуры сети

В основу построения модели преобразователя  с указанным способом кодирования  (2.17) положен двухслойный персептрон. Как видно из формулы (2.17), для нахождения значения , , требуется, в отличие от определения  (1.7), построить не одну, а две пороговые прямые (см. рис. 2.2,б), ограничивающие плоскость единичных значений  с двух сторон, что говорит о невозможности применения однослойного персептрона для формирования результата в виде (2.17). С учетом этого матричное описание исходной двухслойной персептронной сети примет вид:

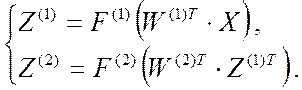
Ее аналитическое описание получается на основе (1.3), если принять число слоев :

, ,

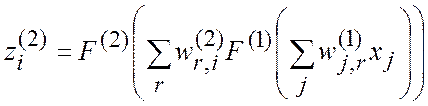где  и  – входные и выходные сигналы сети соответственно;

 и  – пороговые функции активации вида (2.3).

Определение базовой конфигурации структуры преобразователя как аппроксимирующей сети

Фиксированное размещение бит  в представлении унитарного кода  (2.17) приводит к тому, что матрица  выходных сигналов ИНС-аппроксиматора (как сети) должна учитывать местоположение бит , если . Поэтому матрица , изображенная в виде матрицы-столбца этих сигналов, будет отражать результат как упорядоченную последовательность бит  в виде  или .

Как уже отмечалось, при преобразовании  в качестве входных сигналов сети выступают преобразуемая величина  и эталон , например  (см. табл. 2.1). Поэтому число нейронов  ее входного слоя равно , а матрица  сети имеет вид (2.4).

В качестве выходных сигналов рассматриваемой сети (рис. 2.5) выступают значения бит  (), формируемые нейронами  выходного слоя, число которых =. Количество  нейронов скрытого слоя рекомендуется выбирать равным удвоенному числу нейронов выходного слоя. Операцию аналого-цифрового преобразования осуществляют нейроны  первого слоя. В связи с этим выходные сигналы  и  нейроузлов скрытого и выходного слоев представляются в виде двоичных значений бит, поэтому для их получения используются бинарные функции активации (2.3).

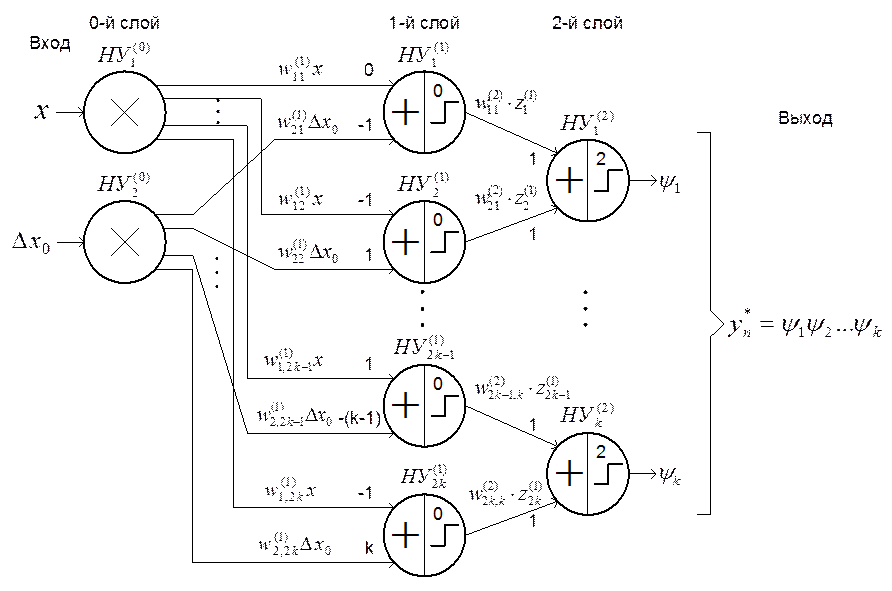
Рис. 2.5. Структура ИНС-преобразователя  на основе двухслойного персептрона

С учетом количества ,  и  нейронов, составляющих входной, скрытый и выходной слои соответственно, двухслойная персептронная сеть, реализующая операцию преобразования , описывается в виде системы:

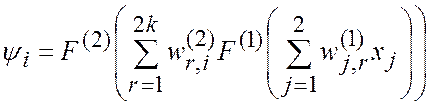, ,             (2.18)

где  – входная переменная, ;  – эталон преобразования , задаваемый в соответствии с табл. 1.1;

 и  – функции активации вида (2.3).

Зависимость (2.18) в матричной форме для всех бит эквивалента  примет вид:

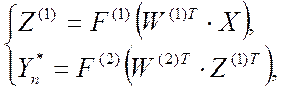                                         (2.19)

где  – матрица-строка, состоящая из входных аналоговых величин;

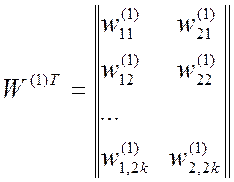 и  –

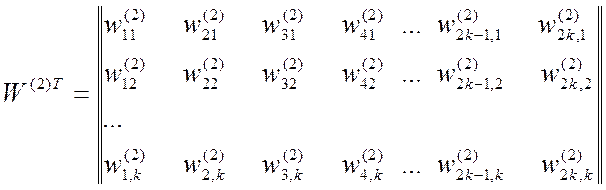транспонированные матрицы весовых коэффициентов между распределительным и скрытым, а также между скрытым и выходным слоями сети;

 – матрица-столбец, состоящая из бит эквивалента , образующих результат преобразования.

Нейросетевая модель преобразователя, реализующая аналитическую зависимость (2.18) с ее матричным представлением (2.19), показана на рис. 2.5. Время преобразования , затрачиваемое на формирование цифрового эквивалента , находится следующим образом:

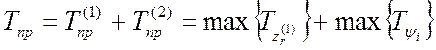,                            (2.20)

где  – время преобразования аналоговой переменной  в бит ;

 – время вычисления бита  на основе значений  ().

Время  в выражении (2.20) при аппаратной реализации 2‑го слоя определяется величиной времени задержки цифрового логического элемента, выполняющего нейрооперацию на выходном слое. Поэтому, учитывая что , выражение (2.20) можно переписать в виде:

.

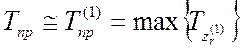Максимальная абсолютная погрешность  линейного преобразования определяется, как и в предыдущей модели, значением дискрета преобразования : . Так как относительная погрешность  преобразования  находится из выражения (1.13), то зависимость, связывающая  с числом  нейронов  выходного слоя, примет вид:

.                                                     (2.21)

Выражение (2.21) показывает, что относительная погрешность  преобразования  обратно пропорциональна числу  нейронов  выходного слоя.

Обучение сети

Обучение персептрона со скрытыми слоями целесообразно осуществлять с использованием алгоритма обратного распространения ошибки. С целью настройки синаптических связей он использует метод градиентного спуска в пространстве весовых коэффициентов и порогов нейронной сети. Для задачи преобразования аналоговой величины x в ее цифровой эквивалент (2.17) полученные в результате обучения 2-слойной сети значения весов ее синаптических связей показаны на рис. 2.5, а также представлены матрицам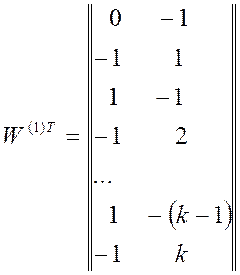и:

 и 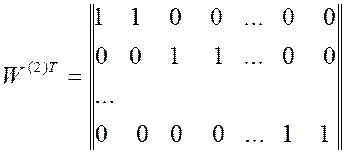 .           (2.22)

C учетом полученных при обучении сети весов (2.22) и порогов  и  на основе (2.19) можно сформировать системы бинарных активационных функций  и , реализуемых нейронами:

1-го слоя:

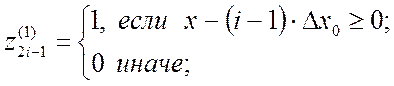
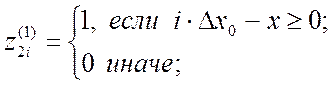            (2.23)

2-го слоя:

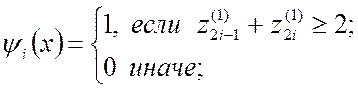
 .                                      (2.24)

Поскольку сигналы  и  являются однобитными переменными, то зависимость (2.24), реализуемая i‑м нейроном 2-го слоя сети (рис. 2.5), тождественна логической операции "И" над  и . Значения составляющих параметров n, V и структуры нейросети (рис. 2.5) даны в табл. 2.2.