Линейное программирование: Рабочая программа, контрольные работы и учебное пособие

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

РЯЗАНСКАЯ ГОСУДАРСТВЕННАЯ РАДИОТЕХНИЧЕСКАЯ АКАДЕМИЯ

А.И. НОВИКОВ,  М.Е. ИЛЬИН,

Т.В. ДОВЖИК,  Н.В. ЕЛКИНА

ЛИНЕЙНОЕ

ПРОГРАММИРОВАНИЕ

Рязань 2006 Федеральное агентство по образованию

Рязанская государственная радиотехническая академия

А.И. НОВИКОВ,  М.Е. ИЛЬИН,

Т.В. ДОВЖИК,  Н.В. ЕЛКИНА

ЛИНЕЙНОЕ

ПРОГРАММИРОВАНИЕ

Учебное пособие

Допущено Учебно-методическим объединением по образованию в области производственного менеджмента в качестве учебного пособия для студентов, обучающихся по специальности 080502 «Экономика и управление на предприятии машиностроения»

Рязань 2006

УДК 512.25

Линейное программирование: Учеб. пособие /А.И.Новиков, М.Е. Ильин, Т.В. Довжик, Н.В. Ёлкина. Под ред. Ю.М. Солдака; Рязан. гос. радиотехн. акад. Рязань, 2006. 96 c. ISBN 5-77-22-0265-0

Содержит рабочую программу, контрольные работы и собственно учебное пособие по одноименному курсу (пятый раздел).

Предназначено для студентов специальности 080502 «Экономика и управление на предприятии машиностроения»

Табл. 11. Ил. 9. Библиогр.: 5 назв.

Целевая функция, множество допустимых решений, графические методы, симплекс-алгоритм, транспортная задача

Печатается по решению редакционно-издательского совета Рязанской государственной радиотехнической академии.

Рецензент: кафедра высшей математики РГРТА (зам. зав. кафедрой доц., канд. физ.-мат. наук М.Е. Ильин).

Н о в и к о в Анатолий Иванович

И л ь и н Михаил Евгеньевич

Д о в ж и к Татьяна Владимировна

Е л к и н а Наталия Викторовна

Линейное программирование

Редактор  Р.К. Мангутова

Корректор  С.В. Макушина

Подписано в печать 06.03.06. Формат бумаги 60´84 1/16.

Усл. печ. л. 6,0.

Уч.-изд. л. 6,0. Тираж 150 экз. Заказ

Рязанская государственная радиотехническая академия.

390005, Рязань, ул. Гагарина, 59/1.

Редакционно-издательский центр РГРТА.

ISBN    5-7722-0265-0

Ó

Рязанская государственная радиотехническая академия, 2006

1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1.1.   Математические модели экономических задач

Математическое программирование – это раздел математики, изучающий методы нахождения экстремумов функций многих переменных при дополнительных ограничениях на множество допустимых значений этих переменных в виде уравнений и неравенств. Составными частями математического программирования являются линейное, нелинейное и динамическое программирование.

Математическое программирование получило распространение как инструмент исследования экстремальных экономических задач. Исследование экономических процессов обычно начинается с составления их математических моделей, т.е. совокупности математических соотношений, описывающих исследуемый экономический процесс. Рассмотрим содержательные примеры некоторых задач математического программирования.

Задача использования ресурсов

Для изготовления n видов продукции  используют m видов ресурсов . Это могут быть металл, электроэнергия, различные поставки с других предприятий и т.п. Объем каждого ресурса ограничен и известен . Известно также   – количество каждого i-го вида ресурса, расходуемого на производство единицы j-го вида продукции. Кроме того, известна прибыль, получаемая от реализации единицы каждого вида продукции .

Условия задачи можно представить в виде табл. 1.1.

Таблица 1.1

Объем ресурсов	Количество единиц ресурса, идущих на изготовление единицы продукции
			…
			…
			…
…	…	…	…	…
			…
Прибыль			…

Пусть  – количество каждого вида продукции, которое может быть произведено при заданных условиях. Тогда для 1-го ресурса можно составить неравенство-ограничение

.

Аналогичные неравенства будут иметь место и для остальных видов ресурсов.

Общая прибыль, получаемая от реализации всей продукции, будет линейной функцией:

,    .

Тогда математическая модель этой задачи может быть записана в виде:

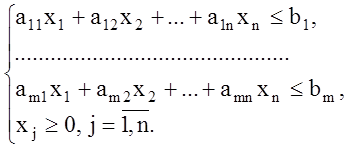
Задача о составлении рациона питания

Требуется составить ежедневный рацион питания животного на основе имеющихся видов кормов так, чтобы общая стоимость использованных кормов была минимальной.

Пусть имеется n видов кормов , которые содержат в различных количествах m видов питательных веществ ; это могут быть жиры, углеводы, белки, витамины и т.п.

Обозначим через  содержание (в весовых единицах) i-го питательного вещества в единице j-го корма, а через  –минимальную суточную потребность животного в i-м питательном веществе; через  – количество каждого вида корма в ежедневном рационе ();  – стоимость весовой единицы j-го корма.

Математическая модель данной задачи имеет вид:

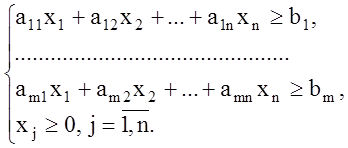
1.2. Основные формы записи задач

линейного программирования

Несмотря на различия содержательных ситуаций, соответствующие им экстремальные математические задачи имеют много общего: в каждой нужно минимизировать или максимизировать линейную функцию нескольких переменных; ограничения, наложенные на переменные, являются линейными уравнениями или неравенствами.

Различаются три основные формы задач линейного программирования.

1. Стандартная (основная) задача линейного программирования.

Задача ЛП называется стандартной или основной задачей, если все функциональные соотношения, определяющие допустимое множество решений, являются неравенствами.

           (1.1)

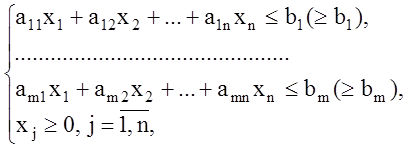                 (1.2)

или в матричной записи

                         (1.3)

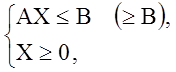                                      (1.4)

где       ,

,

,

.

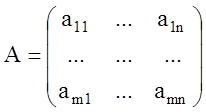2. Каноническая задача линейного программирования

           (1.5)

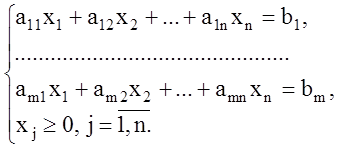                   (1.6)

Таким образом, в канонической задаче ЛП допустимое множество решений задается системой уравнений.

3. Общая задача линейного программирования.

        (1.7)

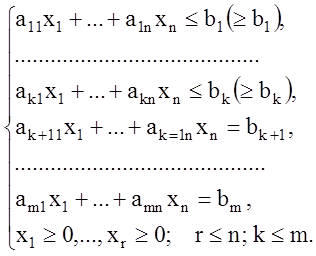                   (1.8)

Если , , то получается стандартная задача линейного программирования; если , , то получается каноническая задача.

Определение 1.1. Величины , характеризующие экономический процесс, называются переменными задачи.

Определение 1.2. Линейная функция

,

которую нужно максимизировать или минимизировать, называется целевой функцией.

Определение 1.3. Вектор  называется вектором коэффициентов целевой функции,

матрица 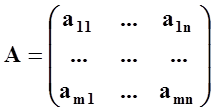 – матрицей условий,

а вектор  – вектором ограничений.

Так как целевая функция линейна и ограничения линейны, то задачи (1.1), (1.2); (1.5), (1.6); (1.7), (1.8) называются задачами линейного программирования.

Определение 1.4. Вектор X, удовлетворяющий всем ограничениям задачи, называется допустимым вектором или допустимым планом.

Определение 1.5. Задача линейного программирования, для которой множество допустимых планов не пусто, называется допустимой задачей.

Определение 1.6. Допустимый план, максимизирующий или минимизирующий целевую функцию, называется оптимальным.

1.3. Приведение одной формы задачи