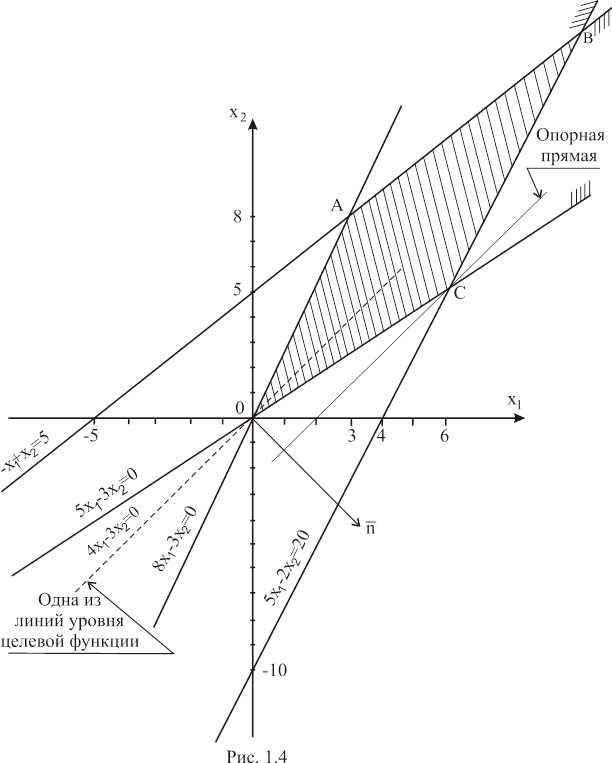
Подставляя координаты точки C (6;5) в целевую функцию, получаем решение задачи:
![]() .
.
Ответ: ![]() при
при ![]() .
.
1.5. Выпуклые множества
 Пусть на плоскости
Пусть на плоскости ![]() заданы точки
заданы точки ![]() и
и
![]() , определяющие отрезок
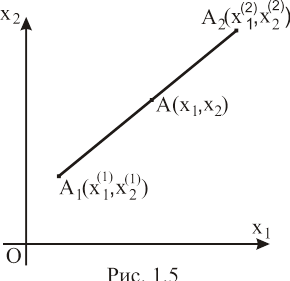
, определяющие отрезок ![]() (рис. 1.5). Найдем координаты произвольной
точки
(рис. 1.5). Найдем координаты произвольной
точки ![]() данного отрезка, т.е. выразим их
через координаты концов отрезка. Так как векторы
данного отрезка, т.е. выразим их
через координаты концов отрезка. Так как векторы ![]() и
и
![]() коллинеарны, то
коллинеарны, то ![]() , где
, где ![]() или
или
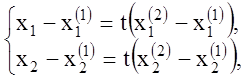
отсюда
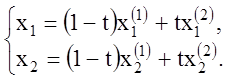
Полагая ![]() ,
, ![]() ,
получаем
,
получаем
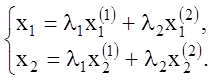 (1.12)
(1.12)
![]() ,
, ![]() ,
, ![]() .
.
Учитывая, что в (5.12) координаты точки A
являются суммами одноименных координат точек ![]() и
и
![]() , умноженными соответственно на
, умноженными соответственно на ![]() ,
, ![]() ,
окончательно получаем
,
окончательно получаем
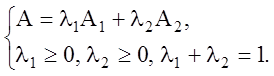 (1.13)
(1.13)
Определение 1.10. Точка A
является выпуклой линейной комбинацией точек ![]() и
и
![]() , если для нее выполняются условия
(1.13).
, если для нее выполняются условия
(1.13).
Определение 1.11. В общем
случае, точка A является выпуклой линейной комбинацией точек ![]() , если для нее выполняются условия
, если для нее выполняются условия
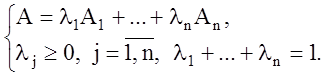 (1.14)
(1.14)
Определение 1.12. Множество называется выпуклым, если оно содержит выпуклую линейную комбинацию любых своих точек.
Геометрически это означает, что если две точки принадлежат множеству, то и отрезок, соединяющий эти точки, принадлежит этому множеству.
Примерами выпуклых множеств служат отрезок, полуплоскость, многоугольник, круг, полупространство, куб и др.
Определение 1.13. Точка множества называется граничной, если любая окрестность данной точки содержит как точки, принадлежащие множеству, так и точки, не принадлежащие множеству.
Определение 1.14. Множество называется замкнутым, если оно содержит все свои граничные точки.
Определение 1.15. Множество называется ограниченным, если ![]() такое, что шар радиусом R
с центром в любой точке данного множества полностью содержит это множество.
такое, что шар радиусом R
с центром в любой точке данного множества полностью содержит это множество.
Определение 1.16. Угловой точкой выпуклого множества называется точка, не являющаяся выпуклой линейной комбинацией каких-либо различных точек этого множества.
Множество может иметь любое число угловых точек: одну (рис. 1.6, а), две (рис. 1.6, б), три (рис. 1.6, в) и т.д., а также бесконечное число угловых точек (рис. 1.6, г).
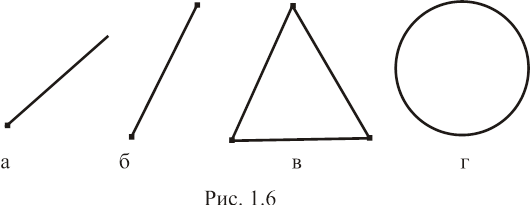
Множество может и не иметь угловых точек, например прямая, полуплоскость и т.д.
Определение 1.17. Многогранником называется выпуклое, замкнутое, ограниченное множество, имеющее конечное число угловых точек.
1.6. Свойства решений задач
линейного программирования
Рассмотрим задачу
![]() (1.15)
(1.15)
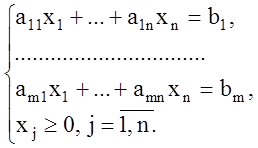 (1.16)
(1.16)
Приведённые ниже теоремы 1.2-1.5 определяют свойства допустимого множества решений и целевой функции на множестве допустимых планов.
Теорема 1.2. Множество допустимых планов задачи (1.15), (1.16) является выпуклым множеством.
Теорема 1.3. Целевая функция задачи (1.15), (1.16) достигает экстремума в угловой точке множества допустимых планов. Если целевая функция достигает экстремума в нескольких угловых точках, то она достигает экстремума в любой выпуклой линейной комбинации этих точек.
Введем обозначения.
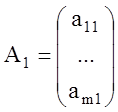 ,…,
,…,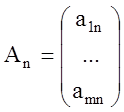 – это векторы условий, тогда система
ограничений (1.16) в векторной записи имеет вид:
– это векторы условий, тогда система
ограничений (1.16) в векторной записи имеет вид:
![]() .
(1.17)
.
(1.17)
Теорема 1.4. Если система векторов условий ![]()
![]() линейно
независима и такова, что
линейно
независима и такова, что
![]() ,
,
где ![]() , то
, то ![]() – угловая точка множества решений
системы ограничений.
– угловая точка множества решений
системы ограничений.
Теорема 1.5. Если ![]() –
угловая точка множества решений системы ограничений, то векторы условий
–
угловая точка множества решений системы ограничений, то векторы условий ![]() , соответствующие положительным
координатам
, соответствующие положительным
координатам ![]() , являются линейно независимыми.
, являются линейно независимыми.
Определение 1.18. Опорным планом (решением) задачи линейного программирования называется допустимый план, для которого векторы условий, соответствующие его положительным координатам, линейно независимы.
Из теорем 1.4 и 1.5 следует, что угловые точки множества решений системы ограничений являются опорными планами.
Определение 1.19. Если отличных от нуля координат опорного плана m, то план называется невырожденным, если меньше m – вырожденным.
Определение 1.20. Базисом опорного плана называется базис системы векторов условий, в состав которого входят векторы, соответствующие отличным от нуля координатам опорного плана.
Из приведенных выше теорем 1.2 – 1.5 следует, что оптимальное решение задачи линейного программирования (1.15), (1.16) нужно искать среди угловых точек множества допустимых планов. В связи с этим возникают следующие вопросы:
- как найти начальный план?
- как перейти от начального опорного плана к новому (от одной угловой точки многогранника решений к другой)?
- как оценить изменение целевой функции при переходе от одного опорного плана к другому?
- как определить окончание процесса перебора угловых точек: либо потому, что найдено оптимальное решение, либо потому, что такое решение не существует, т.е. каковы условия оптимальности опорного плана?
Ответы на эти вопросы даны в следующем разделе 1.7.
1.7. Построение опорных планов
Процесс построения начального опорного плана, последующего
перехода к новому (лучшему) опорному плану рассмотрим на примере задачи ЛП с
пятью переменными ![]() и тремя уравнениями
и тремя уравнениями ![]() в системе ограничений. При этом на первом
этапе будем считать, что в каждое уравнение системы ограничений и только в него
входит переменная
в системе ограничений. При этом на первом
этапе будем считать, что в каждое уравнение системы ограничений и только в него
входит переменная ![]() с коэффициентом
с коэффициентом ![]() .
.
1.7.1.Построение начального опорного плана
Будем рассматривать задачу
![]() (1.18)
(1.18)
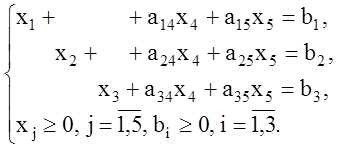 (1.19)
(1.19)
Система уравнений (1.19) содержит три единичных вектора
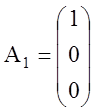 ,
, 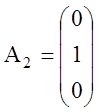 ,
, 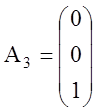 .
.
Они образуют базис в системе
векторов ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
В соответствии с общей схемой решения неопределенных
СЛАУ объявляем переменные ![]() ,
, ![]() ,
, ![]() базисными,
а
базисными,
а ![]() ,
, ![]() –
свободными и полагаем
–
свободными и полагаем ![]() ,
, ![]() .
Тогда СЛАУ (1.19) примет следующий вид:
.
Тогда СЛАУ (1.19) примет следующий вид:
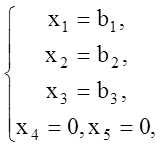
а
решением СЛАУ будет вектор ![]() . Полученный план
. Полученный план
![]() будет допустимым планом, так как его
положительным координатам соответствуют линейно независимые векторы
будет допустимым планом, так как его
положительным координатам соответствуют линейно независимые векторы ![]() ,
, ![]() ,
, ![]() и
и
![]() .
.
Построенный начальный опорный план
доставляет целевой функции ![]() значение
значение
![]() .
.
Рассмотрим конкретный пример
Пример 1.4. Решить задачу ЛП.
![]() (1.20)
(1.20)
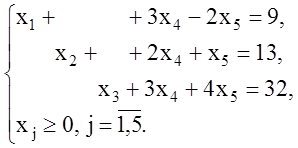 (1.21)
(1.21)
Решение.
1. Выбор начального опорного плана
Множество допустимых планов задачи определяется системой линейных уравнений (1.21). Эту систему можно переписать в векторной форме
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.