Линейное программирование: Рабочая программа, контрольные работы и учебное пособие, страница 12

Опорное решение  будет оптимальным, если  при , то есть в свободных клетках нет положительных оценок . Найдем оценки свободных клеток:

,

,

,

,

,

.

Так как , то найденное опорное решение  не является оптимальным, поэтому нужно перейти к новому опорному решению, на котором значение целевой функции будет меньше найденного . Для этого находим клетку, которой соответствует наибольшая положительная оценка. В данном случае такая клетка только одна, поэтому . Затем строим цикл, включающий в свой состав клетку (1, 2) и часть клеток, занятых опорным решением . Для этого вычеркиваем те строки и  столбцы, которые содержат одну занятую клетку (это третья строка и третий и четвертый столбцы). Оставшиеся занятые клетки и составляют цикл.

В клетках цикла расставим поочередно знаки  и  начиная с  в клетке (1,2) с наибольшей положительной оценкой. Внутри цикла осуществляют сдвиг (перераспределение груза) на величину . Клетка со знаком , в которой достигается 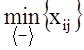, остается пустой. В данном примере цикл следующий:

	45		15			20		20
25		9			5		3		10
	5					20
			1
55		6			3		8		2
	20		15					20
20		3			8		4		8
	20

Сдвиг осуществляем на величину  и получаем новое опорное решение :

	45		15		20		20
25		9		5		3		10
			5		20
55		6		3		8		2
	25		10				20
20		3		8		4		8
	20

Полученное опорное решение 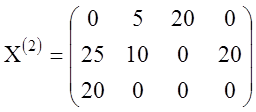 нужно проверить на оптимальность. Для этого строим новую систему потенциалов, решая систему уравнений:

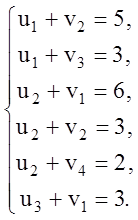
Полагая , последовательно находим: , , , ,  и . Найдем оценки свободных клеток:

,

,

,

,

,

.

Так как среди оценок нет положительных, то найденное опорное решение  будет являться оптимальным. Значит, наименьшее значение  целевой функции равно:

.

Ответ: .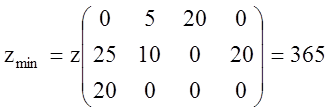

3. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

Задача 1

Решить графически задачу линейного программирования с двумя переменными.

1.	2.
3.	4.
5.	6.

7.	8.
9.	10.
11.	12.

13.	14.
15.	16.
17.	18.

19.	20.
21.	22.
23.	24.

25.	26.
27.	28.
29.	30.
31.	32.
33.	34.
35.	36.
37.	38.
39.	40.

Задача 2

Решить задачу линейного программирования симплекс-методом.

1.	2.
3.	4.
5.	6.

7.	8.
9.	10.
11.	12.
13.	14.

15.	16.
17.	18.
19.	20.
21.	22.

23.	24.
25.	26.
27.	28.
29.	30.

31.	32.
33.	34.
35.	36.
37.	38.

39.

40.

Задача 3

Для данной  канонической задачи линейного программирования составить двойственную, решить ее графически и, используя теорему двойственности, найти решение исходной задачи.

1.	2.
3.	4.

5.	6.
7.	8.
9.	10.
11.	12.

13.	14.
15.	16.
17.	18.
19.	20.

21.	22.
23.	24.
25.	26.
27.	28.

29.	30.
31.	32.
33.	34.
35.	36.

37.	38.
39.	40.

Задача 4

Решить транспортную задачу линейного программирования методом потенциалов (начальный опорный план находить методом «северо-западного» угла).