линейного программирования к другой
1. Приведение к канонической задаче линейного программирования
В канонической
задаче все условия системы ограничений являются уравнениями и все переменные
неотрицательные. Однако при составлении математических моделей реальных экономических
задач ограничения в основном имеют вид неравенств, поэтому необходимо уметь
переходить от системы неравенств к системе уравнений. Это можно сделать
следующим образом: вводятся неотрицательные вспомогательные переменные, для
каждого неравенства своя переменная. В целевую функцию вспомогательные
переменные включают с нулевыми коэффициентами. Если левая часть неравенства
связана с правой неравенством ![]() , то
вспомогательная переменная прибавляется к левой части; если же неравенство
имеет вид
, то
вспомогательная переменная прибавляется к левой части; если же неравенство
имеет вид ![]() , то вспомогательная переменная
вычитается из левой части.
, то вспомогательная переменная
вычитается из левой части.
Пример 1.1. Привести задачу к канонической форме.
![]()
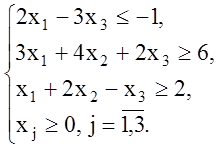
Решение.
Неравенств в задаче три, поэтому вводятся три вспомогательные неотрицательные
переменные ![]() ,
, ![]() ,
, ![]() . К левой части 1-го неравенства
нужно добавить вспомогательную переменную
. К левой части 1-го неравенства
нужно добавить вспомогательную переменную ![]() ,
а из левой части 2-го и 3-го неравенств вычесть соответствующие вспомогательные
переменные
,
а из левой части 2-го и 3-го неравенств вычесть соответствующие вспомогательные
переменные ![]() и
и ![]() .
Получим каноническую задачу
.
Получим каноническую задачу
![]()
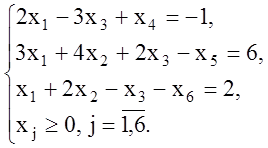
2. Приведение к стандартной форме задачи линейного программирования
Пример 1.2. Привести каноническую задачу ЛП к стандартной форме
![]()
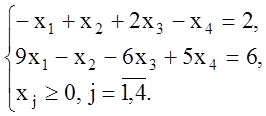
Решение. Методом Гаусса-Жордана приведем систему уравнений-ограничений задачи к равносильной разрешенной. Одновременно разрешенные переменные исключим из целевой функции. Для этого в расширенную матрицу системы ограничений запишем дополнительную строку коэффициентов целевой функции. В последнем столбце дополнительной строки запишем свободный член целевой функции, равный нулю. При вычислении учитываем, что разрешающий элемент в последней строке выбирать нельзя. Получаем:
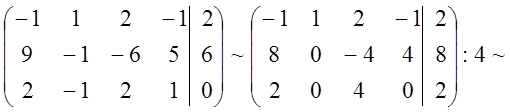
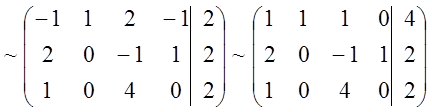 .
.
В результате данных преобразований задача принимает следующий вид:
![]()
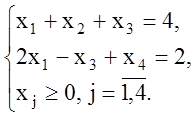
Число
2, полученное в последнем столбце дополнительной строки, записываем в целевую
функцию с противоположным знаком. Так как переменные ![]() и
и
![]() неотрицательные, то, отбросив их,
можно записать задачу в стандартном виде:
неотрицательные, то, отбросив их,
можно записать задачу в стандартном виде:
![]()
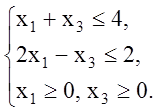
1.4. Графический метод решения задач
линейного программирования
Графический метод используется для решения задач с двумя переменными.
Рассмотрим задачу:
![]() (1.9)
(1.9)
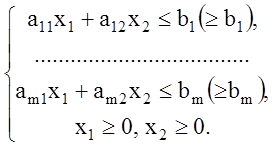 (1.10)
(1.10)
Данный метод основывается на возможности графического изображения области допустимых решений задачи и линии уровня целевой функции.
Каждое неравенство системы ограничений определяет одну
из двух полуплоскостей, на которые прямая ![]() делит
всю плоскость. Чтобы выбрать полуплоскость, достаточно координаты какой-либо
точки, не лежащей на прямой, подставить в соответствующее неравенство: если оно
выполняется, то выбирается та полуплоскость, которой принадлежит данная точка;
если оно не выполняется, то выбирается полуплоскость, которой не принадлежит
данная точка.
делит
всю плоскость. Чтобы выбрать полуплоскость, достаточно координаты какой-либо
точки, не лежащей на прямой, подставить в соответствующее неравенство: если оно
выполняется, то выбирается та полуплоскость, которой принадлежит данная точка;
если оно не выполняется, то выбирается полуплоскость, которой не принадлежит
данная точка.
Определение 1.7. Пересечение всех полуплоскостей – это некоторая многоугольная область D (множество допустимых векторов-планов), которая называется многоугольником решений системы ограничений.
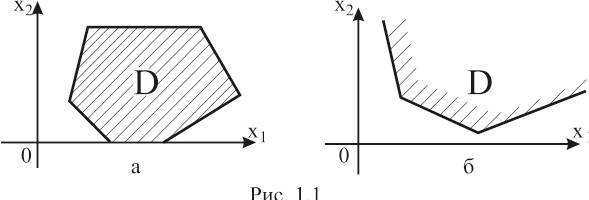
На рис. 1.1,а,б представлены некоторые возможные многоугольники решений системы ограничений.
Возможен случай, когда D – пусто, т.е. нет ни одной точки, удовлетворяющей всем неравенствам системы одновременно.
Для нахождения среди допустимых решений оптимального используют линии уровня и опорные прямые.
Определение 1.8. Линией уровня линейной целевой функции называется прямая, на которой целевая функция задачи принимает постоянное значение. Уравнение линии уровня в общем случае имеет вид
![]() ,
(1.11)
,
(1.11)
где c – сonst.
Все линии уровня параллельны между собой.
Определение 1.9. Опорной прямой называется линия уровня, имеющая хотя бы одну общую точку с многоугольником решений системы ограничений D, и по отношению к которой D находится по одну сторону.
Область D имеет не более двух опорных прямых (см. рис.1.2,а,б).
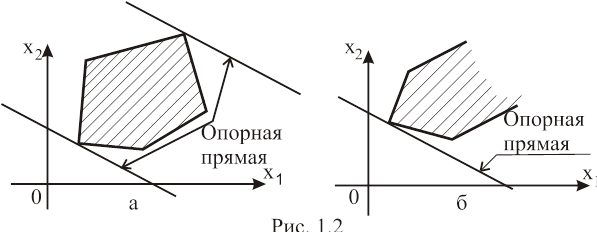
Любая из точек пересечения опорной прямой и многоугольника решений системы ограничений D является допустимым решением задачи.
Вектор градиента целевой функции
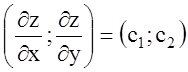
является вектором нормали любой прямой
![]() (линии уровня целевой функции).
(линии уровня целевой функции).
Известно, что вектор градиента функции указывает направление наискорейшего возрастания этой функции, что позволяет сформулировать теорему.
Теорема 1.1. Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении вектора нормали, и убывают при перемещении в противоположном направлении.
Таким образом, приходим к следующему алгоритму решения задачи графическим методом.
1. Строим многоугольник решений системы ограничений.
2. Строим некоторую линию
уровня для выбранного значения с (![]() ) и нормаль линии
уровня
) и нормаль линии
уровня ![]() .
.
3. Перемещаем линию уровня в задаче на максимум в направлении вектора нормали, в задаче на минимум - в противоположном направлении до положения опорной прямой.
4. Находим точки пересечения опорной прямой и многоугольника решений системы ограничений.
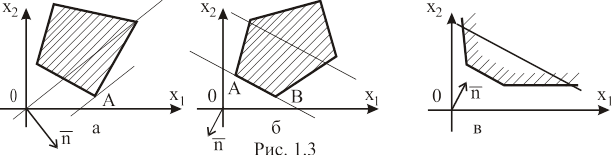
Задача может иметь единственное решение (рис. 1.3, а, точка A), бесконечное множество решений (рис. 1.3, б, точки отрезка AB) или не иметь ни одного (рис. 1.3, в).
Пример 1.3. Решить графически задачу ЛП.
![]()
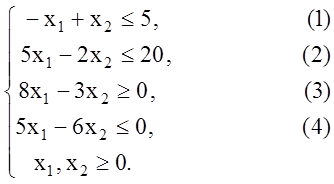
Решение.
Строим многоугольник решений системы
ограничений. Проводим прямую ![]() (1). Выбираем
полуплоскость, определяемую неравенством
(1). Выбираем
полуплоскость, определяемую неравенством ![]() .
Для этого возьмем точку (0;0) и подставим ее координаты в левую часть
неравенства. Получим верное неравенство
.
Для этого возьмем точку (0;0) и подставим ее координаты в левую часть
неравенства. Получим верное неравенство ![]() ,
следовательно, точка (0;0) лежит в полуплоскости решений. Аналогично строим прямые
,
следовательно, точка (0;0) лежит в полуплоскости решений. Аналогично строим прямые
![]() (2),
(2), ![]() (3),
(3),
![]() (4) и выбираем полуплоскости. В
результате получим многоугольник OABC (рис. 1.4). Строим одну из линий уровня, например
(4) и выбираем полуплоскости. В
результате получим многоугольник OABC (рис. 1.4). Строим одну из линий уровня, например ![]() , и вектор нормали к ней
, и вектор нормали к ней ![]() .
.
Так как задача на максимум, перемещаем прямую параллельно самой себе в направлении вектора нормали, находим опорную прямую.
Решением задачи является
точка C – точка пересечения прямых ![]() и
и ![]() (рис.
1.4). Находим ее координаты, решая систему:
(рис.
1.4). Находим ее координаты, решая систему:
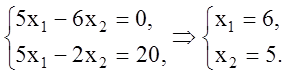
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.