Линейное программирование: Рабочая программа, контрольные работы и учебное пособие, страница 5

вычисляется как сумма произведений элементов 1-го столбца на 2-й минус . Аналогично

.

Значение целевой функции

записывается в ячейке, отвечающей последней строке и последнему столбцу матрицы.

Пример 1.4. (продолжение решения)

2. Выбор нового опорного плана

Из матрицы (1.33) следует, что  и . Это означает, что если в базис  ввести вектор  или вектор  вместо соответствующего вектора старого базиса, то значение целевой функции увеличится. Напомним, что в примере 1.4 решается задача максимизации.

Выясним теперь, введение в базис какого вектора ( или ) даст наибольшее увеличение целевой функции. Для этого, как следует из (1.30), нужно вычислить абсолютное увеличение (в задаче максимизации) или уменьшение (в задаче минимизации):

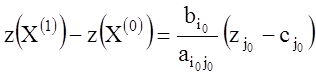.                  (1.34)

Здесь  – номер вводимого в базис вектора,  – номер выводимого.

Пусть , т.е. вводится . В этом случае, как уже установлено

,

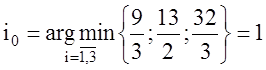а это означает, что вывести из базиса нужно вектор . В соответствии с (1.34)

,

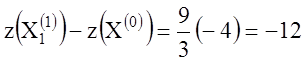т.е. значение целевой функции  на плане  увеличится на двенадцать единиц по сравнению с начальным опорным планом и составит

.

Пусть теперь . Тогда

,

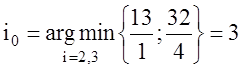т.е. вектор  должен вводиться в базис вместо . Вычислим теперь изменение целевой функции:

,

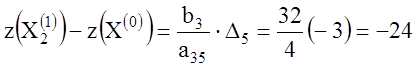т.е. введение в базис вектора  вместо вектора  приведем к увеличению целевой функции на 24 ед. Поскольку , то

.

Можно сделать следующий вывод: для получения лучшего нового опорного плана, по сравнению с опорным планом , нужно в старый базис  ввести вектор , а вывести . Это эквивалентно тому, что соответствующим образом изменяются совокупности базисных переменных (вместо , ,  ими будут теперь , , ) и свободных (,  вместо , ).

С вычислительной точки зрения переход к новому базису сводится к построению новой таблицы (матрицы) (1.33). В этой таблице первый столбец теперь будет иметь вид , а все строки, кроме первой и последней, преобразуются с помощью элементарных преобразований над строками так, чтобы в шестом столбце получился единичный вектор . Для этого:

-  все элементы четвертой строки, кроме элемента первого столбца, в (1.33) делим на 4;

-  из третьей строки вычитаем четвертую;

-  ко второй строке прибавляем четвертую, умноженную на 2.

В результате этих преобразований получим таблицу

. (1.35)

Значение  в последней строке таблицы (1.35) вычислялось, как и прежде по формуле (1.32). В последнем столбце таблицы (1.35) получены значения базисных переменных: , , . Соответственно  – новый опорный план, а  – значение целевой функции на этом плане.

Слева от таблицы (1.35) указаны номера базисных переменных. Для удобства записи их целесообразно включить в таблицу в качестве первого столбца.

Проанализируем таблицу (1.35). В последней строке таблицы (со значениями ) 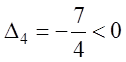, а элементы , , вектора  в этом столбце положительны. Это означает, что введение в базис  вектора  приведет к получению нового лучшего опорного плана .

Найдем номер вектора, который необходимо вывести из базиса :

,

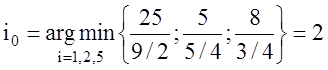т.е. вектор  должен вводиться в базис вместо вектора .

Новая таблица (1.36) строится аналогично (1.35). Дополнительно в нее вводим первый столбец номеров базисных переменных . Вектор C коэффициентов  целевой функции, отвечающих базисным переменным, будет иметь вид . Элементы второй, третьей и четвертой строк таблицы (1.35) преобразуются так, чтобы в пятом столбце получился единичный вектор :

. (1.36)

В последней строке таблицы (1.36) все величины  неотрицательны. Это означает, что улучшить план нельзя и значение  целевой функции является оптимальным.

Ответ:  ; .

Комментарий к примеру 1.4

Если исключить промежуточные вычисления [формулы (1.28), (1.32)] и процедуры выбора базисных и свободных переменных при построении каждого нового опорного плана, то все решение примера 1.4 (и любой другой задачи ЛП) сводится к последовательному построению таблиц (1.33), (1.35), (1.36). В этих таблицах содержится вся информация о решении задачи ЛП (о цепочке опорных планов ). Традиционно решение учебных примеров оформляют в виде специальных симплекс-таблиц (см. раздел 1.9, табл. 1.2), которые в значительной мере повторяют по структуре таблицу 1.36.

1.8. Условия оптимальности опорного плана

Результаты, полученные в разделе 1.7 для частных значений n и m (, ), позволяют сделать некоторые важные выводы для произвольных значений n и m.

Рассмотрим вновь каноническую задачу (1.15), (1.16). Допустим, что с помощью равносильных преобразований система уравнений связи (1.16) приведена к виду (1.19)

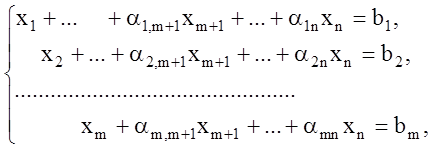         (1.37)

или ,

здесь 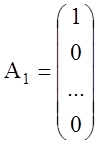, ,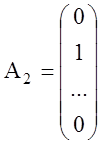…, 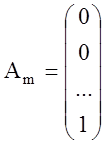– базисные векторы.

В задаче ЛП

                  

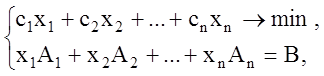
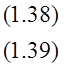
в качестве начального опорного плана можно взять точку

.

Тогда  – значение целевой функции на данном плане.

Переход от начального опорного плана  к другому (другим) будет приводить к изменению значения целевой функции. Для оценивания этих изменений в соответствии с результатами пункта 1.7.3 [см. (1.23), (1.24)] нужно вычислить величины

, ,           (1.40)

где  – компоненты вектора  или координаты разложения вектора  по базису :

.

Затем вычисляем величины

, .                          (1.41)

Они дают количественную оценку (см. (1.23)) изменения целевой функции  при введении в базис вектора . Отметим, что  для . Действительно, например, при

и потому .

Если среди , , есть положительные величины, то введение в базис соответствующего вектора  приведет к уменьшению значения целевой функции [см. (1.23), (1.24)]. Если же  для всех , то план  улучшить нельзя.

Эти выводы составляют условия оптимальности.

Теорема 1.6 (для задачи на минимум). Если для некоторого вектора , не входящего в базис, выполняется условие , то план  не является оптимальным и можно построить план  такой, что . Если же  для всех , то план  – оптимальный.

Условия оптимальности в задаче ЛП на максимум формируются аналогично.

Теорема 1.7 (для задачи на максимум). Если для некоторого вектора , не входящего в базис, выполняется условие , то план  не является оптимальным и можно построить план  такой, что . Если же  для всех , то план  – оптимальный.