Линейное программирование: Рабочая программа, контрольные работы и учебное пособие, страница 9

Выбираем в табл. 1.6 наименьшую стоимость перевозки, это стоимость 1, помещенная в клетки (1,2) и (2,3). Так как , то помещаем в клетку (1,2) 80, и так как запасы 1-го поставщика все израсходованы, то в остальных клетках 1-й строки ставим прочерк. Так как потребности 2-го потребителя удовлетворены, то в остальных клетках 2-го столбца ставим прочерк. Сравниваем запасы 2-го поставщика и 3-го потребителя: , поэтому в клетку (2,3) ставим 90, так как потребности 3-го потребителя удовлетворены, то в остальных клетках третьего столбца ставим прочерк. У 2-го поставщика осталось ед. груза. В оставшейся таблице минимальной стоимостью является 4, она записана в клетке (2,1). Сравниваем остаток у 2-го поставщика и потребности 1-го потребителя: , поэтому в клетку (2,1) записываем 30, так как запасы 2-го поставщика израсходованы, то в остальных клетках 2-й строки ставим прочерк. В оставшейся таблице минимальная стоимость 5 в клетке (3,1). Сравниваем запасы 3-го поставщика с потребностями 1-го потребителя: , поэтому в клетку (3,1) записываем 70, потребности 1-го потребителя удовлетворены, остаток запасов 3-го поставщика  записываем в клетку (3,4).

Получаем табл. 1.8.

Таблица 1.8

		100	80	90	80
	80	¾	80	¾	¾
	120	30	¾	90	¾
	150	70	¾	¾	80

Двойственная задача и (1.50) составляются с помощью правил, изложенных в разделе 1.10. Однако здесь есть свои особенности. В двойственной задаче должно быть  переменных. Те переменные, которые соответствуют поставщикам, обозначаются как , , а переменные, соответствующие потребителям, – , . Согласно теоремам двойственности ограничения в двойственной задаче принимают вид

, , ,                     (1.50)

а целевая функция

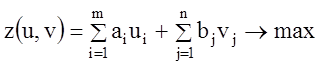.                   (1.51)

Соответственно в алгоритме решения транспортной задачи ищется решение двойственной задачи, а затем с помощью теории двойственности находится решение и исходной задачи. Этот алгоритм называется методом потенциалов, а решения , , и , , – потенциалами.

Используя сформулированные выше теоремы двойственности, можно вывести критерии для определения оптимальности полученного допустимого плана транспортной задачи.

Пусть получен некоторый допустимый план исходной задачи. Выпишем ограничения двойственной задачи, соответствующие ненулевым значениям переменных этого плана. Если рассмотренный план исходной задачи является оптимальным, то эти ограничения (1.50) должны выполняться как равенства при соответствующем решении двойственной задачи (вторая теорема двойственности). Выберем из (1.50) эти ограничения и получим систему уравнений

, , ,                        (1.52)

где  и  – подмножества, определенные условиями , , .

Эта система уравнений имеет множество решений, и пусть  – одно из этих решений. Это решение подставим в ограничения двойственной задачи (1.50), не вошедшие в систему уравнений (1.52). Если эти ограничения являются верными неравенствами при найденном решении, то проверяемый допустимый план исходной задачи является оптимальным. В противном случае – нет.

Пример 1.9. Проверить на оптимальность план примера 1.8.

Решение. Составим двойственную задачу.

, , ,

, , ,

, , ,

, , ,

.

Потенциалы (переменные двойственной задачи) определяются уравнениями

,        ,   ,

,        ,    .

Найдем решение этой системы, для этого одной из переменных (например, ) придадим произвольное числовое значение (удобнее всего положить  равным 0).

Рационально организовать процесс решения задачи в виде двойственной табл. 1.9.

Таблица 1.9

	2 80	1 0	3 4	4 -1	0
	4 20	3 80	1 20	7 0	2
	5 -7	8 -3	9 70	15 80	10
	2	1	-1	5

клетки которой заполнены частями ограничений двойственной задачи (клетки с ограничениями заштрихованы). Теперь, положив , последовательно находим потенциалы:

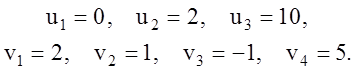                        (1.53)

Подставим найденные значения переменных двойственной задачи в остальные неравенства системы (1.50). Выпишем эти неравенства

,

,

,

,

,

.

Из вычислений видно, что неравенства второе, пятое и шестое являются неверными. Т.е. найденное решение (1.52) удовлетворяет не всем неравенствам ограничений. Следовательно, план не является оптимальным.

Следующий этап алгоритма – составление нового допустимого плана. Очевидно, что при составлении нового плана придется использовать незанятые клетки. Таких клеток будет не менее чем . Какую из них следует занять? Заполняя одну из незанятых клеток, приходится одновременно изменять числа по меньшей мере в трех уже заполненных клетках, чтобы не нарушить итоговое значение в строках и столбцах таблицы. Здесь следует использовать цикл, который должен строиться с учетом формул (1.50). Для транспортной задачи эти соотношения принимают вид:

, , .

Рассматривая только неверные неравенства, находим те из них, для которых правая часть наименьшая. Пусть это будет . . Следовательно, переменную  следует ввести в базис [занять клетку ].

Рассмотрим некоторый контур, включающий клетку . Пусть это будет цикл , ,  и . Клетка  свободна. Если переменную  включить в план: придать ей какое-нибудь значение, равное a, то число в клетке  следует уменьшить на эту величину, число в клетке  увеличить и, наконец, число в клетке  вновь уменьшить. Если , то такое изменение плана изменит целевую функцию на величину, равную

.

Очевидно, достаточно рассматривать те циклы, для которых  не положительна. Если обозначить клетки, в которых следует увеличить значения переменных, знаком “+”, то величина  равна наименьшему из чисел, размещенных в клетках со знаком “+”.