Следовательно, для более быстрого приближения к
оптимальному решению необходимо ввести в базис опорного решения переменную ![]() . Так как минимальное значение
. Так как минимальное значение ![]() достигается при
достигается при ![]() , то исключаем из базиса переменную
, то исключаем из базиса переменную ![]() . После первой итерации
симплекс-таблица примет вид:
. После первой итерации
симплекс-таблица примет вид:
|
№ |
|
|
1 |
4 |
1 |
0 |
0 |
|
|
|
|
|
|
|||
|
5 |
7 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1/5 |
1 |
1 |
-3/5 |
0 |
-2/5 |
0 |
|
3 |
21/5 |
1 |
0 |
7/5 |
1 |
3/5 |
0 |
|
|
22/5 |
1 |
4/5 |
1 |
1/5 |
0 |
|
|
|
0 |
-16/5 |
0 |
1/5 |
0 |
Так
как в строке ![]() есть отрицательная оценка
есть отрицательная оценка  , то решение
, то решение ![]() не
является оптимальным. Значит, с помощью симплекс-метода нужно улучшить решение,
найти другое решение, при котором значение функции
не
является оптимальным. Значит, с помощью симплекс-метода нужно улучшить решение,
найти другое решение, при котором значение функции ![]() будет
больше найденного
будет
больше найденного 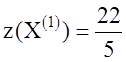 . При следующей итерации из
базиса выводится переменная
. При следующей итерации из
базиса выводится переменная ![]() , так как
, так как ![]() , а в базис вводится переменная
, а в базис вводится переменная ![]() , так как в столбце с отрицательной
оценкой есть только один положительный элемент 7/5, который находится в третьей
строке. После этой итерации симплекс-таблица примет вид:
, так как в столбце с отрицательной
оценкой есть только один положительный элемент 7/5, который находится в третьей
строке. После этой итерации симплекс-таблица примет вид:
|
№ |
|
|
1 |
4 |
1 |
0 |
0 |
|
|
|
|
|
|
|||
|
5 |
7 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
2 |
1 |
1 |
0 |
3/7 |
-1/7 |
0 |
|
2 |
3 |
4 |
0 |
1 |
5/7 |
3/7 |
0 |
|
|
14 |
1 |
4 |
23/7 |
11/7 |
0 |
|
|
|
0 |
0 |
16/7 |
11/7 |
0 |
Так как в строке ![]() нет
отрицательных оценок, то решение
нет
отрицательных оценок, то решение ![]() является
оптимальным. Но в исходной задаче не было переменных
является
оптимальным. Но в исходной задаче не было переменных ![]() и
и
![]() , поэтому в ответе их не учитываем и
получаем Хопт=(2, 3, 0),
, поэтому в ответе их не учитываем и
получаем Хопт=(2, 3, 0), ![]() .
.
Ответ: ![]() , Хопт=(2, 3, 0).
, Хопт=(2, 3, 0).
Задача 3. Для данной задачи линейного программирования построить двойственную, решить ее графически, по теореме двойственности найти решение исходной задачи:
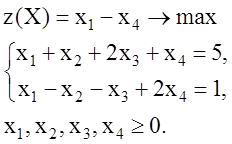
Решение. В исходной задаче:
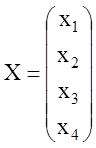 ,
, ![]() ,
, 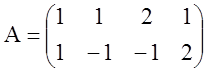 ,
,
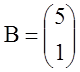 ,
,
то
есть нужно максимизировать функцию ![]() , если
, если ![]() и
и ![]() .
Тогда для этой задачи можно построить двойственную: минимизировать функцию
.
Тогда для этой задачи можно построить двойственную: минимизировать функцию ![]() , если
, если ![]() ,
где
,
где ![]() ,
, ![]() ,
, ![]() ,
,  ,
или
,
или
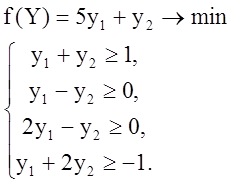 (2.2)
(2.2)
Решим
двойственную задачу графически. Для этого на плоскости ![]() построим
область допустимых планов. Заменяя знаки неравенств знаками равенств, получаем
уравнения четырех прямых:
построим
область допустимых планов. Заменяя знаки неравенств знаками равенств, получаем
уравнения четырех прямых:
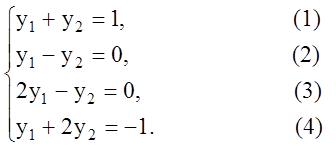
Построим эти прямые и пересечение соответствующих четырех полуплоскостей, которые образуют незамкнутую многоугольную область рис.2.2:
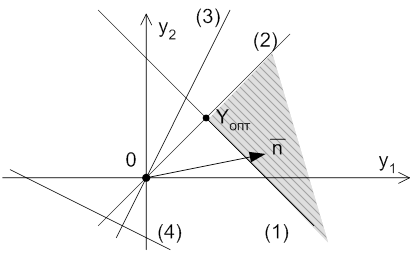
Рис.2.2
Строим
линию уровня ![]() , перпендикулярную к вектору
, перпендикулярную к вектору ![]() , и находим точку
, и находим точку 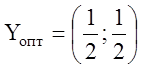 как решение системы уравнений
граничных прямых (1) и (2). Тогда решением двойственной задачи будет
как решение системы уравнений
граничных прямых (1) и (2). Тогда решением двойственной задачи будет 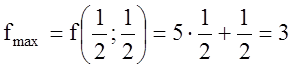 .
.
Подставим значения координат ![]() –
–
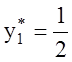 и
и 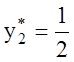 в
систему ограничений (2.2):
в
систему ограничений (2.2):
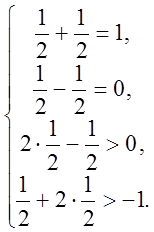
Так
как при подстановке оптимального решения ![]() в
систему ограничений (2.2) третье и четвертое ограничения выполняются как
строгие неравенства, то соответствующие координаты оптимального решения
исходной задачи равны 0, то есть
в
систему ограничений (2.2) третье и четвертое ограничения выполняются как
строгие неравенства, то соответствующие координаты оптимального решения
исходной задачи равны 0, то есть ![]() (см. п.1.10,
вторая теорема двойственности). Подставим эти значения в исходную систему
ограничений:
(см. п.1.10,
вторая теорема двойственности). Подставим эти значения в исходную систему
ограничений:
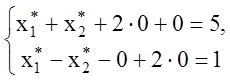 или
или 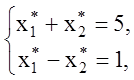
откуда ![]() ,
, ![]() . Значит,
. Значит, ![]() и
и
![]() .
.
Ответ: ![]() .
.
Задача 4. Решить транспортную задачу методом потенциалов:
|
45 |
15 |
20 |
20 |
|
|
25 |
9 |
5 |
3 |
10 |
|
55 |
6 |
3 |
8 |
2 |
|
20 |
3 |
8 |
4 |
8 |
Решение. Определим исходное опорное решение для данной транспортной задачи по методу «минимального элемента».
Просматривая элементы матрицы затрат, находим наименьший
элемент ![]() . Поэтому принимаем
. Поэтому принимаем ![]() и исключаем из дальнейшего рассмотрения
четвертый столбец, так как
и исключаем из дальнейшего рассмотрения
четвертый столбец, так как ![]() . Далее снова
находим в оставшейся матрице наименьший элемент
. Далее снова
находим в оставшейся матрице наименьший элемент ![]() (так
как
(так
как ![]() , то можно взять любой). Следовательно,
, то можно взять любой). Следовательно,
![]() . Теперь исключаем из дальнейшего
рассмотрения второй столбец. В матрице затрат снова находим минимальный элемент
. Теперь исключаем из дальнейшего
рассмотрения второй столбец. В матрице затрат снова находим минимальный элемент
![]() . Поэтому принимаем
. Поэтому принимаем ![]() и исключаем третью строку. Новый минимальный
элемент
и исключаем третью строку. Новый минимальный
элемент ![]() , следовательно,
, следовательно, ![]() . На этом шаге исключаем из рассмотрения
третий столбец. После этого остались невычеркнутыми клетки с номерами (1,1) и
(2,1). Минимальным оказывается
. На этом шаге исключаем из рассмотрения
третий столбец. После этого остались невычеркнутыми клетки с номерами (1,1) и
(2,1). Минимальным оказывается ![]() , откуда
, откуда ![]() . Наконец, на последнем шаге заносим
в единственную невычеркнутую клетку
. Наконец, на последнем шаге заносим
в единственную невычеркнутую клетку ![]() . Итак, получили
исходное опорное решение:
. Итак, получили
исходное опорное решение:
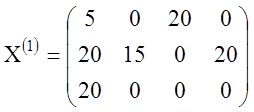 .
.
Ему
соответствует значение целевой функции ![]() .
.
Проверим, является ли найденное решение ![]() оптимальным? Для этого построим
систему потенциалов для найденного решения.
оптимальным? Для этого построим
систему потенциалов для найденного решения.
Согласно определению,
числа ![]() и
и ![]() (потенциалы)
должны удовлетворять
(потенциалы)
должны удовлетворять ![]() равенствам (в данном случае
равенствам (в данном случае
![]() ):
):
![]() ,
,
где
![]() - коэффициенты затрат,
соответствующие занятым клеткам для решения
- коэффициенты затрат,
соответствующие занятым клеткам для решения ![]() ,
то есть базисным переменным
,
то есть базисным переменным ![]() в опорном решении
в опорном решении
![]() . В данном примере получим следующие
шесть уравнений для определения неизвестных
. В данном примере получим следующие
шесть уравнений для определения неизвестных ![]() и
и
![]() :
:

Поскольку число уравнений на единицу меньше числа неизвестных,
одно неизвестное всегда оказывается свободным и ему можно придать любое
числовое значение. Положим ![]() . Тогда из первого
уравнения получаем
. Тогда из первого
уравнения получаем ![]() и из второго -
и из второго - ![]() . Из третьего уравнения, подставляя
. Из третьего уравнения, подставляя ![]() , находим
, находим ![]() и
из шестого уравнения
и
из шестого уравнения ![]() . Далее, из четвертого и
пятого уравнений после подстановки
. Далее, из четвертого и
пятого уравнений после подстановки ![]() получим
получим ![]() и
и ![]() .
Найденные значения потенциалов указаны в первом столбце и первой строке
таблицы:
.
Найденные значения потенциалов указаны в первом столбце и первой строке
таблицы:
|
|
|
|
|
||||||
|
45 |
15 |
20 |
20 |
||||||
|
|
25 |
9 |
5 |
3 |
10 |
||||
|
5 |
20 |
||||||||
|
|
55 |
6 |
3 |
8 |
2 |
||||
|
20 |
15 |
20 |
|||||||
|
|
20 |
3 |
8 |
4 |
8 |
||||
|
20 |
|||||||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.