Линейное программирование: Рабочая программа, контрольные работы и учебное пособие, страница 7

Переходим к построению следующей симплекс-таблицы (табл. 1.4). Для этого в соответствии с п.7 алгоритма из раздела 1.9

-  делим элементы второй (разрешающей) строки симплекс-таблицы 1.2 на разрешающий элемент ;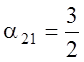

-  измененную вторую строку умножаем на , вычитаем её из первой строки и прибавляем к третьей строке.

Таблица 1.4

				5	2	-1	0	0
N
4		1	0	0			1	0
1		2	5	1			0	0
5		9	0	0			0	1
			10	5			0	0
				0			0	0

Получен новый опорный план . Он является оптимальным, поскольку в соответствии с теоремой 1.7 все , . Переменные ,  вспомогательные, поэтому .

1.10.Теория двойственности

Для любой задачи линейного программирования, называемой исходной, можно составить другую, которая называется двойственной.

В теории двойственности используются четыре пары двойственных задач. Приведём их.

1-2.  Задачи в стандартной (симметричной ) форме:

Исходная задача:

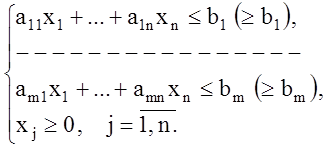                (1.45)

Двойственная задача:

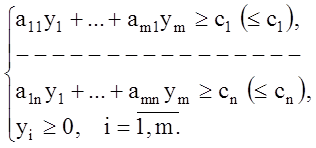                  (1.46)

3-4. Задачи в канонической форме

Исходная задача:

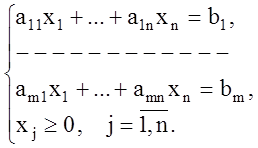
Двойственная задача:

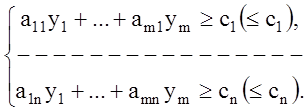
Правила составления двойственных задач

1.  Во всех ограничениях в неравенствах или в уравнениях исходной задачи свободные члены должны находиться в правой части, а члены с переменными – в левой.

2.  Если исходная задача на минимум, то знаки неравенств в системе ограничений « £ », если задача на максимум, то – « ³ ».

3.  Число переменных двойственной задачи равно числу условий в системе ограничений исходной задачи: при этом переменная, соответствующая ограничению-неравенству, должна быть неотрицательной, а переменная, соответствующая ограничению-равенству, может быть любой по знаку.

4.  Коэффициенты целевой функции двойственной задачи – это свободные члены в системе ограничений исходной задачи.

5.  Если исходная задача на максимум, то двойственная задача на минимум, и наоборот.

6.  Свободные члены системы ограничений двойственной задачи – это коэффициенты целевой функции исходной задачи.

7.  Матрица системы ограничений двойственной задачи – это транспонированная матрица системы ограничений исходной задачи.

Пример 1.6. Составить задачу, двойственную к данной:

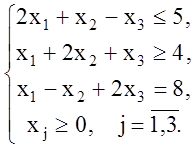
Решение. Так как задача на минимум, то все неравенства должны быть « ³ », поэтому умножим первое неравенство на , получим:

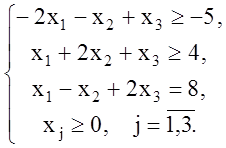
Теперь составляем двойственную задачу: ограничений в исходной задаче три. В двойственной задаче три переменные, причем первые два ограничения исходной задачи – неравенства, а третье – равенство, поэтому первые две переменные двойственной задачи должны быть неотрицательными, а третья может быть любой по знаку. Матрица системы ограниченной исходной задачи

,

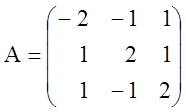тогда матрица ограничений двойственной задачи

.

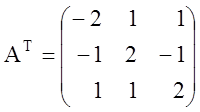Записываем двойственную задачу:

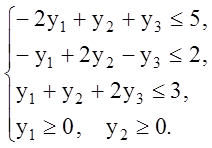
Связь между прямой и двойственной задачами не ограничивается взаимосвязью их форм записи. Она значительно глубже. Часть общих свойств прямой и двойственной задач содержится в приводимых ниже теоремах.

Первая теорема двойственности

Если одна из пары двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем значения целевых функций задач на своих оптимальных решениях равны.

Если одна из пары двойственных задач не имеет решения в силу неограниченности целевой функции, то другая не имеет решения в силу несовместности системы ограничений.

Вторая теорема двойственности

Если при подстановке оптимального решения в систему ограничений i-е ограничение исходной задачи выполняется как строгое неравенство, то i-я координата оптимального решения двойственной задачи равна нулю, и наоборот, если i-я координата оптимального решения двойственной задачи положительна, то I-е ограничение исходной задачи удовлетворяется оптимальным решением как равенство.

Пример 1.7. Для данной задачи составить двойственную и решить её графически, а затем, используя вторую теорему двойственности, найти решение исходной задачи:

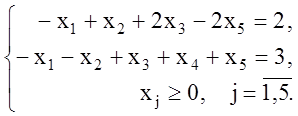
Решение. Составим двойственную задачу:

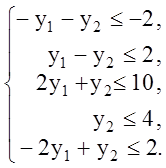
Решим её графическим способом. На рис. 1.7 изображен многоугольник ABCDE допустимых решений задачи.

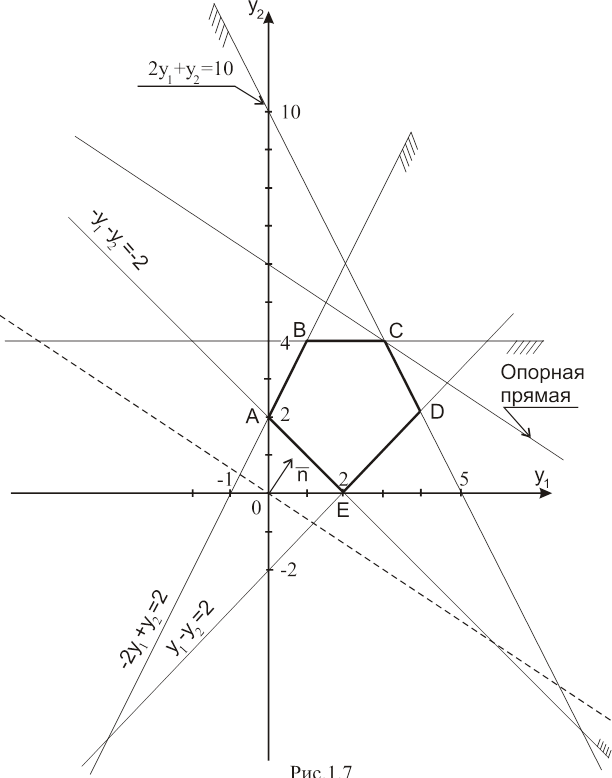
Решением является точка С – точка пересечения прямых  и .

Найдём её координаты:

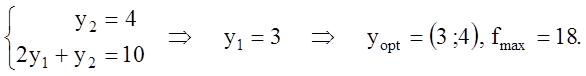
Подставим оптимальный план в систему ограничений:

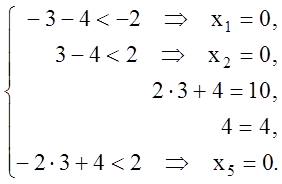
По второй теореме двойственности первая, вторая и пятая координаты оптимального плана исходной задачи равны нулю. Учитывая это, из системы ограничений исходной задачи получаем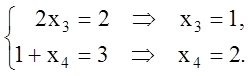            

Отсюда .

Ответ: ; .

5.11. Транспортная задача

Однородный груз сосредоточен у  поставщиков в объёмах . Груз нужно доставить  потребителям в объёмах . Известна - стоимость перевозки единицы груза от -го  поставщика -му потребителю. Требуется составить план перевозок, при котором все запасы будут полностью вывезены, запросы всех потребителей полностью удовлетворены и суммарные затраты на перевозку минимальны.

Исходные данные транспортной задачи обычно записываются в табл. 1.5.                                  Таблица 1.5

				…
				…
				…
	…	…	…	…	…
				…

В транспортных задачах под поставщиками и потребителями понимаются различные промышленные и сельскохозяйственные предприятия, заводы, склады, магазины и т.д. Однородными считаются грузы, которые могут быть перевезены одним видом транспорта. Под стоимостью перевозок понимаются тарифы, расстояния, время, расход топлива и т.п.