Пример 1.10. В условиях предыдущего примера перейти к новому допустимому плану.
Решение. Наименьшее значение в ограничениях правой части двойственной задачи достигается в клетке (3,1) (табл.1.9). Строим цикл (3,1), (3,3), (2,3), (2,1). При этом
![]() .
.
Целевая функция уменьшится на 7 единиц, если ![]() увеличится на единицу. Новый план примет вид табл.
1.10.
увеличится на единицу. Новый план примет вид табл.
1.10.
Таблица 1.10
|
100 |
80 |
90 |
80 |
||
|
80 |
2 80 |
1 -7 |
3 -3 |
4 -8 |
0 |
|
120 |
4 7 |
3 80 |
1 20 |
7 0 |
-5 |
|
150 |
5 20 |
8 -3 |
9 50 |
15 80 |
3 |
|
2 |
8 |
6 |
12 |
Потенциалы равны
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Проверка на оптимальность приводит к неравенствам
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
которые показывают, что и этот план не оптимален.
Замечание.
Очевидно, из всех циклов следует использовать только те, которые приводят к
наискорейшему убыванию целевой функции. В данном случае таковым является цикл
(2,2), (2,4), (3,4), (3,2), поскольку он приводит к уменьшению значения целевой
функции на ![]() единиц.
единиц.
В конце каждого шага проверяется условие, что потенциалы (переменные двойственной задачи) являются решениями этой задачи.
Пусть на некотором шаге получен очередной план и найдены
потенциалы для этого плана. Положительность всех оценок ![]() означает,
что найденный план оптимален.
означает,
что найденный план оптимален.
Пример 1.11. Для транспортной задачи, решение которой дается в таблице, проверить условие оптимальности.
Таблица1.11
|
100 |
80 |
90 |
80 |
|
|
80 |
2 ¾ |
1 0 |
3 ¾ |
4 80 |
|
120 |
4 ¾ |
3 30 |
1 90 |
7 ¾ |
|
150 |
5 100 |
8 50 |
8 ¾ |
15 ¾ |
Решение. Найдем потенциалы двойственной задачи:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Проверим выполнение оставшихся ограничений двойственной задачи:
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Все неравенства верны, следовательно:
1) ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() –
–
решения исходной задачи. Целевая функция будет равна
![]()
![]() ;
;
2) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() –
решения двойственной задачи.
–
решения двойственной задачи.
2. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Задача 1. Решить графически задачу линейного программирования с двумя переменными:
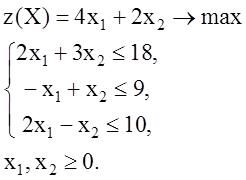
Решение. Построим область допустимых решений (планов) системы неравенств. Для этого, заменив неравенства в условии задачи на равенства, получим уравнения пяти прямых, образующих границу области допустимых решений:

Построим эти прямые и штриховкой
отметим полуплоскости, отвечающие каждому неравенству. Областью допустимых решений
(планов) в данном случае является выпуклый пятиугольник ![]() (см.
рис. 2.1). Далее, в той же системе координат строим вектор
(см.
рис. 2.1). Далее, в той же системе координат строим вектор ![]() , перпендикулярный к линиям уровня
, перпендикулярный к линиям уровня ![]() .
.
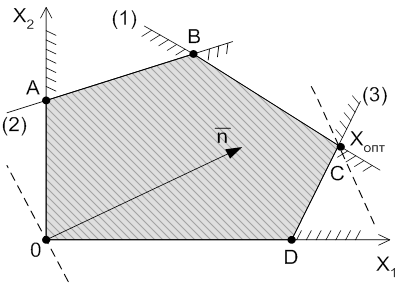
Рис. 2.1
Прямая, проходящая через начало координат перпендикулярно
к вектору ![]() , представляет собой линию уровня,
соответствующую значению
, представляет собой линию уровня,
соответствующую значению ![]() . Перемещение этой
прямой параллельно самой себе в направлении вектора
. Перемещение этой
прямой параллельно самой себе в направлении вектора ![]() приводит
к увеличению целевой функции
приводит
к увеличению целевой функции ![]() до тех пор, пока
она будет иметь общие точки с областью допустимых решений. Последней общей
точкой будет угловая точка С пятиугольника допустимых решений. Этому положению
линии уровня и соответствует
до тех пор, пока
она будет иметь общие точки с областью допустимых решений. Последней общей
точкой будет угловая точка С пятиугольника допустимых решений. Этому положению
линии уровня и соответствует ![]() . Для нахождения
координат точки
. Для нахождения
координат точки ![]() необходимо решить систему
уравнений граничных прямых (1) и (3):
необходимо решить систему
уравнений граничных прямых (1) и (3):
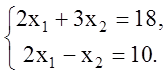
В результате получим искомое решение ![]() . Подставив значения
. Подставив значения ![]() и
и ![]() в
функцию
в
функцию ![]() , найдём
, найдём ![]() .
.
Ответ: ![]() .
.
Задача 2. Решить задачу линейного программирования симплекс-методом:
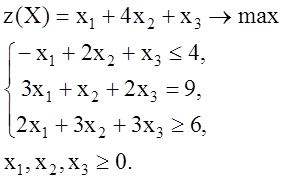
Решение. Так как система ограничений задана смешанно (есть как
уравнения, так и неравенства), то приведем ее к системе уравнений. Для этого
введем новые неотрицательные переменные ![]() и
и
![]() , тогда получим следующую систему
уравнений:
, тогда получим следующую систему
уравнений:
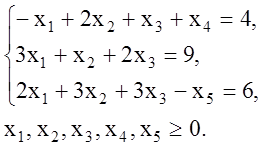 (2.1)
(2.1)
Применяя элементарные преобразования строк для расширенной матрицы этой системы, приведем систему уравнений (2.1) к единичному базису, то есть построим начальный опорный план. Преобразования нужно проводить таким образом, чтобы элементы последнего столбца (то есть свободные члены системы (2.1)) были бы неотрицательны. В данном случае процесс преобразования следующий:
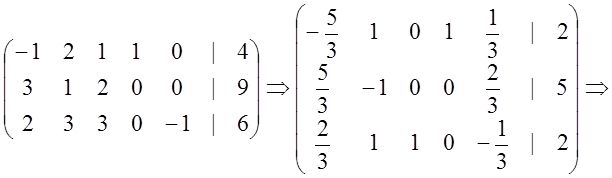
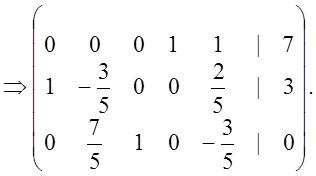
Таким образом, система (2.1) преобразуется к виду:
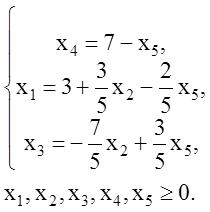
Переменные
![]() и
и ![]() будут
свободными, а
будут
свободными, а ![]() ,
, ![]() и
и
![]() - базисными. Полагая
- базисными. Полагая ![]() , получаем начальный опорный план:
, получаем начальный опорный план: ![]() .
.
Эти данные заносим в симплекс-таблицу.
|
№ |
|
|
1 |
4 |
1 |
0 |
0 |
|
|
|
|
|
|
|||
|
4 |
7 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
3 |
1 |
1 |
-3/5 |
0 |
0 |
2/5 |
|
3 |
0 |
1 |
0 |
7/5 |
1 |
0 |
-3/5 |
|
|
3 |
1 |
4/5 |
1 |
0 |
-1/5 |
|
|
|
0 |
-16/5 |
0 |
0 |
-1/5 |
Так как в строке ![]() есть
отрицательные оценки
есть
отрицательные оценки 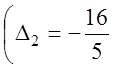 и
и 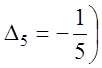 ,
то решение
,
то решение ![]() не является оптимальным [в силу того,
что функция
не является оптимальным [в силу того,
что функция ![]() в данном случае максимизируется].
Поэтому с помощью симплекс-метода нужно улучшить решение, то есть найти другое
решение, при котором значение функции
в данном случае максимизируется].
Поэтому с помощью симплекс-метода нужно улучшить решение, то есть найти другое
решение, при котором значение функции ![]() будет
больше найденного
будет
больше найденного ![]() .
.
Определим, введение какой из переменных – ![]() или
или
![]() – приведет к большему приращению
целевой функции, которое находится по формуле:
– приведет к большему приращению
целевой функции, которое находится по формуле:
![]() ,
,
где ![]() – номер переменной, вводимой в
базис,
– номер переменной, вводимой в
базис, ![]() – соответствующая оценка в строке
– соответствующая оценка в строке ![]() ,
, 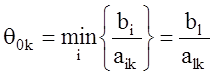 при
при
![]() ,
, ![]() –
свободные члены,
–
свободные члены, ![]() – коэффициенты основной
матрицы,
– коэффициенты основной
матрицы, ![]() – номер переменной, выводимой из
базиса.
– номер переменной, выводимой из
базиса.
Вычисляем значение параметра ![]() для переменных
для переменных ![]() и
и ![]() :
:
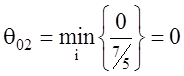 при
при
![]() ,
,
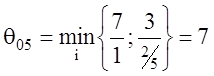 при
при ![]() .
.
Находим возможные приращения целевой функции при
введении в базис каждой из переменных ![]() или
или
![]() и определяем наибольшее из них:
и определяем наибольшее из них:
![]()
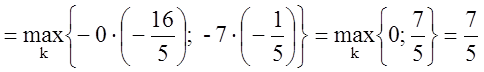 при
при ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.