Расчет и проектирование редуктора общего назначения, страница 6

4.3. Предварительный выбор подшипников

Подшипники для быстроходного вала закрытой конической передачи выбираем роликовые конические типа 7000 легкой серии, установленные врастяжку. Для тихоходного вала подшипники выбираем роликовые конические типа 7000 легкой серии, установленные враспор.

Параметры подшипников отразим в таблице:

Вал	Подшипник
Вал	Обознач.	d, мм	D, мм	T, мм	C_r, кН	e	Y
Б	7208	40	80	20	42,4	0,38	1,56
Т	7209	45	85	21	42,7	0,41	1,45

4.4. Определение нагрузок, действующих на валы редуктора

Редукторные валы испытывают деформации изгиба и кручения. Деформация кручения возникает при действии вращающих моментов, приложенных со стороны двигателя и рабочей машины. Деформация изгиба валов вызывается силами в зубчатом зацеплении закрытой передачи и консольными силами со стороны открытой передачи и муфт

Расчет проведем в табличной форме.

Источник силы	Обознач.	Формула	Единица измерения	Значение
1	2	3	4	5
Муфта	F_м	F_м = C_Δ_r ∙ Δr	Н	488

Закрытая передача
Колесо
Окружная	F_ЗПt2	!Ошибка в формуле	Н	2409
Радиальная	F_ЗПr2	F_ЗПr2 = F_ЗПa1	Н	1892
Осевая	F_ЗПa2	F_ЗП_a₂ = F_ЗП_r₁	Н	625
Шестерня
Окружная	F_ЗПt1	F_ЗП_t1 = F_ЗП_t2	Н	2409
Радиальная	F_ЗПr1	F_ЗПr1 = F_ЗП_t1 ∙ γ_r	Н	625
1	2	3	4	5
Коэффициент силы	γ_r		–	0,26
Осевая	F_ЗПa1	F_ЗП_a₁ = F_ЗП_t1 ∙ γ_a	Н	1892
Коэффициент силы	γ_a		–	0,79
Открытая передача
Колесо
Окружная	F_ОПt2	!Ошибка в формуле	Н	3408,154
Радиальная	F_ОПr2	F_ОПr2 = F_ОПt2 ∙ tg α	Н	1240,466
Шестерня
Окружная	F_ОПt1	F_ОПt1 = F_ОП_t2	Н	3408,154
Радиальная	F_ОПr1	F_ОПr1 = F_ОПr₂	Н	1240,466

Примечание: все индексы величин, входящих в формулы для расчета сил в зацеплении вводятся в соответствующих разделах

После того как определили внешние силовые факторы, определим реакции в опорах и построим эпюры внутренних силовых факторов. Для этого необходимо знать, кроме значений самих сил, значений их плеч относительно базовой точки. Для быстроходного вала такой точкой будет точка A, а для тихоходного вала – точка D.

Выпишем все плечи:

Быстроходный вал:

l_MA = 89 мм; l_AB = 59 мм; l_BO = 24 мм; l_OO_’ = 20,15 мм

Здесь: M–точкаприложения силы от муфты;
A и B – точки приложения реакций опор;

O’ – точка приложения сил зацепления;
O – проекция точки O’ на ось вала.

Тихоходный вал:

l_CO = 58 мм; l_OD = 43 мм; l_DS = 72 мм; l_OO_” = 83 мм; l_SS_’ = 54 мм

Здесь: S’ – точка приложения сил зацепления открытой передачи;
S – проекция точки S’ на ость вала
C и D – точки приложения реакций опор;
O” – точка приложения сил зацепления;
O – проекция точки O” на ость вала.

Определим реакции опор на быстроходном валу. Для этого составим уравнения статики: уравнения изгибающих моментов M_y и M_z относительно точки A и уравнение баланса сил.

Принято следующее правило знаков: момент, направленный против часовой стрелки относительно точки вращения вокруг выбранной оси – положителен. Сила, направление которой совпадает с направлением оси – положительна

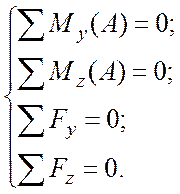
!Ошибка в формуле

Таким образом, радиальные реакции в опорах будут равны:

!Ошибка в формуле; !Ошибка в формуле.

!Ошибка в формуле;

!Ошибка в формуле.

Так как используются радиально-упорные подшипники, то определим осевые реакции в опорах. В таких опорах радиальная сила вызывает также дополнительную осевую реакцию и распределение их по опорам зависит от способа установки подшипников. В данном случае опоры установлены в распор, поэтому:

!Ошибка в формуле; !Ошибка в формуле.

!Ошибка в формуле;

!Ошибка в формуле.

Определим реакции опор на тихоходном валу. Для этого составим уравнения статики: уравнения изгибающих моментов M_y и M_x относительно точки D и уравнение баланса сил.

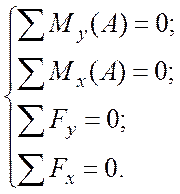
!Ошибка в формуле

Радиальные реакции в опорах будут равны:

!Ошибка в формуле; !Ошибка в формуле.

!Ошибка в формуле;

!Ошибка в формуле.

1 2 3 4 5 6 7 8 9 10 11

Скачать файл