Расчет и проектирование редуктора общего назначения, страница 2

N = 573 ∙ ω ∙ L_h,

для шестерни:

N₁ = 573 ∙ ω₁ ∙ L_h; N₁ = 573 ∙ 75,4 с^-1 ∙ 10 000 ч = 4,3∙10⁸;

для колеса;

N₂ = 573 ∙ ω₂ ∙ L_h; N₁ = 573 ∙ 18,8 с^-1 ∙ 10 000 ч = 1,1∙10⁸

Значения N_H01 и N_H02 определяем в зависимости от средней твердости поверхности шестерни и колеса линейной интерполяцией по известным значениям на границах интервалов, включающих реальные значения HB_1ср (HRC_1ср) и HB_2ср:

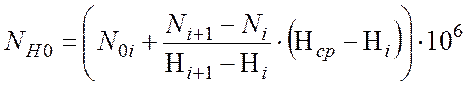
Здесь  и, соответственно, а N_i и N_i+1 – количество циклов, соответствующих средним твердостям H_i; H_i+1.

Для шестерни:

.

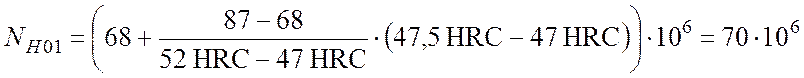Для колеса:

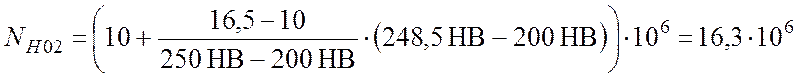
Так как N₁ > N_H01 и N₂ > N_H02, то коэффициенты долговечности для шестерни и колеса будут равны:

K_HL1 = 1; K_HL2 = 1.

Таким образом

[σ]_H1 = 1 ∙ 835 = 835 Н/мм²;

[σ]_H2 = 1 ∙ 514 = 514 Н/мм².

И значит, что расчетное допустимое контактное напряжение будет равно

[σ]_H = 0,45(835 + 514) = 607 Н/мм²,

но полученное значение превышает наименьшее допустимое контактное напряжение (колеса) более чем в 1,15 раза, поэтому принимаем:

[σ]_H = 1,15 ∙ [σ]_H2;

[σ]_H = 1,15 ∙ 514 = 591 Н/мм².

2.3. Определение допустимых напряжений изгиба

Допускаемые напряжения изгиба определяются аналогично допускаемым контактным напряжениям. Пересчет предельных свойств материала осуществляется по коэффициенту долговечности:

[σ]_F1 = K_FL1 ∙ [σ]_F01; [σ]_F2 = K_FL2 ∙ [σ]_F02,

где

.

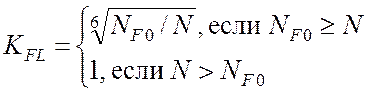Здесь N_F0 – число циклов перемены напряжений, соответствующее пределу выносливости; N – число циклов перемены напряжений за весь срок службы.

По статистике: N_F01 = N_F02 = 4∙10⁶; N₁ = 4,3∙10⁸, N₂ = 1,1∙10⁸ (см. предыдущий раздел). Так как N₁ > N_F01 и N₂ > N_F02, то коэффициенты долговечности для шестерни и колеса будут равны:

K_FL1 = 1; K_FL2 = 1.

Таким образом

[σ]_F1 = 1 ∙ 310 = 310 Н/мм²;

[σ]_F2 = 1 ∙ 296 = 296 Н/мм².

Расчет ведем по минимальному напряжению, следовательно:

[σ]_F = 296 Н/мм²

2.4.    Определение основных геометрических
параметров передачи

Главным проектным параметром конической зубчатой передачи является внешний делительный диаметр колеса d_e2. Оценочное значение можно определить по статистике, в зависимости от массы редуктора. Масса в первом приближении определится по формуле

m = γ ∙ T₂,

где γ = 0,1÷0,2 кг/(Н∙м) – удельный вес редуктора. Тогда, принимая
γ = 0,2 кг/(Н∙м), масса редуктора будет равна

m = 0,2 ∙ 196 Н∙м = 39 кг.

Поэтому ориентировочное значение внешнего делительного диаметра колеса

d_e2 ≈ 200 мм

Уточненное значение определяется по следующей формуле:

,

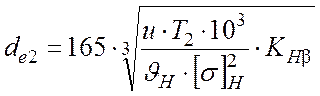где   K_Hβ = 1,1   –  коэффициент распределения нагрузки для колес с круговым зубом;

         = 1,5   –  коэффициент вида конической передачи для колес с круговым зубом при твердости шестерни ≥45HRC и колеса ≤350HB.

Таким образом

.

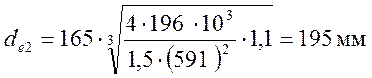Полученное значение необходимо округлить до ближайшего значения из нормального ряда линейных размеров. Поэтому принимаем

d_e2 = 190 мм

(меньшее значение выбираем для обеспечения более высокой экономичности).

Углы делительных конусов шестерни (δ₁) и колеса (δ₂) определяются следующими соотношениями:

δ₂ = arctg u; δ₁ = 90° – δ₂.

δ₂ = arctg 4 = 75°57’45”;

δ₁ = 90° – 75°57’45” = 14°2’15”.

Определим внешнее конусное расстояние R_e по формуле:

;

.

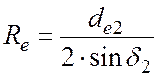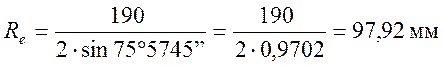Зная значение R_e, можно определить ширину зубчатого венца шестерни и колеса:

b = ψ_R ∙ R_e,

где   ψ_R = 0,285 –  коэффициент ширины венца.

b = 0,285 ∙ 97,92 = 27,91 мм.

Округляем полученное значение до целого по ряду R_a40: b = 26 мм

Внешний окружной модуль зацепления определяется по формуле:

,

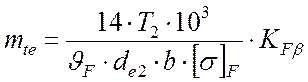где   K_Fβ = 1,08  –  коэффициент распределения нагрузки по ширине венца для прирабатывающихся колес с круговым зубом;

         = 1       –  коэффициент вида конических колес.

Таким образом

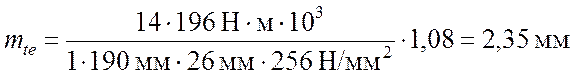
Определим число зубьев колеса и шестерни по формулам

!Ошибка в формуле; !Ошибка в формуле.

z₂ = 190 / 2,35 = 80,85 ≈ 81;

z₁ = 81 / 4 = 20,25 ≈ 20.

В связи с округлением изменилось передаточное отношение. Необходимо его уточнение при условии, что это изменении составляет менее 4% расчетного:

u_ф= z₂ / z₁; u_ф= 81 / 20 = 4,05;

!Ошибка в формуле;

!Ошибка в формуле

Так как мы определили фактическое передаточное отношение, то необходимо определить действительные углы делительных конусов колеса и шестерни:

δ₂ = arctg u_ф; δ₁ = 90° – δ₂.

δ₂ = arctg 4,05 = 76°7’48”;

δ₁ = 90° – 75°57’45” = 13°52’12”.

Для определения внешних диаметров колеса и шестерни необходимо назначить коэффициенты смещения режущего инструмента. Так как разность средних твердостей поверхности шестерни и колеса

H_1ср – H_2ср = 457– 248,5 = 208,5 HB

больше 100, то смещение инструмента не требуется, то есть

x_n1 = x_n2 = 0

Определим внешние диаметры шестерни и колеса.

Делительные диаметры:

d_e1 = m_te ∙ z₁; d_e2 = m_te ∙ z₂.

d_e1 = 2,35 ∙ 20 = 47,03 мм;

d_e2 = 2,35 ∙ 81 = 190,49 мм.

Диаметры вершин:

d_ae1 = d_e1 + 1,64∙(1 + x_n1)∙m_te ∙ cos δ₁;

d_ae2 = d_e2 + 1,64∙(1 – x_n1)∙m_te ∙ cos δ₂.

d_ae1 = 47,03 + 1,64∙(1 + 0)∙2,35 ∙ cos 13°52’12” = 50,78 мм;

d_ae2 = 190,49 + 1,64∙(1 – 0)∙2,35 ∙ cos 76°7’48” = 191,41 мм.

Диаметры впадин:

d_fe1 = d_e1 – 1,64∙(1,2 – x_n1)∙m_te ∙ cos δ₁;

d_fe2 = d_e2 – 1,64∙(1,2 + x_n1)∙m_te ∙ cos δ₂.

d_fe1 = 47,03– 1,64∙(1,2 – 0)∙2,35 ∙ cos 13°52’12” = 42,54 мм;

d_fe2 = 190,49– 1,64∙(1,2 + 0)∙2,35 ∙ cos 76°7’48” = 189,38 мм.

Средние делительные диаметры:

d₁ = 0,857∙d_e1; d₂ = 0,857∙ d_e2.

d₁ = 0,857 ∙ 47,03 = 40,31 мм;

d₂ = 0,857 ∙ 190,49 = 163,25 мм

2.5. Проверочный расчет

Для гарантии качественного изготовления шестерни и колеса необходимо, чтобы размеры заготовок колес не превышали предельных значений для выбранных материалов:

D_заг1 ≤ D_пред1; S_заг2 ≤ S_пред2.

Здесь     D_заг1   –  диаметр заготовки шестерни

D_заг1 = d_ae1 + 2∙m_te + 6 мм;

D_заг1 = 50,78 + 2 ∙ 2,35 + 6 = 62 мм < 125 мм;

              S_заг2    –  размер заготовки

S_заг2 = 8 ∙ m_te;

S_заг2 = 8 ∙ 2,35= 17 мм < 125 мм;