Елементи теорії функцій комплексної змінної. Інтегральне перетворення Лапласа. Дискретне перетворення Лапласа

ЕЛЕМЕНТИ ТЕОРІЇ ФУНКЦІЙ

КОМПЛЕКСНОЇ ЗМІННОЇ

1.1 Границя, неперервність, похідна функції комплексної змінної.

           Означення. Хай є деяка множина D точок комплексної площини Z. Точка z називається внутрішньою точкою множини D. При цьому під кругом з центром в нескінченно віддаленій точці z=∞ розуміють зовнішність довільного кола │z│=R з центром в тчці z=0.

Означення. Областю накомплексній площині називається множина точок D, всі точки якої внутрішні (відкритість області) і дві довільні точки якої з'єднуються ломаною лінією, що належить множині D (зв'язаність області).

Означення.Межовою точкою області D називається така точка, яка належить області D, але в довільному околі якої є точки, що не належить D.

Означення. Межою G області D називають множину межових точок області.

Означення. Замкненою областю називають область D=DUG.

           Приклад 1: Круг |z|<1 є область. Межею цієї області є коло |z|=1. Область |z|≤1 буде замкненою.

          Означення. Область D називається однозв'язаною, якщо довільну замкнену лінію із області можна стягти в точку, не входячи за межі області. В протлежному випадку область D називається багатозв'язаною.

         Означення. Область D називається обмеженою, якщо вона належить деякому колу |z|<R.

Приклад 2: Кільце r<|z|<R обмежена двозв'язана область.

          Означення. Кажуть, що на комплексній множині D задана функція ω=f(z), якщо кожній точці із D поставлено у відповідність одна (однозначна функція), або декілька точок ω (багатозначна функція).

Вважаючи z=x+iy, ω=u+iv,

одержемо u+iv=f(x+iy)=u(x,y)+iv(x,y),

звідси u=Ref(z), v=Imf(z)

        Означення. Функція f(z) має границю при z →  (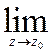f(z)), якщо існують границі функцій дійсних змінних

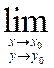u(x, y) = , limv(x, y)=,

при цьому

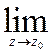f (z) = =.

           Означення. Функція f(z) називається неперервною в точці , якщо вона визначена в деякому колі точки , і 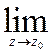f(z) = f().

          Означення. Функція називається неперервною в області D, якщо вона неперервна в кожній точці області D.

        Очевидно, що функція f(z) неперервна тоді і тільки тоді, коли неперервні функціі u і v.

          Для фуекціі, неперервних в замкнених областях, виконуються звичайні властивості функцій, неперервних на замкнених інтервалах.

          Означення. Похідною фуекціі f(z) будемо називати  границю:

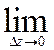
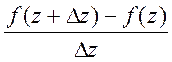
                           (z) =         (1)

якщо остання існує. При цьому границя не залежить від шляху, по якому точка z+ прямує до точки z.

          ТЕОРЕМА. (Умови Коші - Рімана ). Для того, щоб функція f(z) мала похідну в точці z=z+iy, необхідно і достатньо, щоб

1)  функціі u(x, y) i v(x, y), були диференційовані в точці (x, y)

2)  в цій точці виконувались рівності

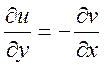= , .                      (2)

Доведення. Нехай функція диференційована в точці z. Візмемо . В цьому випадку

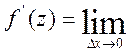
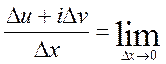
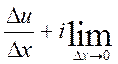
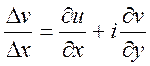. (3)                                                                                       (3)

          Якщо прийняти   то будемо мати

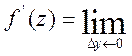
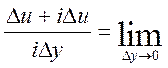
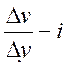
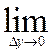
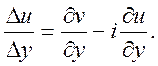(4)                                                                                             (4)

Вирази (3) і (4) повинні бути рівними, тому

, .

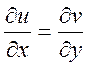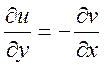          Доведено, що умови (2) достатні для диференційованості функціі f(z). Прирісти функцій u і v можна зобразити так:

,

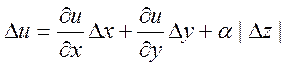                                                                  (5)

                                                   

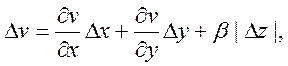
де  і  при  .

          Далі

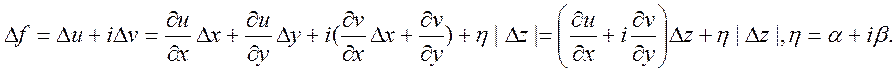
звідси

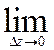
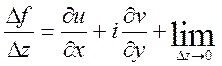
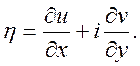
          Теорему доведено.

          Функція комплексної змінної зберігає всі відомі правила диференціювання:

1.

2.

3.            

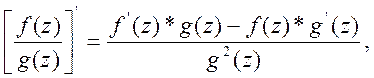
          4.

          5.

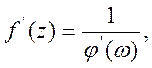
          де f і  - взаємно обернені фуекції.

          Приклад 3. розглянемо функцію  Для неї  

звідси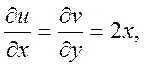  

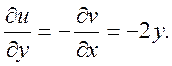
          умови Коші-Рімана виконуються для всіх точок z.

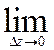
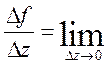
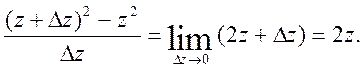
          Означення. Функція f(z) однозначна і диференційована в кожній точціобласті D називається аналітичною (регулярно або голоморфною) в ційобласті.

          Вправи. Знайти похідні функцій f(z):

1)  2) sin z, 3) cos z, 4) ln z.

        1.2 Інтеграл від функції комплексної змінної

          Хай в області D на комплексній площині (Z) задна однозначна і неперервна функція  і С – довільно кусково – гладка крива, що належить D. Розб'ємо криву С довільним чином на малі частки точками  і розглянемо суму

                                                    (6)

де  і  - довільна точка на ділянці (). Сума (6) називається інтегральною сумою функції.

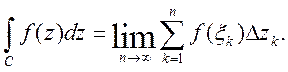          Означення. Границя інтегральних сум (6) обчислених для довільної послідовності розбиття С при умові, що max||  k=1, 2, …, n, називається інтегралом від функції f(z) вздовш кривої С і позначається символом

                (7)

          В прийнятих припущеннях інтеграл існує і не залежить від вибору розбиття С та від вибору точок  Якщо функція f(z) аналітична в однозв'язній області, то інтеграли по всім шляхям, що сполучують точки А і В, збігаються, а інтеграли по довільному замкненому контуру G дорівнюють нулю.

          Важливе значення в теорії функцій комлексної змінної відіграє формула Коші, що зв'язує значення аналітичної функції на самому контурі:

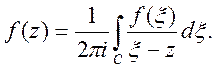                                                    (8)

          Доведемо цю формулу. Хай С – замкнений контур (рис. 1), який повністю належить однозв'язній області D, z – фіксована внутрішня точка області, що обмежена контуром С.

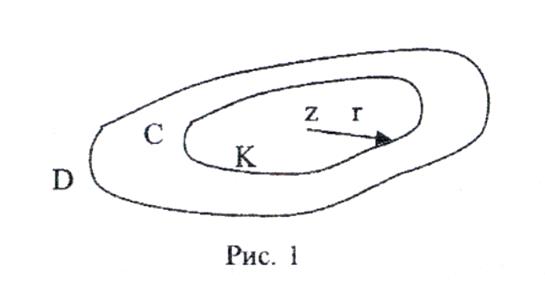
        Підінтегральна функція в інтегралі (8) аналітична в області D, за виключенням точки z. Виключемо цю точку кругом радіуса r з центром в точці z.

          В кільці, обмеженом контурами С і К (рис. 1), підінтегральна функція аналітична, тому

.

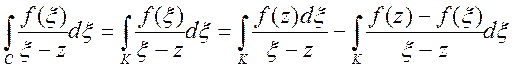           На контурі К ,  тому

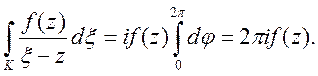
          Для другого інтеграла будемо мати

≤

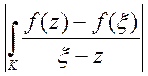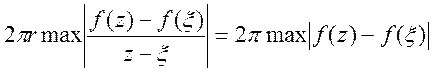
          Так як, f(z) – неперервна, то  при

          Звідси

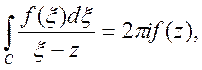
 або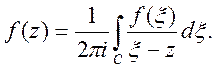                  

 таким чином доведено правильність формули Коші (8).

          Використовуючи формулу Коші, можна отримати вираз для n-ої похідної функції f(z):

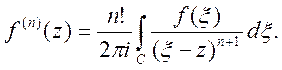
                      (9)
          Вправи. 1. обчислити інтеграл 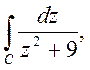 якщо точка 3і лежить в середині контура С, а точка – 3 – зовні.

          2. Обчислити інтеграл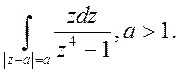

          3. обчислити інтеграл 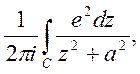 якщо контур С містить в середині себе круг

       1.3 Ряди Тейлора

В теорії функцій комплексної змінної всі основні поняття теорії рядів з дійсними членами зберігаються.

          Так, наприклад, має місце теорема Абеля:

          ТЕОРЕМА 1. Якщо степеневий ряд

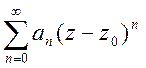                                                        (10)

де  - задані комплексні числа, збігається в крайнім разі у одній точці  то існує круг радіуса R з центром у точці  такий, що ряд (10) збігається у крузі  і розбігається в зовнішності круга