Теория поля: Методические указания к выполнению семестрового задания (с вариантами заданий)

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ

МЕТОДИЧЕСКИЕ  УКАЗАНИЯ

для студентов металлургических специальностей

к выполнению семестрового задания по теме «Теория поля»

с вариантами заданий

Рекомендовано  на заседании кафедры высшей математики

Протокол № 4 от 14.02.2002 г.

Утверждено на заседании

методсовета ДГМИ

Протокол № 8 от 22.04.2002 г.

Алчевск, 2002

1 Скалярное поле

Функция U=U(p)=U(x,y,z) называется скалярной, если она характеризуется только числовым значением. Если в каждой точке некоторой области задана скалярная функция U, то говорят, что в этой области задано скалярное поле. Примером скалярного поля может служить поле температур неравномерно нагретого тела, поле плотностей распределения электрических зарядов в изолированном наэлектризованном теле, поле потенциалов электрического поля и т.д.

Скалярное поле может совпадать со всем пространством, если функция U определена в любой точке, или являться некоторой его частью, если функция U определена только в этой части пространства.

Скалярное поле называется стационарным, если функция U=U(p) не зависит от времени t, и называется нестационарным, если такая зависимость функции U от t существует.

Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция U принимает постоянное значение, т.е.

U (x,y,z) = C.

В курсе физики при рассмотрении поля потенциала поверхности уровня называют обычно эквипотенциальными поверхностями (т.е. поверхностями равного потенциала).

Если скалярное поле плоское, т.е. U = U(x,y), то поверхности уровня будут линиями уровня

U (x,y) = C.

Уравнение поверхности уровня, проходящей через данную точку M₀ (x₀,y₀,z₀) записывается так:

U (x,y,z) = U (x₀,y₀,z₀).

Примеры.

1) Найти линии уровня скалярного поля U = xy

Решение.

Линии уровня удовлетворяют уравнению:

xy = C или ,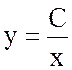

т.е. линиями уровня будет семейство гипербол в 1-й и 3-ей четвертях при C>0 или во 2-й и 4-й четверти при C<0.

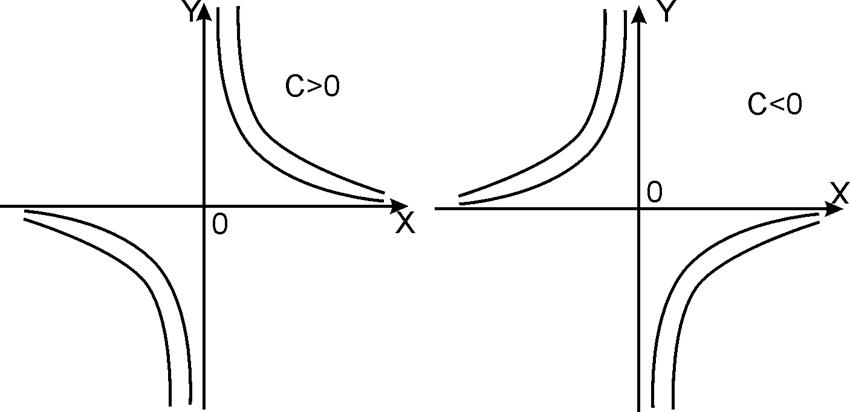
Рисунок 1                                  Рисунок 2

2) Найти поверхность уровня скалярного поля U=2x+y+3z, проходящего через точку (1,1,1)

Решение.

Найдем U(1,1,1)=2+1+3=6, тогда поверхность уровня, проходящая через точку (1,1,1) будет иметь уравнение

2x+y+3z=6.

Это уравнение плоскости, отсекающей на осях OX, OY, OZ соответственно отрезки 3, 6, 2.

На рисунке 3 показана только часть плоскости при , ,

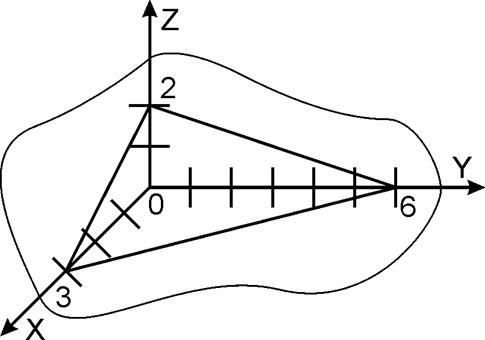
            Рисунок 3

2 Производная по направлению

Важной характеристикой скалярного поля является скорость изменения поля в заданном направлении.

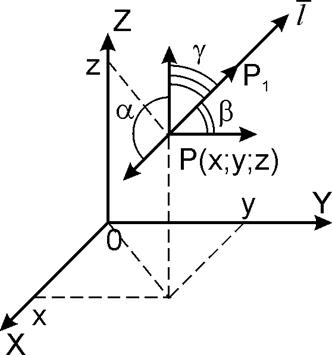
Пусть задано скалярное поле U=U(x,y,z). Возьмем в поле точку P(x,y,z) и луч , из нее выходящий. Вектор  образует с осями ОХ, ОY, OZ соответственно углы , , . Если =(l_х, l_у, l_z), то направляющие косинусы вектора  будут такими:

,  ,  .

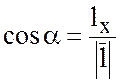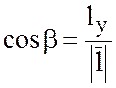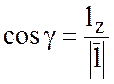Тогда единичный вектор

.

Рисунок 4

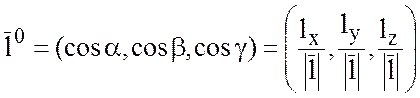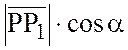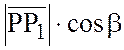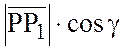Возьмем точку Р₁(x₁,y₁,z₁), лежащую на луче . Проекции вектора  на оси координат будут , , , если обозначить 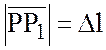, то . А с другой стороны =(х₁-х, y₁-y, z₁-z). Тогда:

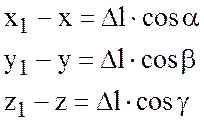  или  

Тогда приращение функции U при переходе из точки Р в точку Р₁ будет:

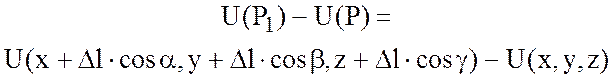                               (1)

Когда точка Р₁ будет менять свое положение на луче , то в формуле (1) будет меняться только .

Доказательство.

Так как полное приращение функции

,

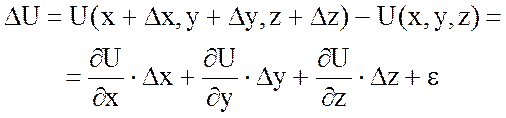где  - бесконечно малая величина более высокого порядка, малости, чем 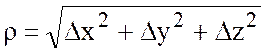. Так как , , , то

.

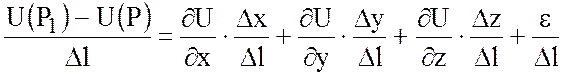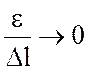, когда 0, т.к.  более высокого порядка малости, чем .

Тогда

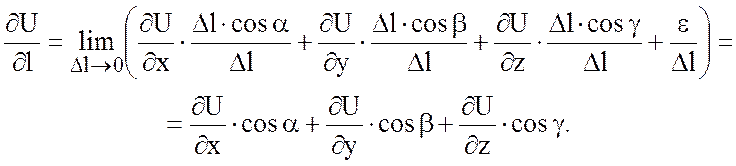
Пример.

Найти производную функции  в т. А(1;-1;2) по направлению , если В(-1;2;3).

Решение.

Найдем координаты вектора .

=(-2;3;1), тогда, так как 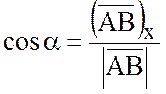 , , , 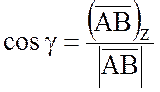то

,

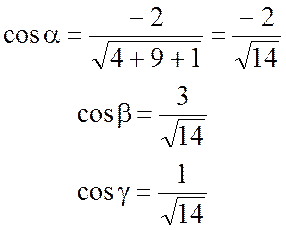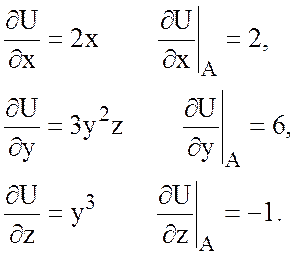
Тогда

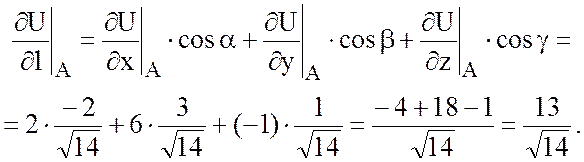
3 Градиент векторного поля

Градиентом векторного поля называется вектор, проекциями которого служат значения частных производных этой функции, т.е.

.

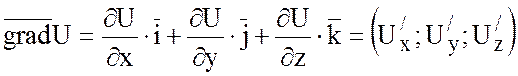Обозначают градиент вектора так:  или

Производная функции по данному направлению , , 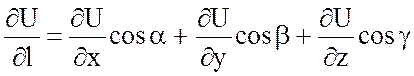или равна скалярному произведению градиента функции на единичный вектор этого направления .

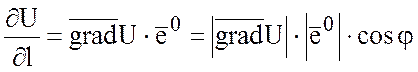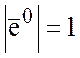Т.к. , где и  - угол между  и . Тогда производная по направлению достигает наибольшего значения, когда =1, т.е. при =0. Это наибольшее значение равно 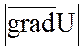. Т.е.  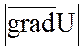есть наибольшее возможное значение производной  в данной точке Р, а направление  совпадает с направлением луча, выходящего из точки Р, вдоль которого направление наискорейшего возрастания функции. В направлении противоположном направлению градиента функция U будет быстрее всего убывать. Направление градиента функции U(x,y,z) в каждой точке совпадает с направлением нормали к поверхности уровня скалярного поля, проходящей через эту точку, т.к. уравнение нормали к поверхности уровня в точке :

.

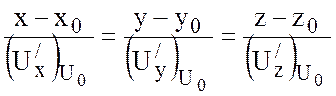Итак, градиент обладает такими свойствами:

1) Градиент направлен по нормали к поверхности уровня (или к линии уровня, если поле плоское).

2) Градиент направлен в сторону возрастания функции поля.

3) Модуль градиента равен наибольшей производной по направлению в данной точке поля:

.

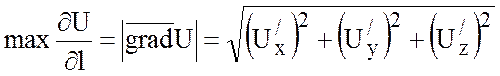Для облегчения нахождения градиента пользуются такими его свойствами:

1) .

2) .

3) .

4) .

Примеры.

1) Найти градиент скалярного поля .

Решение.

.

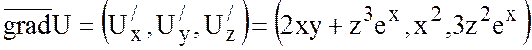2) Найти косинус угла между градиентами функции U в точках (1;-1;0) и (0;1;-1), если .

Решение.

,

,

,

.

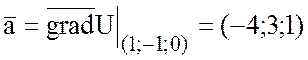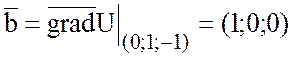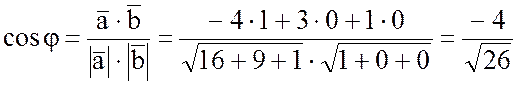3) Найти наибольшую скорость изменения функции поля  в точке (1;1;1)

Решение.

,

,

.

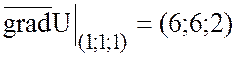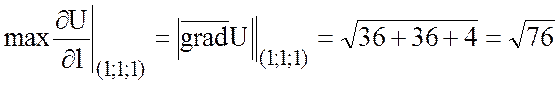4 Векторное поле

Если в каждой точке Р области Д задан определенный вектор, то говорят, что в этой области задано векторное поле.

Примерами векторных полей могут служить силовые поля, поля скоростей текущей жидкости и др. Различают стационарные векторные поля, когда вектор , задающий поле, зависит только от координат точки Р и не зависит от времени, и нестационарные, когда такая зависимость от времени существует.

Если поле стационарно и координаты точки P (x;y;z), то .

Векторное поле называется однородным, если  - однородный вектор, т.е. , ,  - постоянные величины. Примером однородного поля может служить поле тяжести.

Векторное поле будет плоским, если , т.е. если =0. С плоскими полями часто встречаются в гидродинамике при изучении плоских течений жидкости.

5 Векторные линии векторного поля

Векторной линией векторного поля называется линия, в каждой точке которой направление касательной совпадает с направлением вектора, задающего поле в этой точке.

Для магнитного поля векторными (силовыми) линиями будут линии, выходящие из северного полюса и оканчивающиеся в южном. Расположение силовых линий важно в физике при изучении электрических, магнитных и электромагнитных полей.

Дифференциальные уравнения векторных линий имеют вид :

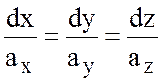                      .                                          (2)

Они получены из условия параллельности вектора  и вектора, направленного по касательной к векторной линии, который имеет координаты, пропорциональные производным , , , или, что то же самое, дифференциалам , , .

Система (2) уравнений представляет систему дифференциальных уравнений.

Примеры.

1) Найти векторную линию поля , проходящую через точку (1;0;0)

Решение.

Дифференциальные уравнения векторных линий будут такими: