1 ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ
Во время решения инженерных задач, в вычислительных устройствах, расчеты, как правило, производятся над приближенными исходными данными. Поэтому главное грамотно организовать вычисления, чтобы обеспечить заданную точность вычислений.
Погрешности вычислений могут быть разбиты на следующие группы:
а) погрешности модели – связанные с физическими допущениями, не контролируемые в процессе численного решения;
б) погрешности исходных данных – при измерениях;
в) погрешность приближенного метода – возникает при численном решении задачи, где точный оператор заменяется приближенным, требующим меньшего количества операций. (Интеграл заменяют суммой, функцию многочленом и т.д.);
г) вычислительная погрешность – в результате вынужденного округления чисел (количество допустимых разрядов в ЭВМ).
Погрешности первых двух видов относятся к неустранимым. Их учитывают при выборе метода решения.
В связи с этим необходимо:
а) оценивать точность результата по известной точности исходных данных;
б) определять точность исходных данных, обеспечивающих заданную точность результата;
в) согласовывать точность различных данных, чтобы не тратить время на один набор данных, если второй – более груб;
г) строить алгоритм вычислений так, чтобы обеспечить требуемую точность более рациональным путем.
1.1 АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ
Абсолютная погрешностьприближенного числа а – это число
, (1.1.1)
где А – точное значение некоторой величины.
На практике чаще всего пользуются предельной абсолютной погрешностью Δа.
, (1.1.2)
где Δа – оценка сверху для Δ.
Основной характеристикой
точности будет являться относительная погрешность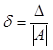 
и, аналогично, 
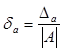- она характеризует
качество приближения, (безразмерная величина обычно измеряется в %).
1.2 ЗАПИСЬ ПРИБЛИЖЕННЫХ ЧИСЕЛ
Пусть приближенное число записано в виде конечной дроби
а = αm·10 m + αm - 1·10 m – 1 + …+ αm – n + 1·10 m – n + 1(1.2.1)
где (αm ≠ 0) и αi = {0, 1... 9}.
Значащими цифраминазывают все цифры в записи числа, начиная с первой ненулевой цифры слева. Например: а = 0,0503, b = 0,00630500. Значащую цифру называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре. В противном случае – цифра считается сомнительной.
Например: Если а = 0,0503 и Δа = 0,00002 или b = 0,00630500 и Δb = 0,000008. (В данном случае подчеркнуты верные цифры).
Если исходное число имеет несколько сомнительных чисел, то его надо предварительно округлить.
Правило округления: чтобы округлить число до n – значащих цифр, отбрасывают все его цифры, стоящие после n – ой значащей или (если это необходимо для сохранения разрядов) заменяют их нулями. При этом:
а) если первое из отбрасываемых чисел меньше 5, то оставшиеся десятичные знаки сохраняют без изменений;
б) если больше 5, то к последней сохраненной цифре добавляют 1.
в) если равно 5, то возможны 2 случая:
1) после 5 идут ненулевые цифры – последняя оставленная увеличивается на 1
2) если первая из отброшенных 5 и далее идут нули, то последняя оставленная цифра увеличивается на 1, если она нечетная и остается прежней, если она четная.
Например: b = 0,125168 ≈ 0,125; π = 3,14159265 ≈ 3,1416;
b = 0,125168 ≈ 0,13; с = 1,25000 ≈ 1,2 d = 1,3500 ≈ 1,4.
Если приближенные числа не носят окончательного характера, то следует сохранять в них одну или две сомнительные цифры до окончания вычислений. При этом абсолютная погрешность меньше половины единицы оставленного разряда.
≤ 0,5 · 10 m – n + 1 (1.2.2)
1.3 ПОГРЕШНОСТИ ФУНКЦИЙ
Пусть задана дифференцируемая функция y = f(x1, x2, …xn), где каждый аргумент определяется с погрешностями Δхі. Тогда абсолютная погрешность функции
Δy = │f(x1 + Δ x1; x2 + Δ x2; …; xn + Δ xn) - f(x1, x2, …xn)│. (1.3.1)
Если предположить, что Δхі → 0, то можно считать
Δ ≈ │df(x1, …xn)│=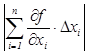 
£ 
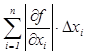(1.3.2)
Отсюда определим верхнюю границу для Δy.
Δy = 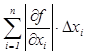, (1.3.3)
где Δхі – предельные абсолютные погрешности для хі., а Δy – предельные абсолютные погрешности для y.
Тогда относительная погрешность
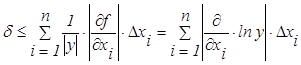. (1.3.4)
Поэтому предельная относительная погрешность
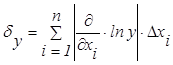. (1.3.5)
Пример. Найти предельные абсолютную и
относительную погрешности объема шара 
если
d = 3,7±0,05 см., а π ≈3,14.
Вычисляем первые частные производные
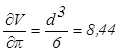и 
,
тогда 
=8,44×0,0016+21,5×0,05=1,088»1,1 (см3) тогда V ≈ 27,4 см3 ± 1,1 см3
и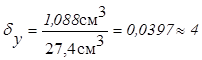 
%.
Применяя эти формулы можно получить следующие правила вычисления погрешностей результата через погрешности компонент:
а) предельная абсолютная погрешность суммы или разности равна сумме предельных абсолютных погрешностей слагаемых;
б) предельная относительная погрешность не превосходит наибольшей из предельных относительных погрешностей слагаемых;
в) предельная относительная погрешность произведения и частного равна сумме предельных относительных погрешностей компонент;
г) предельная относительная погрешность n-ой степени в n раз больше предельной относительной погрешности данного числа (верно и для целых и для дробных n).
1.4 ОБРАТНАЯ ЗАДАЧА ТЕОРИИ ПОГРЕШНОСТЕЙ
Каковы должны быть
погрешности аргументов функции, чтобы абсолютная погрешность функции не
превышала заданной величины. Эта задача решается однозначно только для функции
одной переменной. y = f(x), тогда если f(x) – дифференцируема и f ´(x) ≠ 0, то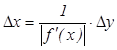 
.
В случае нескольких переменных нужно вводить дополнительные ограничения.
Например, принцип равных влияний – предполагается, что в формуле (1.3.3) все слагаемые равны и следовательно
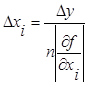
. (1.4.1)
Пример №1. С какой точностью нужно измерить угол x в первой четверти, чтобы получить значение sin x c пятью верными знаками (0° ≤ x ≤ 60°).
Решение: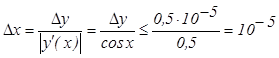 
, так как 0,5 < cos x < 1 в заданном промежутке.
Пример №2. Радиус основания цилиндра R ≈ 2 м. Н ≈ 3 м. – высота. С какой точностью надо определить R и Н, чтобы его объем можно было вычислить с точностью до 0,1 м3.
Решение: V = π R2H и ΔV = 0,1 м3. Для значений R = 2 м. Н = 3 м. π = 3,14 получим приближенно:
.
На основании "принципа равных влияний аргументов" (число аргументов n = 3) имеем:
.
2 МАТРИЦЫ
2.1 ОСНОВНЫЕ ДЕЙСТВИЯ МАД МАТРИЦАМИ:
а) Сложение (разность).
А ± В = [аij ± bij], (2.1.1)
причем А ±В = В ± А; А ± 0 = 0 ± А = А.
Например: А =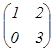 
В
= 
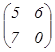тогда А+В=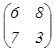
б) Умножение на число.
α ∙А = А ∙ α = [α ∙ аij] (2.1.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
