1.Абсолютная погрешность определяется формулой:
а) 
б) 
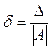в) 
2. Относительная погрешность определяется формулой
а) 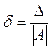б) 
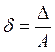в)
3. Какая матрица называется единичной?
а)
б) 
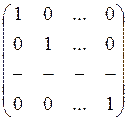в)
4. Укажите действия, которые нельзя выполнять над матрицами
а) ) А±В б) А·В в)А/В
5. Произведение матрицы А на матрицу В есть матрица С элементы которой вычисляют по формуле:
а) сij= ai1 ∙ b1j + ai2 ∙ b2j + … + ain ∙ bnj., б) сij= aii ∙ bjj в) сij= aij ∙ bji,
6. Чтобы сложить или вычесть матрицы нужно
а) А ± В = [аij ± bij], б) А ± В = [аij + bij], в) А ± В = [аij - bij],
7. Матрица А-1 называется обратной к матрице А, если
а) А-1 =-А б) А-1 ·А=Е в) А-1 =1/А
8. Обратную матрицу можно вычислить по формуле
а)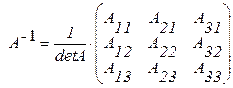 
б)
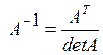в)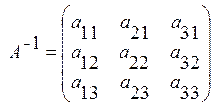 
9. Какая матрица называется вырожденной?
а) у которой 
б) в которой более 2 нулей в)
у которой только 
10. Для каких матриц не существует обратной матрицы?
а) для квадратной б) для симметричной в) для вырожденной
11. Собственными числами 
и векторами 
матрицы
называются:
а) диагональные элементы матрицы;
б) элементы матрицы и её столбцы; в) число
и вектор, удовлетворяющие уравнению 
12. Что такое размерность матрицы?
а) Число её строк б) Число её столбцов в) число её строк×число её столбцов.
13. У двух подобных матриц А и В…
а) det B = det A; б) совпадают наборы собственных чисел в) det B = det A; и совпадают наборы собственных чисел
14. Матрица называется ортогональной, если
а) QТ ∙ Q = Е или QТ = Q-1 б) если она квадратная в) если существует Q-1
15. К точным методам решения систем линейных уравнений относятся
а) метод Крамера б) метод простой итерации в) метод Зейделя
16. К приближенным методам решения систем линейных уравнений относятся
а) метод Крамера б) метод простой итерации в) матричный метод.
17. К точным методам решения систем линейных уравнений относятся
а) метод Гаусса б) метод простой итерации в) метод Зейделя
18. К приближенным методам решения систем линейных уравнений относятся
а) метод Крамера б) метод Зейделя в) матричный метод.
19. Каким методом можно решать вырожденные системы линейных уравнений?
а) методом Крамера б) методом Гаусса в) матричным методом
20. Метод Крамера решает …
а) системы линейных уравнений б) системы нелинейных уравнений в) системы дифференциальных уравнений
21. Метод Гаусса решает …
а) системы линейных уравнений б) системы нелинейных уравнений в) системы дифференциальных уравнений
22. Матричный метод решает …
а) системы линейных уравнений б) системы нелинейных уравнений в) системы дифференциальных уравнений
23. Метод главных элементов решает …
а) системы линейных уравнений б) системы нелинейных уравнений в) системы дифференциальных уравнений
24. Метод простой итерации решает …
а) системы линейных уравнений б) системы интегральных уравнений в) системы дифференциальных уравнений
25. Метод Зейделя решает …
а) системы интегральных уравнений б) системы линейных уравнений в) системы дифференциальных уравнений
26. Условием сходимости метода простой итерации для систем линейных уравнений является
а) норма преобразованной матрицы должна быть < 1 б) норма исходной матрицы должна быть < 1 в) норма преобразованной матрицы должна быть <0
27. Условием сходимости метода простой итерации для систем линейных уравнений является
а) наличие «диагонального предпочтения» б) наличие 0 на главной диагонали в) невырожденность матрицы
28. Метод Крылова позволяет определить
а) собственные числа и векторы матрицы А б) решение краевой задачи в) разложение функции в ряд.
29. Можно ли при помощи итерационного метода одновременно определить набор собственных чисел и векторов матрицы А?
а) да, для симметричных, положительноопределённых матриц б) нет в) да, для любой матрицы
30. Метод скалярных произведений позволяет найти..
а) наибольшее по модулю собственное число и соответствующий ему собственный вектор б) все собственные числа матрицы в) угол между собственными векторами.
31. для чего используется QR алгоритм?
а) Для отыскания собственных чисел и векторов матрицы б) для решения задачи Коши в) для интерполирования.
32. Какое условие определяет наличие корня нелинейного
уравнения внутри интервала 
а) 
б)
в) 
33. Метод половинного деления позволяет определить
а) наибольшее по модулю собственное число матрицы; б) решение краевой задачи; в) корень нелинейного уравнения.
34. Метод касательных (Ньютона) позволяет определить
а) наибольшее по модулю собственное число матрицы; б) решение краевой задачи; в) корень нелинейного уравнения.
35. Метод хорд позволяет определить
а) наибольшее по модулю собственное число матрицы; б) решение краевой задачи; в) корень нелинейного уравнения.
36. Метод секущих позволяет определить
а) наибольшее по модулю собственное число матрицы; б) решение краевой задачи; в) корень нелинейного уравнения.
37. Комбинированный метод хорд и касательных позволяет определить
а) наибольшее по модулю собственное число матрицы; б) решение краевой задачи; в) корень нелинейного уравнения.
38. Метод половинного деления можно применять к нелинейным
уравнениям 
у которых:
а) б)
в)
к любым уравнениям.
39. Метод касательных (Ньютона) можно применять к нелинейным
уравнениям у которых:
а) б) , а производные и не меняют знака на; в) к
любым уравнениям.
40. Метод секущих можно применять к нелинейным уравнениям у которых:
а) б) , а производные и не меняют знака на; в) к
любым уравнениям.
41. Метод хорд можно применять к нелинейным уравнениям у которых:
а) б) , а производные и не меняют знака на; в) к любым
уравнениям.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
