42. Комбинированный метод хорд касательных можно применять к
нелинейным уравнениям 
у которых:
а) 
б) 
, а производные 
и не меняют знака на
; в) к любым
уравнениям.
43. Итерационная формула для метода касательных имеет вид:
а)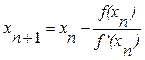 
б) 
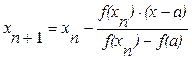в)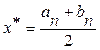 
44. Итерационная формула для метода хорд имеет вид:
а) 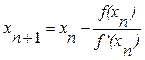б)
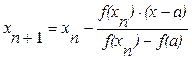в)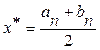
45. Какое условие определяет выбор стартовой точки для метода касательных?
а) 
б) 
в)
средняя точка интервала
46. Какое условие определяет выбор стартовой точки для метода хорд?
а) б) в) средняя точка интервала
47. Какой метод сходится быстрее
а) метод половинного деления; б) метод касательных; в) комбинированный метод хорд и касательных?
48. Какая встроенная функция Mathcad позволяет находить корни нелинейного уравнения?
а)root(f(x),x); б) rkfixed(y,a,b,N,D) в) никакая.
49. Метод Ньютона (обобщённый метод касательных) решает …
а) системы линейных уравнений б) системы нелинейных уравнений в) системы дифференциальных уравнений
50. При каких условиях систему нелинейных уравнений 
можно
решать методом простой итрации?
а) если отображение 
является сжимающим; б) если отображение является взаимообратным;
в) если отображение является
непрерывным
51. Сжимающим называется отображение , которое удовлетворяет
условию
а) 
при некотором 
б)
в) 
52. Что является достаточным признаком сходимости метода простой итерации для системы нелинейных уравнений?
а) норма матрицы Якоби 
б)
все функции в системе – непрерывны; в) система уравнений имеет «диагональное
предпочтение».
53. Какое условие является критерием близости функции y(x) для интерполяции полиномом g(x)?
а) 
в узловых точках б) похожий внешний вид
функции в) совпадение
их значений в граничных точках интервала.
54. Интерполяционный полином Лагранжа имеет вид:
а)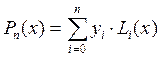 
б) 
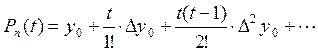в)
55. Что такое « базис Лагранжевых коэффициентов» для полинома Лагранжа?
а) набор произвольнгых постоянных; б) многочлены степени n, для которых
верно условие 
в) тригонометрические
функции.
56. Преимущество полинома Лагранжа состоит в том, что…
а) « базис Лагранжевых коэффициентов» рассчитывается для системы точек, а значит пригоден для описания любой функции заданной на этом множестве; б) выглядит «короче» полинома Ньютона; в) может описывать функцию на всей числовой прямой.
57. Недостаток полинома Лагранжа состоит в том, что…
а) нельзя улучшить точность вычислений без пересчёта « базиса Лагранжевых коэффициентов»; б) не использует конечные разности; в) недостатков не имеет.
58. Схема Эйткена реализует:
а) один из вариантов построения полинома Лагранжа, в котором можно добавлять узлы интерполяции; б) схему решения системы линейных уравнений; в) схему деления многочленов.
59.Преимущество схемы Эйткена состоит в том, что…
а) можно улучшить точность вычислений без пересчёта « базиса Лагранжевых коэффициентов»; б) не использует конечные разности; в) может описывать функцию на всей числовой прямой.
60. Построение интерполяционного полинома Ньютона основано на понятии…
а) разделённых и конечных разностей; б) непрерывности функции в) неопределенных коэффициентов.
61. Интерполяционный полином Ньютона имеет вид:
а) 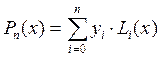б)
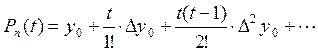в)
62. Выберите формулу интерполяционного полинома Ньютона для интерполяции «назад»
а) 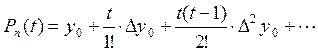б)
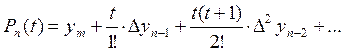в)
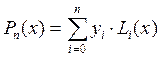
63. Выберите формулу интерполяционного полинома Ньютона для интерполяции «вперёд»
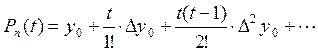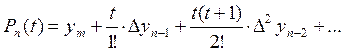а) б) в)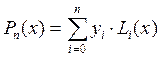
64. Что такое «сплайн»?
а) гибкая линейка; б) функция, которая на каждом из отрезков [хi,хi+1] является многочленом степени m и удовлетворяет условиям непрерывности производных до порядка m-1 включительно в узлах интерполяции; в) результат вычисления интеграла.
65. Что такое «задача Коши для обыкновенного дифференциального уравнения»?
а) задача отыскания частного решения, соответствующего начальным условиям; б) отыскания общего решения. в) отыскание частного решения.
66. Какую задачу решает метод Эйлера?
а) задачу Коши для обыкновенного дифференциального уравнения, б) краевую задачу для обыкновенного дифференциального уравнения; в) Задачу отыскания собственных значений.
67. На чем основан метод Эйлера?
а) на разложении решения в ряд Тейлора; б) на интегрировании функций в явном виде; в) на методах линейной алгебры.
68. Для чего выполняется «двойной пересчет» в ходе решения задачи Коши приближёнными методами?
а) для определения точности вычислений; б) для получения решения на более длинном промежутке; в) для изучения свойств функции.
69. Какой порядок точности имеет метод Эйлера?
а) первый; б) второй; в) четвёртый.
70. Какой порядок точности имеют модифицированные методы Эйлера?
а) первый; б) второй; в) четвёртый.
71. Какой порядок точности имеет метод Рунге-Кутта?
а) первый; б) второй; в) четвёртый.
72. Какая встроенная функция MathCad реализует метод Рунге–Кутта четвертого порядка с фиксированным шагом?
а) rkfixed(y,a,b,N,D) б) qr(M) в) root(f(x),x);
73. Что такое краевая задача для дифференциального уравнения
?
а) задача отыскания частного
решения, соответствующего краевым условиям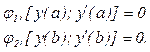 
б)
задача отыскания частного решения, соответствующего начальным условиям; в)
определение значения функции 
74. Какая задача решается при помощи метода конечных разностей?
а) Краевая задача; б) задача Коши в) задача об определении центра масс.
75. Какая задача решается при помощи метода коллокации?
а) Краевая задача; б) задача Коши в) задача об определении центра масс.
76. Какая задача решается методом прямоугольников?
а) вычисление определённого интеграла; б) решение дифференциального уравнения; в) вычисление производной.
77. Какая задача решается методом трапеций?
а) вычисление определённого интеграла; б) решение дифференциального уравнения; в) вычисление производной.
78. Какая задача решается методом Симпсона?
а) вычисление определённого интеграла; б) решение дифференциального уравнения; в) вычисление производной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.