Дослідження функції на монотонність та екстремум. Елементи лінійної та векторної алгебри (Теоретичний матеріал та контрольні завдання зі зразками вирішення з вищої математики)

Оскільки границя k не існує при , то асимптоти графіка функції при  немає.

Розглянемо поведінку функції на нескінченністі при , маємо.

, тобто функція є нескінченно велика при , а це означає, що вона змінюючись стає і залишається за абсолютною величиною більше, ніж будь-яке наперед задане додатне число М, тобто  при , або .

2.7 Дослідження функції на монотонність

та екстремум

Означення 1. Функція називається зростаючою (спадною) на деякому інтервалі (а,b), якщо для будь-яких х₁, х₂, які задовольняють нерівностям , виконана нерівність

  (відповідно ).

Теорема 1  (про достатні умови монотонності)

Якщо  диференційовна на інтервалі (а,b) і  () на (а,b), то функція зростаюча (спадна) на цьому інтервалі.

Означення 2. Точка х₀ називається точкою строгого локального мінімуму (максимуму) функції , якщо при всіх з деякого б-околу точки х₀, тобто , виконується нерівність:

Точки мінімуму та максимуму називаються точками локального екстремуму.

Означення 3. Точки, в яких функція існує, а похідна функції  або не існує, називаються критичними точками.

Проміжки монотонності обмежені критичними точками.

Теорема 2. (необхідні умови екстремуму).

Якщо точка х₀ є точкою екстремуму функції , то в цій точці або , або  не існує.

Тобто точки екстремуму функції слід шукати серед критичних точок першого роду.

Теорема 3. (про достатні умови екстремуму, або достатня ознака екстремуму).

Якщо функція  неперервна в критичній точці першого роду х₀, диференційовна в околі цієї точки і при переході через точку х₀ зліва направо похідна  змінює знак плюс “+” на мінус “-”, то точка х₀ є точка максимуму функції якщо  змінює знак мінус “-” на плюс “+”, то точка  є точка мінімуму.

Порядок дослідження функції на екстремум розглянемо на прикладі.

Приклад 1. Знайти інтервали монотонності і екстремуми функції

Розв’язання.

1). Знаходимо область визначення функції.

2). Знаходимо похідну функції:

Розв’язуючи рівняння , знаходимо критичні точки, які ділять область D(х) на інтервали.

     

       

Отже, інтервали монотонності     

3). Знак похідної в кожному інтервалі визначимо за її знаком у будь-якій точці цього інтервалу, взявши, наприклад,

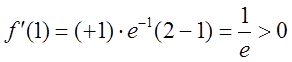
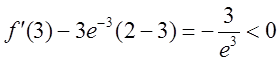
4). На основі відповідних теорем про монотонність і екстремум функції маємо, що функція спадає при  і при , функція зростає при .

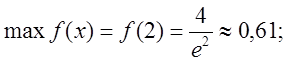
Зауваження: при дослідженні функції на монотонність і екстремум зручно користуватись таблицею.

		0	(0,2)	2	(2,+¥
	-	0	+	0	-
		min 0	­	max 0,61

Розглянемо питання про відшукання найменшого й найбільшого значень неперервної функції на відрізку, тобто задачу знаходження глобального максимуму і мінімуму неперервної функції  на відрізку .

Порядок розв’язання цієї задачі розглянемо на прикладі.

Приклад 2. Знайти найбільше та найменше значення функції  на .

Розв’язання.

1). Знайдемо всі критичні точки функції  .

Дістанемо х₁=0, х₂=2. на даний відрізок попадають обидва корені.

2). Обчислимо значення функції в точках х₁=-1, х₂=0, х₃=2.

 

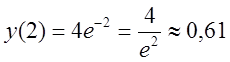
3). Порівнявши локальні екстремуми функції в точках х₂=0, х₃=2із значеннями на кінцях відрізку , знаходимо найбільше значення функції  і найменше значення функції .

Відповідь: М = 2,72 m = 0.

2.8 Інтервали опуклості та угнутості.

Точки перетину кривої

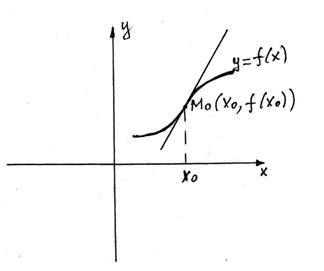Означення 1.Крива називається опуклою (угнутою) в точці, якщо вона розміщена нижче (вище) дотичної до кривої в цій точці. (див. рис. 6).

Рисунок 6

Означення 2. Крива називається опуклою (угнутою) на інтервалі, якщо вона опукла (вгнута) в кожній точці цього інтервалу.

Теорема 1. (про достатні умови опуклості (вгнутості)).

Якщо  двічі диференційовна на інтервалі (а,b) і  на (а, b), то графік функції на цьому інтервалі опуклий (угнутий).

Означення 3. Точка х₀ називається точкою перетину графіка функції , якщо в ній опуклість змінюється на вгнутість, або навпаки.

Означення 4. Точки, в яких функція існує, а друга похідна  функції  або не існує, називається критичними точками другого роду.

Теорема 2. (необхідні умови опуклостей вгнутостей).

Якщо точка х₀ є точкою перетину графіка функції , то в цій точці або , або не існує.

Тобто точки перетину графіка функції слід шукати серед критичних точок другого роду.

Теорема 3. (про достатні умови опуклості, вгнутості або достатня ознака точки перетину).

Якщо функція неперервна в критичній точці х₀, двічі диференційовна в околі цієї точки і при переході через точку х₀ друга похідна змінює знак, то х₀ – абсциса точки перетину  графіка функції .

Зауваження. Опуклість, угнутість, точки перетину графіка функції знаходяться точка так, як і монотонність та екстремум, тільки по другій похідній.

Порядок дослідження функції на існування точок перетину розглянемо на прикладі.

Приклад. Знайти інтервали опуклості та вгнутості і точки перетину кривої

Розв’язання.

1). Знаходимо область визначення функції

2). Знаходимо похідну функції

3). Знаходимо другу похідну функції.

Розв’язуючи рівняння , знаходимо критичні точки другого роду, які ділять область D(х) на інтервали.

            

Отже, інтервали:

угнутості , оскільки

опуклості  оскільки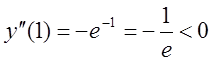

угнутості  оскільки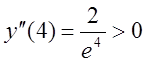

Точки перетину:            

    отже

Зауваження. При дослідженні графіка функції на опуклість та угнутість, на існування точок перетину зручно користуватись таблицею:

х		0,6		3,4
	+	0	-	0	+
у	=	перетин 0,2	?	перетин 0,38	=

2.9 Дослідження поведінки функції та

побудова графіків

Диференціальне числення дає змогу об’єктивно відтворити графік функції із збереженням його характерних особливостей. При дослідженні графіка функції в цілому рекомендується , наприклад, така загальна схема.

1. Знайти область визначення функції, її точки розриву й проміжки неперервності.

2. Перевірити функцію на періодичність, парність, непарність. У разі необхідності знайти характерні точки графіка, наприклад, точки перетину з координатними вісями.

3. Знайти асимптоти функції та з’ясування поведінку функції на границях області визначення.

4. Знайти точки локального екстремуму та інтервали монотонності.

5. Знайти точки перетину, інтервали опуклості та вгнутості.

6. Здобуті дані звести в таблицю, з якої можна дістати інтервали монотонності та опуклості чи угнутості, а також точки екстремуму та перетину (заповнивши відповідні клітини знаками похідних функцій).

7. Побудувати графік функції.

Зауваження. Порядок дослідження доцільно обирати згідно з особливостями функції. При розв’язанні конкретної задачі окремі пункти можна дещо розширити, а деякі можуть виявитися зайвими.

Приклад. Дослідити функцію  і побудувати її графік.

Розв’язання.

Одержані дані в попередніх прикладах зведемо в загальну таблицю.

х		0		0,6		2		3,4
	-	0	+	+	+	0	-	-	-
	+	+	+	0	-	-	-	0	+
	(	min 0	&	перетин 0,20	&	max 0,61	(	перетин 0,38	(