Маємо головний визначник системи:
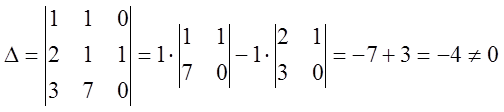
Знайдемо побічні визначники:
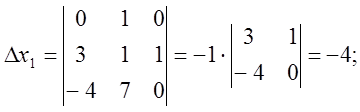
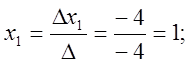
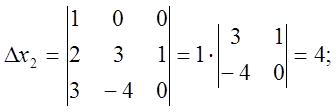
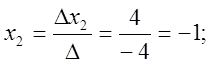
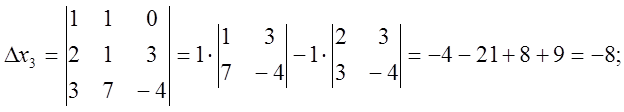
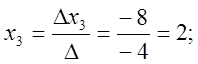
Отже, ![]()
![]()
![]()
3.3 Метод Гауса послідовного
виключення невідомих
В основу методу Гауса покладені елементарні перетворення систем. Цей метод послідовних вилучень невідомих розглянемо на прикладі СЛА Р-3.
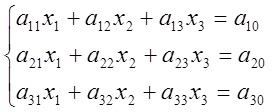 (1)
(1)
Будемо вважати, що визначник системи ![]() і
і ![]() (в
противному разі можна переставити місцями рівняння системи). Один із алгоритмів
методу Гауса полягає в покроковому виконанні таких перетворень.
(в
противному разі можна переставити місцями рівняння системи). Один із алгоритмів
методу Гауса полягає в покроковому виконанні таких перетворень.
1 крок. Вилучаємо х1 з другого, третього рівнянь системи (1). Для цього поділимо перше рівняння на а11. Отримане рівняння помножимо на а21 і віднімемо від другого, потім його ж помножимо на а31 і віднімемо від третього. Дістанемо перетворену систему.
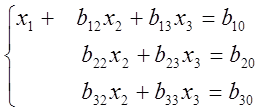 (2)
(2)
де 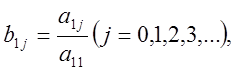
![]()
2 крок. У системі (2) вилучаємо х2 з третього рівняння
системи. При цьому перше рівняння залишаємо без зміни і друге поділимо на ![]() . Отримане рівняння помножимо на b32 і віднімемо
від третього.
. Отримане рівняння помножимо на b32 і віднімемо
від третього.
Після цього матимемо систему
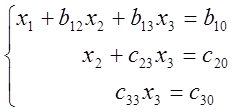 (3)
(3)
де 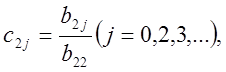
![]()
Зведення системи (1) до трикутного вигляду (3) називають прямим ходом методу Гауса. Обернений хід методу Гауса полягає в обчисленнях невідомих за формулами (4).
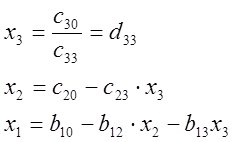 (4)
(4)
Отримані результати можна узагальнити у вигляді теореми:
Теорема.
Якщо в процесі перетворень Гауса з’явиться рівняння виду ![]() , то вихідна система несумісна. Якщо
вона зводиться до трикутного вигляду, то ця система визначена, а якщо – до
трапецоїдного, то система невизначена. Або має безліч розв’язків.
, то вихідна система несумісна. Якщо
вона зводиться до трикутного вигляду, то ця система визначена, а якщо – до
трапецоїдного, то система невизначена. Або має безліч розв’язків.
Приклад. Розв’язати систему методом Гауса.
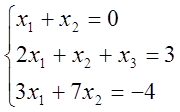 (1)
(1)
Розв’язання.
Запишемо систему у вигляді.
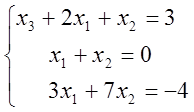 (2)
(2)
Таким чином, перший крок для системи (2) виконувати не треба.
2 крок. У системі (2) вилучаємо невідому х2 з третього рівняння системи. При цьому перше і друге рівняння залишаємо без змін. Отримане друге рівняння помножимо на 3 і віднімемо від третього. Дістанемо перетворену систему:
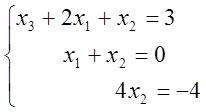 (3)
(3)
звідки за допомогою оберненого ходу методу Гауса маємо
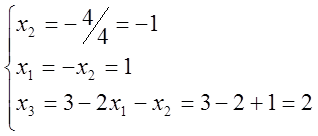
Оскільки система (1) звелася до трикутного вигляду (3), вона визначена, тобто має єдиний розв’язок:
![]()
![]()
![]()
Зауваження. Якщо формули Крамера застосовують, як правило, для ![]() , то метод Гауса для
, то метод Гауса для ![]() . Він може бути використаний при
розв’язанні системи т рівнянь з n невідомими
. Він може бути використаний при
розв’язанні системи т рівнянь з n невідомими ![]() і не потребує попереднього
розгляду питання про сумісність системи.
і не потребує попереднього
розгляду питання про сумісність системи.
3.4 Вектори, основні поняття та означення
Усі фізичні величини поділяються на скалярні (температура, маса, робота), які зображаються одним числом, векторні (сила, швидкість, прискорення тощо), які зображаються матрицею-стовпцем з певною кількістю елементів, тензорні (деформація, напруження тощо), які зображаються квадратною матрицею.
Якщо вектор можна переносити паралельно самому собі, то його називають вільним, або геометричним. Якщо вектор жорстко зв’язаний з точкою прикладання, то він називається зв’язаним. Прикладом такого вектора є вектор сили, радіус – вектор точки.
Означення 1. Вектором називається впорядкована пара точок ![]() ,перша
з яких називається початком вектора. Друга – його кінцем, тобто є спрямований
відрізок і позначається або
,перша
з яких називається початком вектора. Друга – його кінцем, тобто є спрямований
відрізок і позначається або ![]() , або
, або ![]() .
.
Означення 2. Відстань між M i N називається довжиною або модулем вектора
і називається 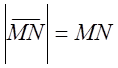 , або
, або ![]() .
.
Означення 3. Два вектори називаються колінеарними, якщо вони розташовані на одній прямій або на двох паралельних прямих.
Означення 4. Два вектори називаються рівними, якщо вони колінеарні, мають однакову довжину і однаково направлені.
Означення 5. Вектор, модуль якого дорівнює одиниці, називається одиничним, або
ортом ![]() ,
, ![]()
Вектор, у якого початок і кінець збігаються, називається нульовим, його модуль дорівнює нулю.
Означення 6. Вектор називається вільним, якщо
1) він повністю визначається модулями і напрямом![]()
2) його можна переносити паралельно самому собі, беручи за початок вектора довільну точку простору.
3.5 Лінійні операції з векторами. Базис
Означення 1. Лінійними називаються додавання двох векторів, віднімання та множення вектора на скаляр (число), тобто
1) ![]() , 2)
, 2) ![]()
Означення 2. Сумою двох неколінеарних векторів називають вектор, який виходить з їх спільного початку і є діагоналлю паралелограма, побудованого на даних векторах, як на сторонах.
З цього правила паралелограма випливає правило трикутника.
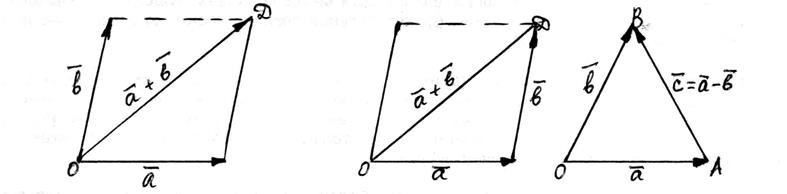 |
Рисунок 9
Означення 3. Різницею ![]() називають такий вектор
називають такий вектор ![]() , який слід додати до
, який слід додати до ![]() , щоб отримати
, щоб отримати ![]() , тобто
, тобто ![]() ,
якщо
,
якщо ![]() .
.
Таким чином, в паралелограмі (мал..
9), побудованому на векторах ![]() і
і ![]() , одна вектор – діагональ
, одна вектор – діагональ ![]() - є сумою, а друге
- є сумою, а друге ![]() є різницею даних векторів.
є різницею даних векторів.
Зауваження. Якщо додатків більше ніж два, то маємо правило многокутника або замикання ломаної.
Означення 4. Добутком вектора ![]() на числа
на числа ![]() називається вектор
називається вектор
![]() ,
який:
,
який:
1) має модуль, що дорівнює модулю вектора ![]() ,
помноженого на абсолютне значення числа
,
помноженого на абсолютне значення числа ![]() ,
тобто
,
тобто
![]()
2) колінеарний з вектором ![]() ,
, ![]() ,
,
3) однаково напрямлений з вектором ![]() ,
якщо
,
якщо ![]() , протилежно напрямлений, якщо
, протилежно напрямлений, якщо ![]() .
.
Зокрема, вектор ![]() називається протилежним до вектора
називається протилежним до вектора ![]() і називається
і називається ![]() , тобто
, тобто
![]()
![]() .
.
Означення 5. Ортом ![]() вектора
вектора ![]() називається одиничний вектор того самого
напряму, що й вектор
називається одиничний вектор того самого
напряму, що й вектор ![]() , тобто
, тобто
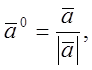 або
або ![]() .
.
Це є формула орта ![]() , або операція нормування вектора
, або операція нормування вектора ![]() .
.
Властивості лінійних операцій
1. ![]() -
комутативний (переставний) закон.
-
комутативний (переставний) закон.
2. ![]() -
асоціативний (сполучний) закон.
-
асоціативний (сполучний) закон.
3. ![]() -
дистрибутивний (розподільний) закон множення відносно додавання.
-
дистрибутивний (розподільний) закон множення відносно додавання.
4. ![]() -
дистрибутивний закон додавання відносно множення.
-
дистрибутивний закон додавання відносно множення.
5. ![]() -
асоціативний закон відносно множення.
-
асоціативний закон відносно множення.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.