Означення 1.Нехай a(х) і b(х) нескінченно малі в точці х0, тоді
1)
якщо 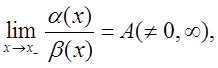 то
то
aіb називаються нескінченно малими одного порядку
при ![]() .
.
2)
Якщо 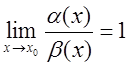 ,
то aіbназиваються еквівалентами нескінченно малими . Еквівалентність
нескінченно малих коротко позначається так:
,
то aіbназиваються еквівалентами нескінченно малими . Еквівалентність
нескінченно малих коротко позначається так:
a ~ b, х®х0
3)
Якщо 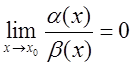 , то aназивається
нескінченно малою вищого порядку порівняно з b(х) при
х®х0.
, то aназивається
нескінченно малою вищого порядку порівняно з b(х) при
х®х0.
4)
Якщо 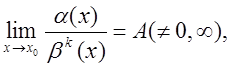 де kÎN, то aназивається нескінченно малою k–того порядку відносно b.
де kÎN, то aназивається нескінченно малою k–того порядку відносно b.
Для нескінченно великих функцій діють аналогічні правила порівняння. При знаходженні границі частки двох нескінченно малих (великих) у багатьох випадках корисна теорема:
Теорема 1. Якщо a(х) ~ a1(х), b(х) ~ b1(х), х®х0 і існує
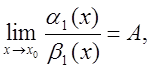 то
існує і
то
існує і 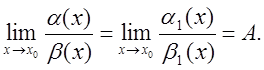
Таблиця еквівалентних нескінченно малих (a® 0).
1. sina ~ a6. ln (1+a) ~ a
2. tga ~ a7. aa - 1 ~ alna
3. arcsina ~ a8. е2 – 1 ~ a
4. arctga ~ a9. (1+a)m - 1~ ma
5. ![]() ~
~ ![]() 10. loga (1+a) ~ a
10. loga (1+a) ~ a![]()
Приклади.
1. 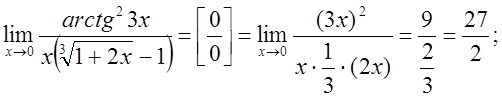
2. 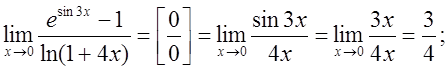
1.6 Неперервність і точки розриву функції
Означення 1. Функція f(x), визначена в деякому околі точки х0, називається неперервною в точці х0, якщо виконується рівність
![]() (1)
(1)
Оскільки ![]() , то умову
неперервності можна подати у вигляді
, то умову
неперервності можна подати у вигляді
![]()
тобто для неперервної функції знаки функції та її границі можна міняти місцями.
Величина Dх = х – х0 називається приростом аргументу, а Dу = f(x0+Dx)-f(x0) – приростом функції у точці х0. У цих позначеннях рівність (1) має вигляд
limDy = 0(2), тобто
Dх ® 0
Означення 2. Функція f(x) називається неперервною в точці х0, якщо її приріст у цій точці є нескінченно мала функція при Dх ® 0.
Теорема 1. Для неперервності функції f(x) в точці х0 необхідно й достатньо, щоб вона була неперервна в цій точці зліва й справа, тобто
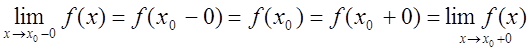 (3)
(3)
Означення 3. Функція f(x) неперервна в точці х0 тоді й тільки тоді, коли вона неперервна в цій точці зліва і справа і виконується рівність:
![]()
Якщо хоч одна з цих умов порушується, то кажуть, що х0 – точка розриву функції.
Означення 4. Точка розриву х0 функції f(x) називається точкою розриву І роду, якщо в ній існують односторонні границі. При цьому:
а) якщо f(x0 + 0) = f(x0 - 0)¹f(x0), то кажуть про точку усувного розриву![]()
б) якщо f(x0 + 0) ¹f(x0 - 0)= f(x0), то кажуть про точку стрибка функції.
Означення 5. Точка розриву x0 функції f(x) називається точкою розриву ІІ-го роду, якщо в ній не існує принаймні одна з односторонніх границь.
Приклад. Дослідити функцію 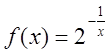 нанеперервність, встановити характер точок розриву.
нанеперервність, встановити характер точок розриву.
Дана функція є елементарною як суперпозиція двох елементарних функцій і визначена "х ÎR, крім х = 0. У точці х = 0 функція не визначена. Знаходимо
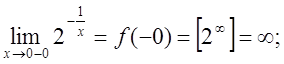
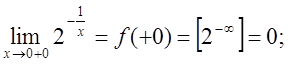
Таким чином, згідно з класифікацією розривів точка х = 0 є точкою розриву другого роду. (див. на рис. 4).
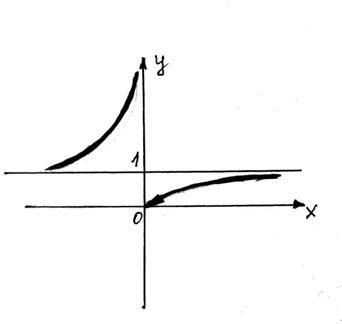 |
Рисунок 4
1.7 Запитання для самоперевірки
1. Які числові множини ви знаєте?
2. Дайте означення функції, області визначення і множини значень функції.
3. Які функції мають обернену? Як розташовані на площині графіки взаємно обернених функцій?
4. Дайте означення парної і непарної, монотонно зростаючої і спадної функції.
5. Назвіть основні елементарні функції та властивості цих функцій.
6. Дайте означення складної функції та наведіть приклади елементарних функцій.
7. Як побудувати графіки функцій y=Af(ax+b)+c; y=|f(x)|.
8.
Дайте означення границі
функції ![]() нескінченно малої і нескінченно великої
величини.
нескінченно малої і нескінченно великої
величини.
9. Сформулюйте властивості нескінченно малої і нескінченно великої величини.
10. Сформулюйте теореми про границі, назвіть дві важливі границі і наслідки з них.
11. Дайте означення еквівалентних нескінченно малих величин, запишіть таблицю еквівалентних.
12. Дайте два означення неперервності функції в точці.
13. Як класифікуються точки розриву? Наведіть приклади.
1.8 Завдання для самостійної роботи
Зміст роботи
1. Знайти область визначення функції.
2. Перевірити парною чи непарною є дана функція.
3. Знайти період функції.
4. Побудувати графіки функції а), б), в).
5. Обчислити (без правила Лопіталя) границі.
6. Дослідити на неперервність функції а), б) та побудувати їх графіки.
Варіант 1.
1. ![]() 2.
2. ![]() 3.
3.
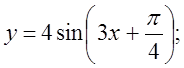
4. а) ![]() б)
б) 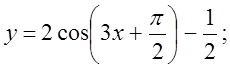 в)
в)
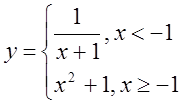
5. а) 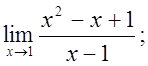 б)
б) 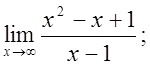 в)
в)
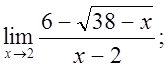
г) 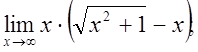 д)
д) 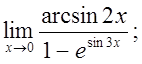 e)
e) 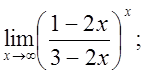
ж) 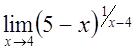
6. а) 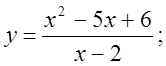 б)
б) 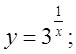 в)
в) 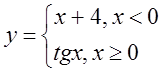
Варіант 2.
1. 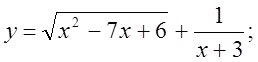 2.
2. ![]() 3.
3.
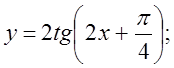
4. а) ![]() б)
б) 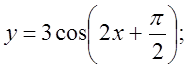 в)
в)
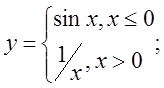
5 а) 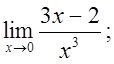 б)
б) 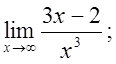 в)
в)
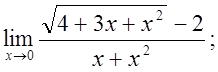
г) 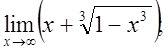 д)
д) 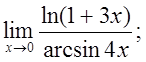 е)
е)
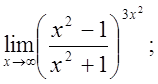
ж) 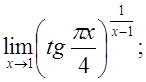
6. а) 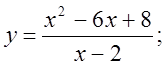 б)
б) 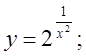 в)
в)
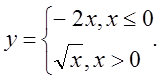
Варіант 3.
1. ![]() 2.
2. ![]() 3.
3.
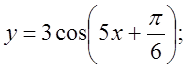
4. а) ![]() б)
б) 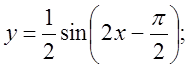 в)
в)
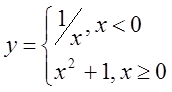
5. а) 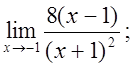 б)
б) 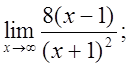 в)
в)
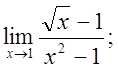
г) 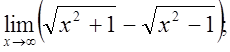 д)
д) 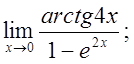 е)
е) 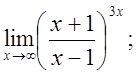
ж) 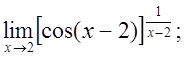
6. а) 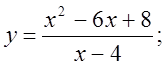 б)
б) 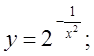 в)
в)
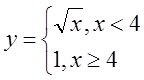
Варіант 4.
1. ![]() 2.
2. ![]() 3.
3.
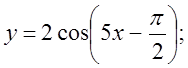
4. а) 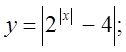 б)
б) 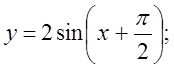 в)
в) 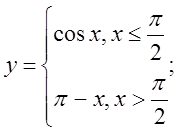
5. а) 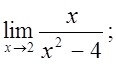 б)
б) 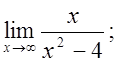 в)
в) 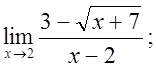
г) 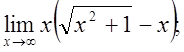 д)
д) 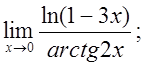
е) 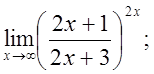 ж)
ж) ![]()
6. а) 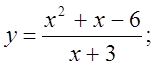 б)
б) 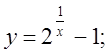 в)
в)
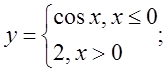
Варіант 5.
1. ![]() 2.
2. ![]() 3.
3.
![]()
4. а) ![]() б)
б) ![]()
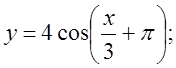 в)
в)
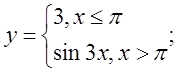
5. а) 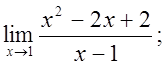 б)
б) 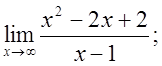 в)
в)
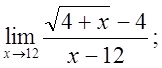
г) 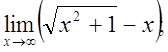 д)
д) 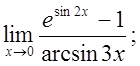
е) 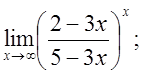 ж)
ж) 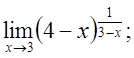
6. а) 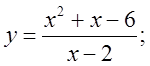 б)
б) 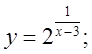 в)
в) 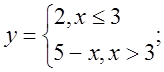
Варіант 6.
1. 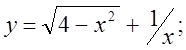 2.
2. 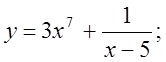 3.
3.
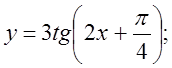
4. а) 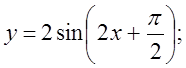 б)
б) 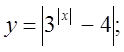 в)
в) 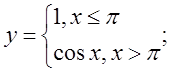
5. а) 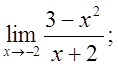 б)
б) 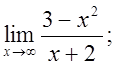 в)
в) 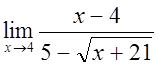
г) 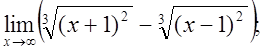 д)
д) 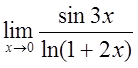 е)
е)
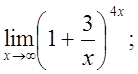
ж) 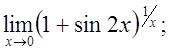
6. а) 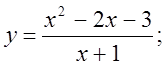 б)
б) 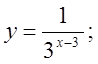 в)
в)
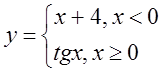
Варіант 7.
1. 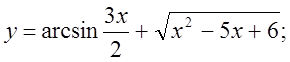 2.
2. ![]() 3.
3.
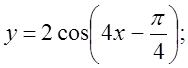
4. а) ![]() б)
б) 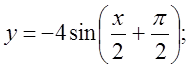 в)
в)
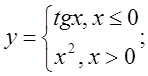
5. а) 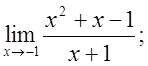 б)
б) 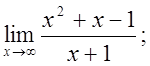 в)
в)
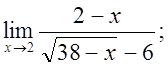
г) 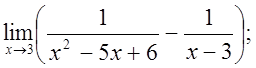 д)
д) 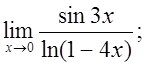
е) 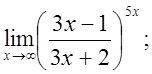 ж)
ж)
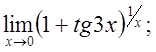
6. а) 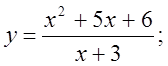 б)
б) 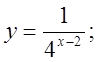 в)
в)
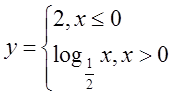
Варіант 8.
1. ![]() 2.
2. ![]() 3.
3.
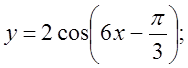
4. а) ![]() б)
б) 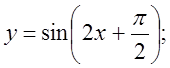 в)
в) 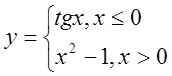
5. а) 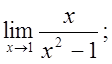 б)
б) 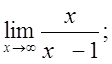 в)
в) 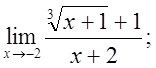
г) 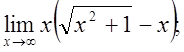 д)
д) 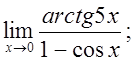
е) 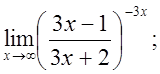 ж)
ж) 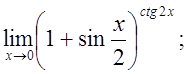
6. а) 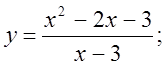 б)
б) 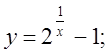 в)
в)
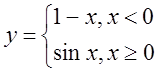
Варіант 9.
1. ![]() 2.
2. ![]() 3.
3.
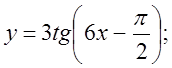
4. а) 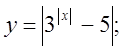 б)
б) 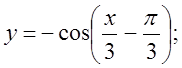 в)
в) 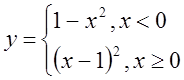
5. а) 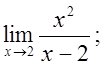 б)
б) 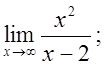 в)
в) 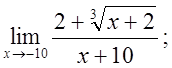
г) 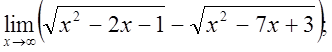 д)
д) 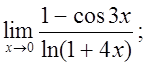
е) 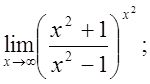 ж)
ж)
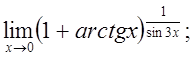
6. а) 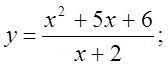 б)
б) 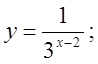 в)
в) 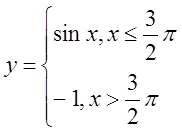
Варіант 10.
1. ![]() 2.
2. ![]() 3.
3.
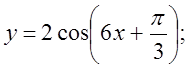
4. а) 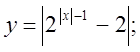 б)
б) 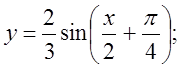 в)
в) 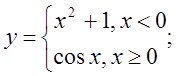
5. а) 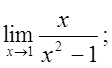 б)
б) 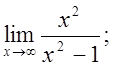 в)
в) 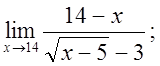
г) 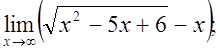 д)
д) 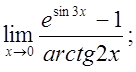
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.