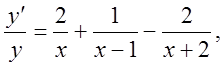
2.3 Диференціал функції та його
геометричний зміст
За
означенням похідної функції ![]() в точці х
приріст функції Dу в точці х має вигляд:
в точці х
приріст функції Dу в точці х має вигляд:
![]() де
де ![]() (1)
(1)
![]() - нескінченно мала вищого порядку
порівняно з Dх.
- нескінченно мала вищого порядку
порівняно з Dх.
Означення 1. Диференціалом функції в точці х називається головна, лінійна відносно Dх частина приросту функції в цій точці і позначається
![]() (2), де
(2), де ![]()
Тобто, завдяки введеному Лейбніцем поняттю диференціала функції (2) похідну функції позначають
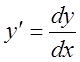 (3)
(3)
і розуміють її як відношення диференціала функції до диференціала аргументу х.
З формул (1) и (2) можна одержати ще один наслідок:
![]() (4),
(4),
тобто, приріст функції наближене дорівнює її диференціалу при досить малих Dх, а значить має місце формула:
![]() (5), де
(5), де ![]()
якою користуються при наближених обчисленнях.
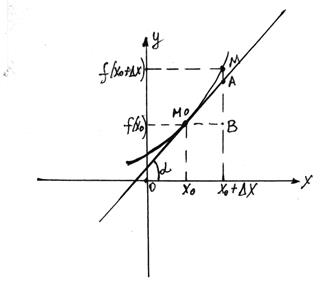
Розглянемо рисунок 5.
![]() - приріст функції.
- приріст функції.
![]() -
диференціал функції
-
диференціал функції
![]() - додаток, в рівності (1), який ми
відкидаємо в наближеної формулі (5).
- додаток, в рівності (1), який ми
відкидаємо в наближеної формулі (5).
Означення. Пряма, яка задається рівнянням.
![]()
![]() (6)
(6)
називається
дотичною до графіка функції ![]() у точці
у точці ![]()
Звідси, геометричний зміст похідної полягає в тому, що кутовий коефіцієнт дотичної в точці М0 дорівнює
![]() (7)
(7)
Означення. Нормаллю до кривої ![]() називається
пряма, перпендикулярна до дотичної в точці дотику М0. Кутовий
коефіцієнт нормалі в точці М0.
називається
пряма, перпендикулярна до дотичної в точці дотику М0. Кутовий
коефіцієнт нормалі в точці М0.
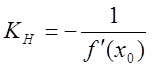
(за умовою перпендикулярності).
Виходячи з
цього можна записати рівняння нормалі в точці ![]() у
вигляду:
у
вигляду:
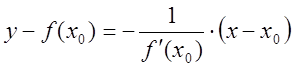 (8)
(8)
Геометричний зміст диференціала функції полягає в тому, що останній являє собою приріст ординати дотичної до даної функції (див. мал. 5).
Диференціал
функції має властивості, аналогічні властивостям похідних. Для довільних
диференційовних функцій ![]() і
і ![]() виконуються рівності
виконуються рівності
![]()
![]()
![]()
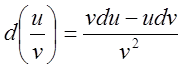
![]()
Важливою є також властивість інваріантності форми диференціала:
![]() або
або ![]() (9)
(9)
тобто форма першого диференціала не залежить від того, чи є аргумент функції F(u) незалежною змінною и, чи є в свою чергу функцією и= и(х) другого аргументу х.
2.4 Похідні та диференціали вищих порядків
Означення. Другою похідною функції ![]() називається похідна
від першої похідної, яка, в свою чергу, є функцією від х, тобто
називається похідна
від першої похідної, яка, в свою чергу, є функцією від х, тобто
![]() або
або 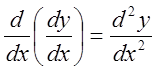
аналогічно,
![]() або
або 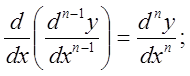
Означення. Функція, що має похідну порядку n на інтервалі (а,b) називається n разів диференційовною на цьому інтервалі.
Наведемо деякі формули для похідних порядку n основних елементарних функцій:
1. ![]()
![]() n Î N
n Î N
2. 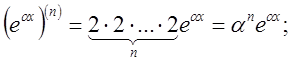
![]()
3. 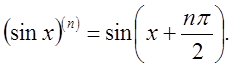
4. 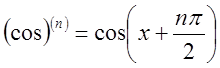
Диференціалом
другого порядку ![]() називається диференціал
від першого порядку цієї функції, тобто
називається диференціал
від першого порядку цієї функції, тобто
![]() або
або ![]()
якщо х – незалежна змінна, то![]() - стала, тобто
- стала, тобто
![]()
Аналогічно,
![]()
Якщо х – не є незалежною змінною, а деякою функцією, то властивості інваріантності форми диференціалів вищих порядків порушується.
Приклад
1. Знайти похідну другого порядку функції ![]()
Розв’язання.
Знайдемо першу похідну
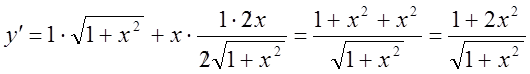
Тепер знайдемо другу похідну
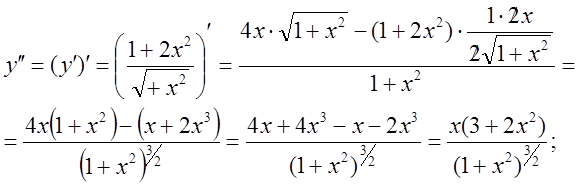
Приклад
2. Знайти похідну другого порядку функції ![]()
Розв’язання.
Послідовно диференціюючи, дістанемо.
![]()
![]()
2.5. Правило Лопіталя та його застосування
Найбільш ефективним методом розкриття невизначеності є правило Лопіталя.
Теорема
Лопіталя. Нехай функції ![]() і
і
![]() диференційовні в околі точки х0
і, крім того, вони є нескінченно малими, тобто
диференційовні в околі точки х0
і, крім того, вони є нескінченно малими, тобто
![]()
причому, ![]() у цьому околі, або
нескінченно великими, тобто
у цьому околі, або
нескінченно великими, тобто
![]()
![]()
тоді границя відношення їх похідних, якщо остання існує і дорівнює А, тобто
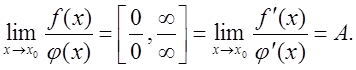
Наслідок
1. Правило Лопіталя
діє також при ![]() ,
, ![]() ,
,
![]() і у випадках однобічних границь,
тобто при
і у випадках однобічних границь,
тобто при ![]()
Наслідок
2. Якщо для похідних ![]() і
і
![]() виконуються умови теореми Лопіталя,
то правило Лопіталя можна застосувати повторно, тобто:
виконуються умови теореми Лопіталя,
то правило Лопіталя можна застосувати повторно, тобто:
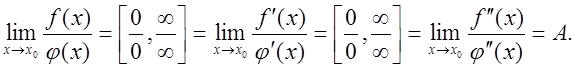
Іноді для розкриття невизначеностей правило Лопіталя доводиться послідовно застосовувати кілька разів.
Приклад
1. Обчислити границю 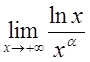
![]()
Розв’язання.
Маємо
невизначеність типу 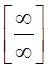 . За правилом Лопіталя
дістаємо
. За правилом Лопіталя
дістаємо 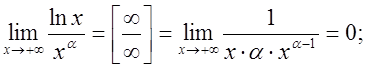
Отже,
логарифмічна функція ![]() при
при ![]() зростає повільніше при
зростає повільніше при ![]() , ніж будь-який додатний степінь
, ніж будь-який додатний степінь ![]() .
.
Приклад
2. Обчислити границю 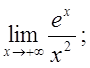
Розв’язання.
Маємо
невизначеність типу 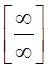 . Застосовуючи правило Лопіталя
двічі, дістанемо:
. Застосовуючи правило Лопіталя
двічі, дістанемо:
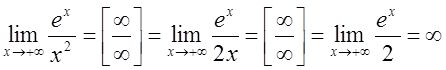
Отже,
показникова функція ах при a>1
зростає швидше при ![]() , ніж будь-який
степінь
, ніж будь-який
степінь ![]() .
.
Наслідок
3. Невизначеності типів ![]() і
і
![]() шляхом простих алгебраїчних
перетворень зводяться спочатку до типів
шляхом простих алгебраїчних
перетворень зводяться спочатку до типів ![]() або
або
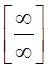 , до яких застосовують правило Лопіталя.
, до яких застосовують правило Лопіталя.
Наслідок
4. Невизначеності типів ![]() ,
,
![]() і
і ![]() ,
які зустрічаються при обчисленні границь функцій вигляду
,
які зустрічаються при обчисленні границь функцій вигляду ![]() , за допомогою тотожності
, за допомогою тотожності
![]()
зводяться спочатку до невизначеності типу ![]() ,
а потім до типів
,
а потім до типів ![]() , або
, або 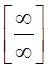 .
.
Приклад
3. Обчислити границю ![]()
Розв’язання
Маємо
визначеність типу ![]() . Подамо у вигляді
. Подамо у вигляді
![]() і розглянемо
і розглянемо
![]() . Зводячи її до типу
. Зводячи її до типу 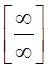 і застосовуючи першу важливу границю
і застосовуючи першу важливу границю 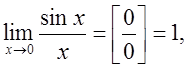 а потім правило Лопіталя, матимемо:
а потім правило Лопіталя, матимемо:
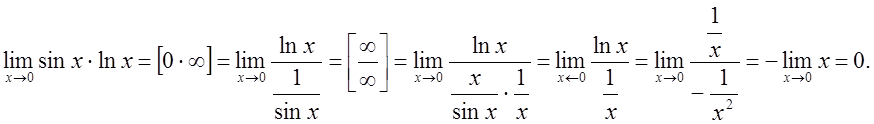
звідси ![]()
2.6 Асимптоти графіка функції
При
вивченні поведінки функції на нескінченності, тобто при ![]() або поблизу точок розриву другого
роду, часто трапляється, що графік функції як завгодно близько наближається до
тієї чи іншої прямої. Ці прямі називаються асимптотами.
або поблизу точок розриву другого
роду, часто трапляється, що графік функції як завгодно близько наближається до
тієї чи іншої прямої. Ці прямі називаються асимптотами.
Для довільних функцій розрізняють вертикальні й похилі, зокрема горизонтальні асимптоти.
Означення
1. Пряма ![]() (1)
називається вертикальною асимптотою графіка функції
(1)
називається вертикальною асимптотою графіка функції ![]() якщо
хоча б одна з границь нескінченна, тобто
якщо
хоча б одна з границь нескінченна, тобто
![]() або
або ![]() (2)
(2)
Вертикальні асимптоти треба шукати в точках розриву другого роду або на скінченій границі області визначення функції D(у). Якщо функція визначена на всій числовій осі і має лише точки розриву першого роду, то її графік вертикальних асимптот не має.
Означення
2. Пряма ![]() (3)
називається похилою асимптотою графіка функції
(3)
називається похилою асимптотою графіка функції ![]() при
при
![]() , якщо
, якщо
![]() (4)
(4)
Звідси випливає теорема:
Теорема. Для того, щоб пряма ![]() була похилою асимптотою
графіка функції
була похилою асимптотою
графіка функції ![]() при
при ![]() , необхідно і достатньо, щоб існували
границі
, необхідно і достатньо, щоб існували
границі
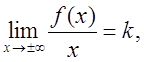
![]() (5)
(5)
Зауваження. Якщо границя ![]() , то асимптоту
, то асимптоту ![]() називають горизонтальною. Якщо і
границя
називають горизонтальною. Якщо і
границя ![]() , то асимптотою графіка функції
, то асимптотою графіка функції ![]() при
при ![]() або
при
або
при ![]() є вісь абсціс ох з рівнянням
є вісь абсціс ох з рівнянням ![]() .
.
Приклад
1. Знайти асимптоти графіка функції 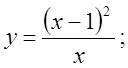
Розв’язання.
Графік має вертикальну асимптоту – вісь оу, яка має рівняння х=0. Для знаходження похилої асимптоти маємо:
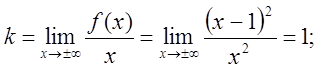
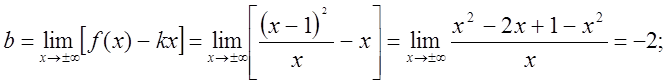
тобто у = х-2 - похила асимптота.
Приклад 2. Знайти асимптоти графіка функції ![]()
Область визначення функції D(х): ![]() , тобто вертикальних
асимптот немає. Для знаходження похилих асимптот маємо:
, тобто вертикальних
асимптот немає. Для знаходження похилих асимптот маємо:
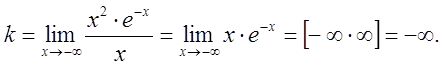
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.