е) 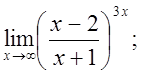 ж)
ж) 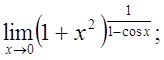
6. а) 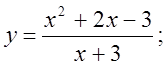 б)
б) 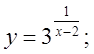 в)
в)
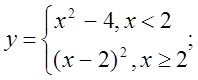
Варіант 11.
1. 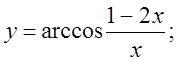 2.
2. ![]() 3.
3.
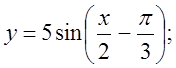
4. а) 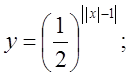 б)
б) 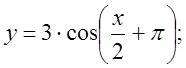 в)
в) 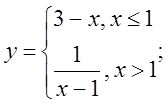
5. а) 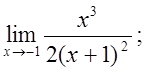 б)
б) 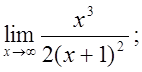 в)
в) 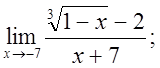
г) 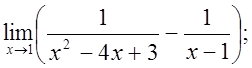 д)
д) 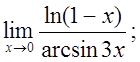
е) 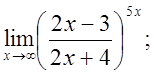 ж)
ж)
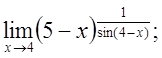
6. а) 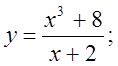 б)
б) 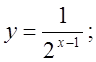 в)
в) 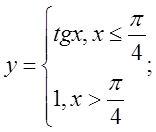
Варіант 12.
1. 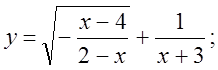 2.
2. ![]() 3.
3. ![]()
4. а) 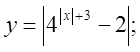 б)
б) 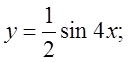 в)
в) 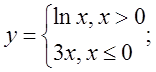
5. а) 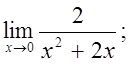 б)
б) 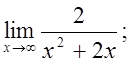 в)
в) 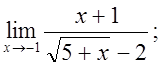
г) 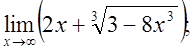 д)
д) 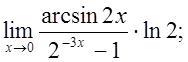
е) 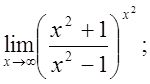 ж)
ж) 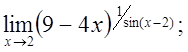
6. а) 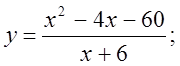 б)
б) 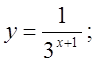 в)
в) 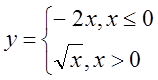
Варіант 13.
1. 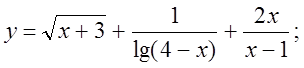 2.
2. 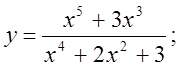 3.
3.
![]()
4. а) ![]() б)
б) ![]() в)
в) 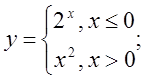
5. а) 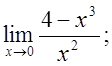 б)
б) 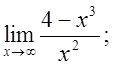 в)
в) 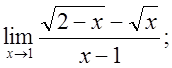
г) 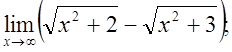 д)
д) 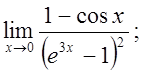
е) 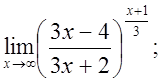 ж)
ж) 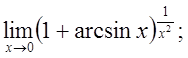
6. а) 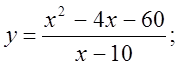 б)
б) 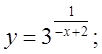 в)
в) 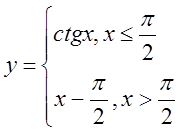
Варіант 14.
1. 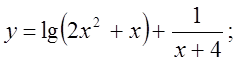 2.
2. 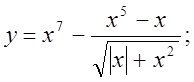 3.
3.
![]()
4. а) 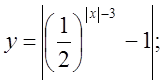 б)
б) ![]() в)
в) 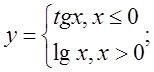
5. а) 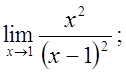 б)
б) 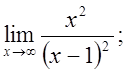 в)
в) 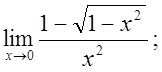
г) 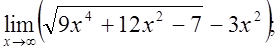 д)
д) 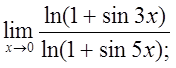
е) 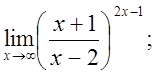 ж)
ж) 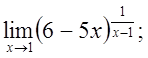
6. а) 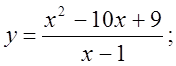 б)
б) 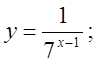 в)
в) 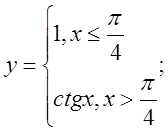
Варіант 15.
1. 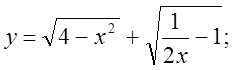 2.
2. 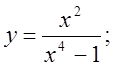 3.
3. 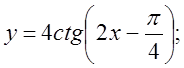
4. а) 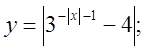 б)
б) 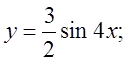 в)
в) 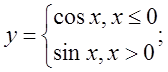
5. а) 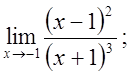 б)
б) 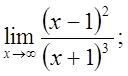 в)
в) 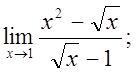
г) 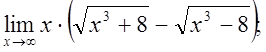 д)
д) 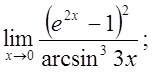
е) 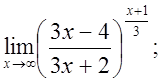 ж)
ж)
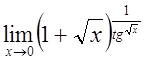
6. а) 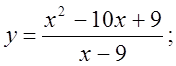 б)
б) 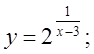 в)
в) 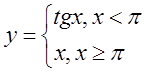
Варіант 16.
1. 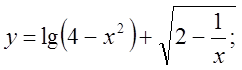 2.
2. 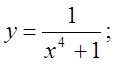 3.
3. 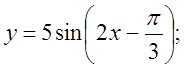
4. а) 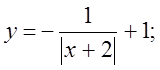 б)
б) ![]() в)
в) 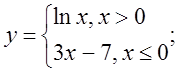
5. а) 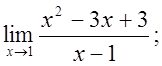 б)
б) 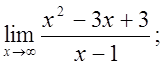 в)
в) 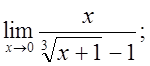
г) 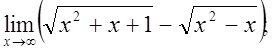 д)
д) 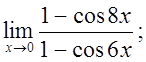
е) 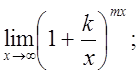 ж)
ж)
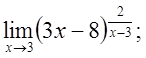
6. а) 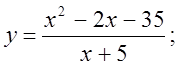 б)
б) 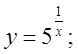 в)
в) 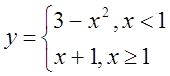
Варіант 17.
1. 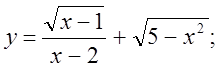 2.
2. 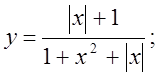 3.
3. ![]()
4. а) 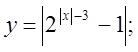 б)
б) ![]() в)
в) 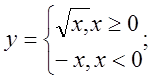
5. а) 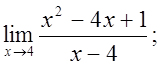 б)
б) 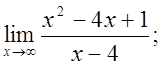 в)
в)
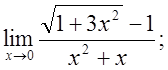
г) 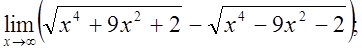 д)
д) 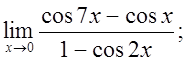
е) 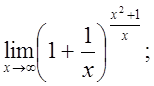 ж)
ж) 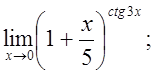
6. а) 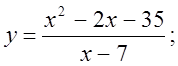 б)
б) 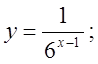 в)
в) 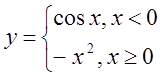
Варіант 18.
1. 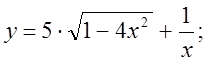 2.
2. ![]() 3.
3. ![]()
4. а) 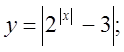 б)
б) 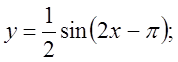 в)
в) 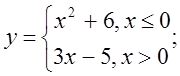
5. а) 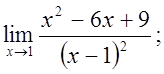 б)
б) 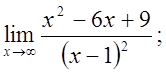 в)
в)
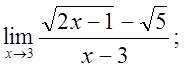
г) ![]() д)
д) 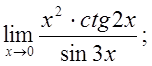
е) 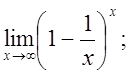 ж)
ж) 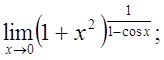
6. а) 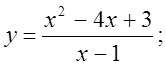 б)
б) 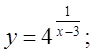 в)
в) 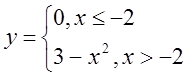
Варіант 19.
1. ![]() 2.
2. ![]() 3.
3. 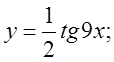
4. а) 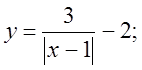 б)
б) 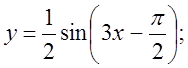 в)
в) 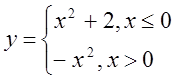
5.а) 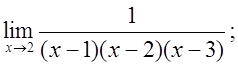 б)
б) 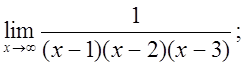
в) 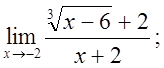
г) ![]() д)
д) 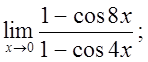
е) 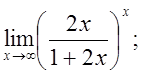 ж)
ж) 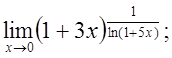
6. а) 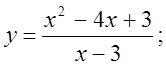 б)
б) 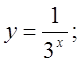 в)
в) 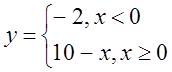
Варіант 20.
1. ![]() 2.
2. ![]() 3.
3.
![]()
4. а) ![]() б)
б) 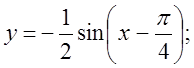 в)
в) 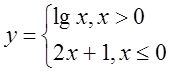
5. а) 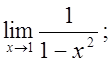 б)
б) 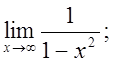 в)
в) 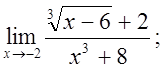
г) ![]() д)
д) 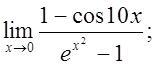
е) 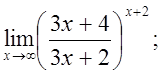 ж)
ж) 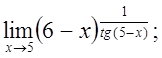
6. а) 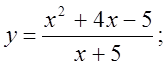 б)
б) 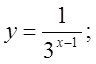 в)
в) 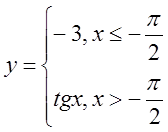
Варіант 21.
1. 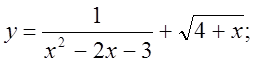 2.
2. 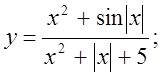 3.
3.
![]()
4. а) 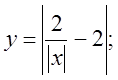 б)
б) ![]() в)
в) 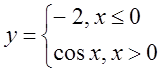
5. а) 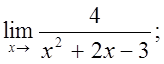 б)
б) 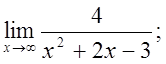 в)
в)
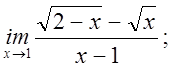
г) ![]() д)
д) 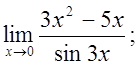
е) 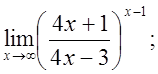 ж)
ж) 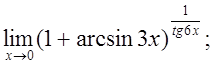
6. а) 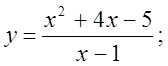 б)
б) 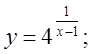 в)
в) 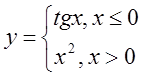
Варіант 22.
1. ![]() 2.
2. 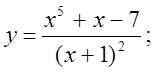 3.
3.
![]()
4. а) ![]() б)
б) 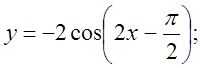 в)
в)
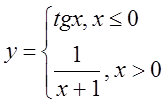
5. а) 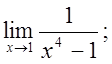 б)
б) 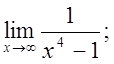 в)
в) 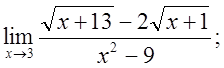
г) 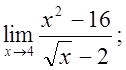 д)
д) 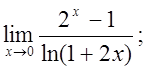
е) 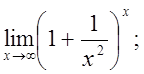 ж)
ж) 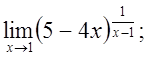
6. а) 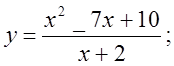 б)
б) 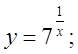 в)
в) 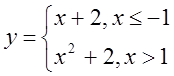
Варіант 23.
1. ![]() 2.
2. 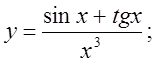 3.
3.
![]()
4. а) 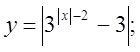 б)
б) 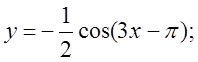 в)
в) 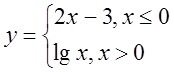
5. а) 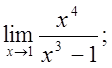 б)
б) 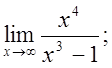 в)
в) 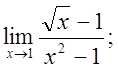
г) ![]() д)
д) 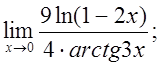
е) 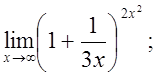 ж)
ж) 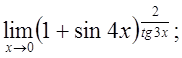
6. а) 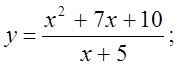 б)
б) 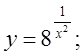 в)
в) 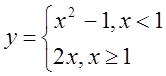
Варіант 24.
1. ![]() 2.
2. ![]() 3.
3. ![]()
4. а) ![]() б)
б) 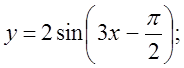 в)
в)
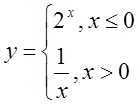
5. а) 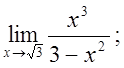 б)
б) 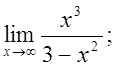 в)
в) 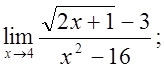
г) ![]() д)
д) 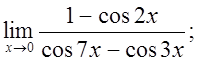
е) 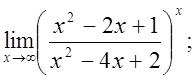 ж)
ж) 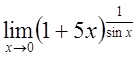
6. а) 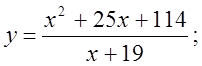 б)
б) 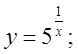 в)
в) 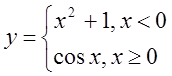
Варіант 25.
1. 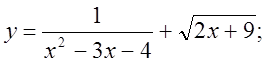 2.
2. ![]() 3.
3.
![]()
4. а) 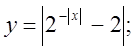 б)
б) ![]() в)
в) 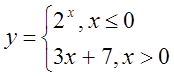
5. а) 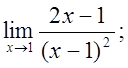 б)
б) 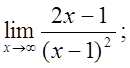 в)
в) 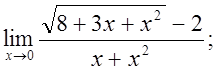
г) 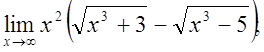 д)
д) 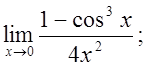
е) 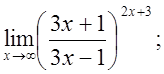 ж)
ж) 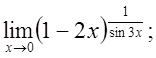
6. а) 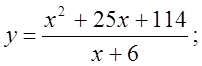 б)
б) 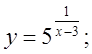 в)
в) 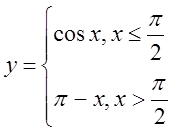
2.1 Загальні поняття та означення. Таблиця похідних
Означення 1. Похідною функцією y=f(x) в точці х називається границя (якщо вона існує) відношення приросту функції
Dy=f(x+Dx)-f(x)
до приросту аргументу Dx, коли приріст аргументу прямує до нуля, тобто
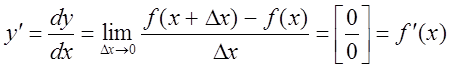 (1)
(1)
Означення 2. Функція, яка має скінчену похідну в точці х, називається диференційовною в цій точці.
Приклад. Знайти похідну функції f(x)=x3 в довільній точці х за означенням.
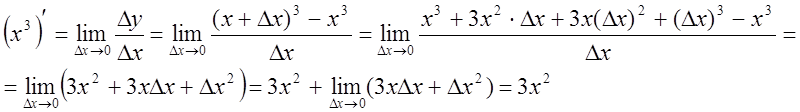
Так можна одержати похідну від усіх основних елементарних функцій і записати їх в таблицю.
1. ![]()
![]()
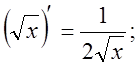
2. 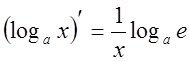
![]()
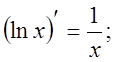
3. ![]()
![]()
![]()
4. ![]()
![]()
5. ![]()
![]()
6. 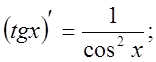
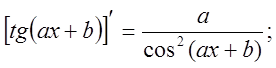
7. 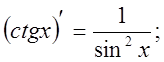
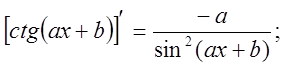
8. 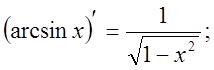
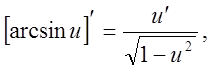 де
де
![]()
9. 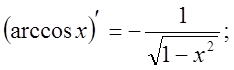
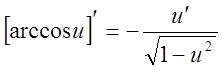
10. 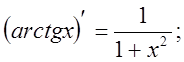
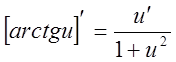
11. 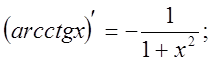
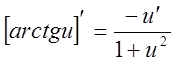
Знаходження похідної називають диференціюванням функції.
2.2 Правила диференціювання
1. ![]() де
де ![]()
2. ![]() , де u(x) і v(x)- диференційовані
функції
, де u(x) і v(x)- диференційовані
функції
3. ![]() ,
,
![]()
4. 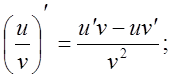
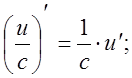
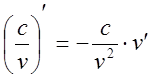
5. ![]()
![]()
Це правило називають правилом диференційовання складної функції:
Похідна складної функції дорівнює добутку похідних зовнішньої і внутрішньої функції.
Виходячи з цього, можна переписати таблицю похідних:
![]()
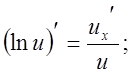
![]() т.
ін.
т.
ін.
6. Якщо функція у(х) подана неявно рівнянням
![]() (1),
(1), ![]() знаходиться
почленним диференціюванням рівняння (1).
знаходиться
почленним диференціюванням рівняння (1).
Приклади.
1) Знайти ![]() , якщо
, якщо ![]()
![]()
2) Знайти ![]() ,
якщо
,
якщо ![]()
Розв’язання
Візьмемо похідну в лівої і правої частини рівняння.
Дістанемо ![]()
![]()
![]()
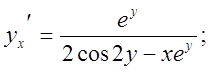
Аналогічно знаходиться похідна функція х(у) поданої неявно:
![]()
![]()
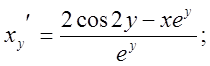
Тобто маємо 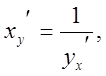 або
або
Похідні
прямої та оберненої функції зв’язані співвідношенням ![]() .
.
7. Якщо функція у(х) подана параметрично рівняннями ![]()
![]() то
то
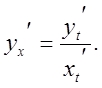
Аналогічно знаходиться 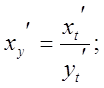
Приклад. 3)
Знайти ![]() якщо
якщо 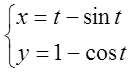
Розв’язання.
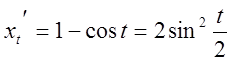
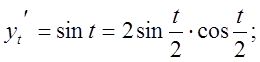
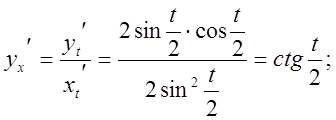
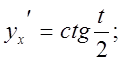
8. Логарифмічне диференціювання.
Це є так званий штучний прийом диференціювання показниково – степеневої функції y=uv, де и=и(х)>0, v=v(x)- диференційовні функції.
По-перше, за правилом логарифмування показникової функції маємо:
![]()
По-друге, за правилом диференціювання складної функції маємо:
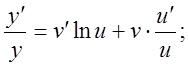
Таким чином, остаточно маємо
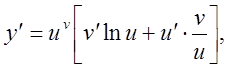 або
або
![]()
Тобто, похідна показниково – степеневої функції дорівнює сумі двох додатків, перший з яких є похідна показникової функції, другий – похідна степеневої функції.
Зауваження Цей прийом можна застосовувати для знаходження похідної від громіздких добутків, частків, степенів і тощо.
Приклади
4) Знайти ![]() якщо
якщо 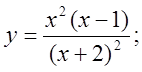
Розв’язання.
Прологарифмуємо функцію:
![]()
Знайдемо похідну від лівої та правої частини
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.