Теоретичний матеріал та контрольні завдання зі зразками вирішення з вищої математики
Для студентів заочної форми навчання за фахом
7.090202 „Технологія машинобудування”
7.090216”Гірниче обладнання”
7.090218 „Металургійне обладнання
1. Вступ до аналізу
Математичний аналіз вивчає змінні величини – функцію, теорію границь, диференціальне та інтегральне числення.
a. Загальні поняття та означення
Означення 1. Множина – це сукупність деяких об’єктів (елементів множини), виділених за певною ознакою з інших об’єктів.
Факт належності елемента а множини А позначається:
а ![]() А
А
Основні числові множини:
N - натуральні числа,
Z - цілі числа,
Q - раціональні числа,
R - дійсні числа,
С - комплексні числа.
Має місто співвідношення:
N cZcQcRcC
Наприклад.Множина
раціональних чисел Q утворена всіма дробами вигляду m/n,
де m![]() Z,
n
Z,
n![]() N.
N.
Тобто, довільне раціональне число зображається скінченним або нескінченним періодичним десятковим дробом.
Означення 2. Числа, які зображаються нескінченним неперіодичним десятковим дробом, називають ірраціональними.
Наприклад. π ≈ 3,1415926536, e ≈ 2,71828181
![]() ≈ 1,414213562343
≈ 1,414213562343
Довільне ірраціональне число можна з довільною точністю наблизити раціональним числом.
Наприклад. З точністю до ∆ = 0,01:
π ≈ 3,14; e ≈ 2,72; ![]() ≈ 1,41.
≈ 1,41.
Раціональні та ірраціональні числа утворюють множину дійсних чисел R.
Відрізняють такі підмножини дійсних чисел:
інтервал ( відкритий проміжок) – (а, в) або а < х < в;
відрізок - [а, в] або а ≤ х ≤ в;
напівінтервал - [а, в) або (а, в];
нескінченні інтервали – (-∞, в) або (а, ∞), (-∞,∞) = R вся множина дійсних чисел.
Означення 3. Модулем або абсолютною величиною дійсного числа х називається вираз:
│х│= х, якщо х ≥ 0, та │х│= - х, якщо х < 0.
Властивості модуля числа:
1. │х│≥ 0;
2. х ≤ │х│;
3. │х + у│≤ │х│+ │у│;
4. │х × у│≤ │х│× │у│, де х, у – є R;
5. │х│< а рівносильно -а < х < а, х є (-а, а);
6. │х - а│< б <=> а – б < х < а + б, х є (а – б, а + б).
Означення 4. Інтервал (а – б, а + б) називається б-колом точки а.
Множина комплексних чисел С утворена приєднанням до множини дійсних чисел R числа і, для якого і2 = -1, а також всіх чисел вигляду а + в × і, де а, в є R.
Означення 5. Комплексними називаються числа вигляду Z = a
+ i×в, де і =![]() , а і в – дійсні
числа, які позначаються а = ReZ, в = ImZ і називаються відповідно дійсною і уявною частинами комплексного
числа Z є С.
, а і в – дійсні
числа, які позначаються а = ReZ, в = ImZ і називаються відповідно дійсною і уявною частинами комплексного
числа Z є С.
Окрім стандартної форми запису комплексного числа Z = a + ві, використовується тригонометрична форма запису:
Z = r × (cosφ + іsinφ),
де: r = │ Z │= √а2 + в2, φ = argZ = arctgb/a.
Ясно, що кут φ = argZ – визначений однозначно, якщо накласти додаткову умову о ≤ φ ≤ 2 π.
1.2 Функція та її властивості. Класифікація функцій
Величину, яка може приймати різні числові значення, називають змінною.
Означення 1. Якщо кожному значенню змінної х є D за деяким законом ƒ (по деякому правилу ƒ) ставиться у відповідність одне і тільки одне значення другої змінної у є Е, тоді у = ƒ(х) є функція з областю визначення D(х) і множиною значень Е(у).
При цьому вживаються терміни:
х– незалежна змінна (аргумент),
у– залежна змінна (функція).
Функцію можна задати аналітично (формулою), графічно, таблицею, програмою для ЕОМ.
Означення 2. Графіком функції у = ƒ(х) називають геометричне місце точок М(х, ƒ(х)) площини ОХУ, абсциси яких належать D(х), а ординати – Е(у).
Як правило, графік функції – це лінія (крива) площини ОХУ.
Означення 3. Функція у = ƒ(х) визначена в інтервалі, симетричному відносно нуля, називається:
а) парною, якщо ƒ(-х) = ƒ(х) ,
б) непарною, якщо ƒ(-х) = -ƒ(х).
Зрозуміло, що графік парної функції симетричний відносно осі ординат ОУ, а графік непарної – відносно початку координат (0,0).
Приклад 1. Побудувати графік функції
у = х2 - 2│х│
Розв’язання:
1). За означенням:│х│= х, якщо х ≥ 0, та │х│= - х, якщо х < 0.
Таким чином, у = х2 – 2х, х ≥ 0,
у = х2 + 2х, х < 0.
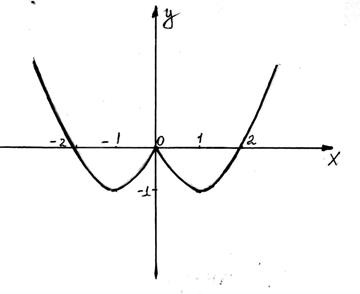 |
Рисунок 1
Дійсно, функція у = х2 – 2│х│- парна, тобто вона має бути симетрична відносно осі ординат ОУ (див.рис. 1)
Означення 4. Якщо правило ƒ – взаємно однозначна відповідність між множинами D(х) і Е(у), тоді існує єдина функція ƒ-1 ≡ d, яка задовольняє умові:
ƒ(d(у)) = у, d(ƒ(х)) = х
для всіх х є D(у) ≡ Е(х), у є Е(у) ≡ D(х).
Ця функція х = ƒ-1(у) називається оберненою для функції ƒ(х).
Приклад 2. Знайти функцію, обернену до даної функції:
х = азу – 2
Розв’язання:
Маємо азу = х + 2. Логарифмуючи обидві частини рівності, одержимо:
3уlogаа = logа(x + 2)
Враховуючи, що logaa = 1, маємо:
у = ⅓loga(х + 2)
Означення 5. Функція ![]() , яка визначена на
всій числовій осі, називається періодичною, якщо існує таке число а ¹ 0, що для всіх х виконується умова:
, яка визначена на
всій числовій осі, називається періодичною, якщо існує таке число а ¹ 0, що для всіх х виконується умова: ![]() .
.
Найменше додатнє число а, яке задовольняє такій умові, називають періодом функції і позначають Т. Розглянемо класифікацію функцій.
Означення 6. Основними єлементарними функціями є:
1)
степенева - ![]() ,
, ![]()
2)
показникова - ![]() , а > 0, а ¹
1.
, а > 0, а ¹
1.
3)
Логарифмічна - ![]() , а > 0, а ¹
1.
, а > 0, а ¹
1.
4)
Тригонометричні - ![]()
5)
Обернені тригонометричні -![]() .
.
Означення 7. Якщо ![]() , а
, а ![]() , то функція
, то функція ![]() називається
складеною або суперпозицією (композицією) функцій
називається
складеною або суперпозицією (композицією) функцій ![]() і
і
![]() .
.
Означення 8. Елементарними функціями називають або основні елементарні, або ті, які утворено з них за допомогою скінченного числа арифметичних дій чи скінченного числа суперпозицій функцій.
В математиці широко використовують алгебраїчні елементарні функції
а) многочлен (поліном), або ціла раціональна функція
![]() ,
,
де ![]() - степень многочлена, а0,
а1, ..., аn – дійсні коефіціенти (сталі числа)
- степень многочлена, а0,
а1, ..., аn – дійсні коефіціенти (сталі числа)
б) дробово – раціональна функція (відношення двох многочленів):
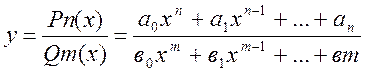
Прикладом дробово-раціональної функції є дробово-лінійна:
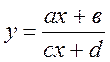 ,
,
а також 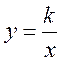 (гіпербола), де
(гіпербола), де ![]() .
.
Зауваження.
1.
Рівнянням ![]() неявно подається функція у(х),
або х(у), наприклад: х2 + у2 = 0.
неявно подається функція у(х),
або х(у), наприклад: х2 + у2 = 0.
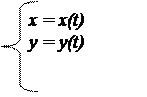 |
2. Рівняннями параметрично подається функція у(х),
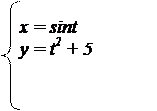 |
або х(у), наприклад
3). Графік функції у = Аf[k(x-a)]+B можна побудувати за допомогою деформації і паралельного зсуву графіка у = f(x).
Це можна зробити в такій послідовності:
а) у = f(x);
б) у = f(x-а) зміщення по осі ОХ графіка у = f(x) на величину а;
в) у = f[k(x-a)] – розтяг уздовж осі ОХ в ![]() разів
графіка у = ƒ(х - а);
разів
графіка у = ƒ(х - а);
г) у = Аf[k(x-a)] – розтяг уздовж осі ОУ в А разів графіка у = f[k(x-a)];
д) у = Аf[k(x-a)] + В зміщення по осі ОУ графіка ![]() на величину В.
на величину В.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.