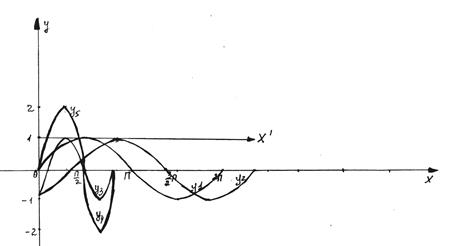
Приклад 3. Побудувати графік функції:
у = 2sin3(x
- ![]() - 1
- 1
Це можна зробити в такій послідовності:
а) у1 = sinx;
б) у2 = sin(x
- ![]() - графік функції у = sinx змістився по осі ОХ на величину
- графік функції у = sinx змістився по осі ОХ на величину ![]() вправо;
вправо;
в) у3 = sin3(x - ![]() , графік функції у = sin(x
-
, графік функції у = sin(x
- ![]() розтягнувся уздовж осі ОХ в
розтягнувся уздовж осі ОХ в ![]() разів (в даному випадку
графік у = sin(x -
разів (в даному випадку
графік у = sin(x - ![]() сжався
по осі ОХ);
сжався
по осі ОХ);
г) у4 = 2sin3(x
- ![]() , графік функції у = 2sin3(x
-
, графік функції у = 2sin3(x
- ![]() , розтягнувся в 2 рази вздовж осі ОУ;
, розтягнувся в 2 рази вздовж осі ОУ;
д) у5 = 2sin3(x
- ![]() -1; графік функції у = 2sin3(x
-
-1; графік функції у = 2sin3(x
- ![]() змістився по осі ОУ на одну одиницю вниз , або
вісь ОХ підняли на одну одиницю угору по осі ОУ. Графік заданої
функції дивіться на рисунку 2:
змістився по осі ОУ на одну одиницю вниз , або
вісь ОХ підняли на одну одиницю угору по осі ОУ. Графік заданої
функції дивіться на рисунку 2:
 |
|||
|
|||
4). Графік функції у = | f(x) | одержують дзеркальним відображенням від осі ОХ від’ємної частини графіка у = f(x). Графік функції у = f( |х-а| ) одержують дзеркальним відображенням від прямої х = а частини графіка функції у = f(х-а), що побудована при х > а.
Тобто, в цьому разі графік функції у = f( |х-а| ) симетричний відносно прямої х = а
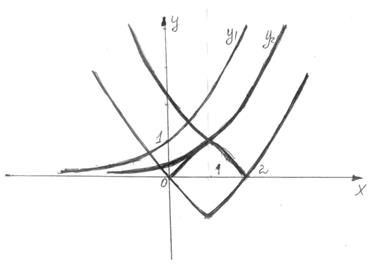
Приклад 4. Побудувати графік функції:
у = |2|х-1 | - 2|
Це можна зробити в такій послідовності:
а) у = 2х;
б) у = 2х-1 графік функції у = 2х змістився вздовж осі ОХ;
в) у = 2|х-1| графік одержують дзеркальним відображенням від прямої х = 1 частини графіка функції у = 2х-1, що побудована при х > 1;
г) у = 2|х-1| - 2 цей графік одержують зміщенням графіка функції у = 2|х-1| вздовж осі ОУ на дві одиниці вниз;
д) у = |2|х-1 | - 2| цей графік одержують дзеркальним відображенням від осі ОХ від’ємної частини графіка у = 2|х-1| - 2.
Графік заданої функції дивіться на рисунку 3:
 |
1.3 Елементи теорії границь. Нескінчено великі та
нескінчено малі величини та їх властивості
Поняття границі функції – одне з найважливіших у вищій математиці.
Означення 1. Якщо кожному натуральному числу n є N поставлено у відповідність деяке дійсне число хn, то кажуть, що задана послідовність х1, х2, ... хn, ... тобто {хn}.
Означення 2. Послідовність {хn} називається збіжною, якщо для будь-якого числа ε > 0 можна знайти такий номер N = N(ε), що при всіх n > N виконується нерівність:
|хn-a| < ε,
де число а називається границею послідовності {хn}, при цьому вживається запис:
![]() хn = а
(1)
хn = а
(1)
Теорема (Вейєрштрасса): Зростаюча послідовність
х(n) = (1+ ![]() )n обмежена зверху і збігається до деякого числа, яке Ейлер позначив буквою e, тобто:
)n обмежена зверху і збігається до деякого числа, яке Ейлер позначив буквою e, тобто:
![]() (1 +
(1 + ![]() )n =
e ≈ 2,7182818 (2)
)n =
e ≈ 2,7182818 (2)
Означення 3. Число А називається границею функції f(x)при х →х0 (або в точці х0), якщо для будь-якого ε > 0 можна знайти таке число δ = δ(ε) > 0, що при всіх х, які задовольняють нерівність:
|х – х0| < δ
виконується нерівність | f(x) - А| < ε, тобто:
![]() f(x) = А
(3)
f(x) = А
(3)
(або f(x) → А при х → х0)
Символічно: ![]() ε > 0
ε > 0 ![]() δ > 0
δ > 0 ![]() х
х
![]() х, |х – х0| < δ; | f(x) - А| < ε.
х, |х – х0| < δ; | f(x) - А| < ε.
Означення 4. Число А називається правою (лівою) границею функції f(x), в точці х0, якщо для будь-якого ε > 0 знайдеться таке число δ = δ(ε) > 0, що при всіх х, які задовольняють нерівності:
0 < х – х0 < δ
(0 < х0 – х < δ), виконується нерівність:
| f(x) - А| < ε, тобто:
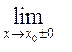 f(x) = f(x0
f(x) = f(x0 ![]() 0) = А (4)
0) = А (4)
Нехай функція f(x) визначена при х > х0 (х < х0).
Означення 5. Число А
називається границею функції f(x)
при х → ![]() (х → -
(х → -![]() ), якщо для будь-якого ε > 0 можна знайти
таке число N = N(ε), що при всіх х, які задовольняють нерівність:
), якщо для будь-якого ε > 0 можна знайти
таке число N = N(ε), що при всіх х, які задовольняють нерівність:
|х| > N
виконується нерівність
| f(x) - А| < ε, тобто
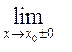 f(x) = А
(5)
f(x) = А
(5)
(або f(x) → А, х→+∞; f(x) → А, х→-∞ )
Означеня 6. Функція f(x) називається нескінченно великою в точці х0, якщо для будь-якого М > 0 можна знайти таке δ > 0, що при всіх х, які задовольняють нерівність |х – х0| < δ
Виконується нерівність | f(x) | > М; тобто:
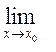 f(x) =
f(x) = ![]()
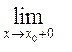 f(x) =
f(x) = ![]()
Означення 7. Функція f(x)
називається нескінченно малою при х → х0 (або в точці х0), якщо 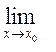 f(x) = 0
f(x) = 0
Теорема 1. Для того, щоб функція f(x) мала в точці х0 границею число А, необхідно й достатньо, щоб в околі точки х0 виконувалось співвідношення
f(x) = А + ![]() (х),
(х),
де - ![]() (х) – нескінченно мала в
точці х0.
(х) – нескінченно мала в
точці х0.
Теорема 2. Сума (різниця), добуток нескінченно малих є нескінченно мала.
Теорема 3. Добуток нескінченно малої функції на обмежену функцію є нескінченно мала.
Теорема 4. Якщо ![]() (х) –
нескінченно мала в точці х0, то функція f(x) =
(х) –
нескінченно мала в точці х0, то функція f(x) = 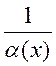 є нескінченно велика в цій точці і навпаки.
є нескінченно велика в цій точці і навпаки.
1.4 Властивості границь. Важливі границі та їх застосування
Розглянемо основні теореми про властивості границі функції.
Теорема. Якщо функції f(x) і φ(x) мають границі в точці х0:
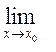 f(x) = А,
f(x) = А, 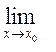
![]() (x) = В,
(x) = В,
то функції [f(x)± φ(x) ]; f(x) ![]() φ(x);
φ(x); 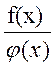 (при В ≠ 0) також мають границі в точці х0,
при чому:
(при В ≠ 0) також мають границі в точці х0,
при чому:
1). 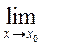 [f(x) ± φ(x) ]= А ± В
[f(x) ± φ(x) ]= А ± В
2). 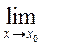 [f(x)
[f(x) ![]() φ(x) ]= А
φ(x) ]= А ![]() В
В
3). 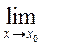
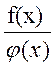 =
=
![]() ( В ≠ 0 )
( В ≠ 0 )
Наслідки:
1). 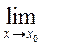 [с
[с![]() f(x)] = с
f(x)] = с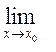 f(x), де с –
довільна стала.
f(x), де с –
довільна стала.
2). 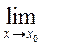 [ f(x)]m = [
[ f(x)]m = [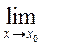 f(x)]m, де m
f(x)]m, де m
![]() N
N
3). Нехай f(x), φ(x), g(x)
– функції, визначені на множині Х, ![]()
![]() Х виконуються нерівності: f(x) ≤ φ(x) ≤ g(x).
Х виконуються нерівності: f(x) ≤ φ(x) ≤ g(x).
Тоді, якщо існують границі 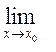 f(x) =
f(x) = 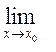 g(x) = А, то існує і
границя функції φ(x) у точці х0,
при чому
g(x) = А, то існує і
границя функції φ(x) у точці х0,
при чому 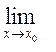 φ (x) = А.
φ (x) = А.
Зауваження. При обчисленні 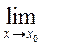 [f(x) - φ(x) ],
[f(x) - φ(x) ], 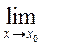
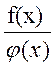 , коли f(x) і φ(x) – нескінчено великі [∞ - ∞,
, коли f(x) і φ(x) – нескінчено великі [∞ - ∞, ![]() ], або коли f(x) і φ(x)– нескінчено малі [
], або коли f(x) і φ(x)– нескінчено малі [![]() , 0×∞] виникають
невизначеності і обчислення границь в цих випадках називається розкриттям
невизначеності.
, 0×∞] виникають
невизначеності і обчислення границь в цих випадках називається розкриттям
невизначеності.
Обчислення границь функцій у багатьох випадках можна проводити за допомогою двох важливих границь:
1. 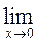
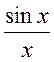 =
[
=
[ ![]() ] = 1;
] = 1;
2. 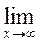 ( 1+
( 1+ ![]() )х
= [1
)х
= [1![]() ] =
] = ![]() ;
;
Часто використовуються також наслідки цих формул:
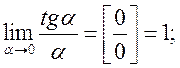
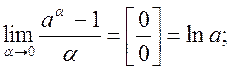
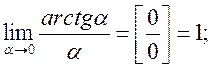
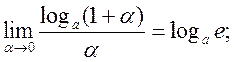
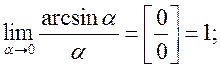
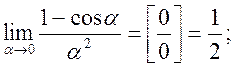
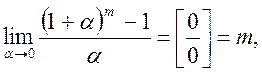
де a = a(х) – нескінченно мала в точці х0.
Приклади на важливі границі:
1. 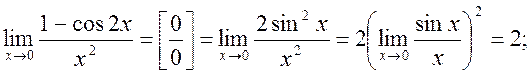
2. 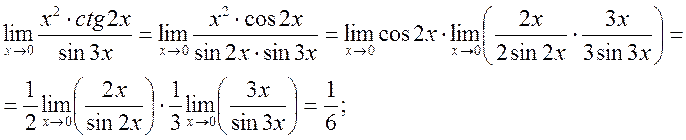
3. 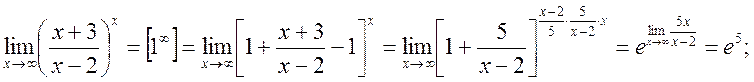
4. 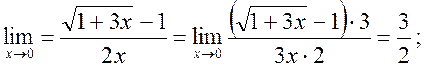
5.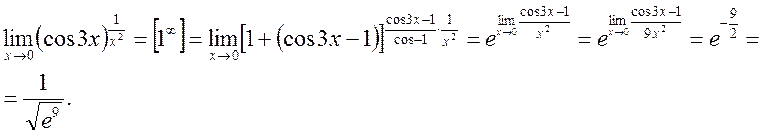
1.5 Порівняння нескінченно малих
та нескінченно великих.
Еквівалентні нескінченно малі
При дослідженні функції часто доводиться мати справу не з однією, а з кількома нескінченно малими функціями в даній точці.
Для їх порівняння вивчають частку цих функцій.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.