причем: А ∙ 1 = 1 А = А; А ∙ 0 = 0; α ∙(β ∙ А) = β ∙(α ∙ А);
(α + β) ∙ А = αА + βА; α ∙ (А ± В) = αА ± αВ.
в) Умножение на матрицу (на скалярную матрицу) возможно в том случае, когда число элементов в строке матрицы А равно числу элементов в столбце матрицы В. (или число столбцов А равно числу строк В).
А ∙ В = С, где сij= ai1 ∙ b1j + ai2 ∙ b2j + … + ain ∙ bnj., (2.1.3)
где размерность матрицы-результата - Аm x n ∙ Bn x k = Cm x k.
Матрица вида D = d ∙ E =  называется скалярной матрицей.
Очевидно, что A ∙ D = A ∙ α ∙ E = α ∙A ∙ E= α ∙ A.
называется скалярной матрицей.
Очевидно, что A ∙ D = A ∙ α ∙ E = α ∙A ∙ E= α ∙ A.
Умножение матриц в большинстве случаев не обладает перестановочным свойством. А ∙ В ≠ В ∙ А.
Если такое возможно (А ∙ В = В ∙ А), то А и В называются перестановочными. Например, нулевая матрица О, единичная Е и скалярная матрица перестановочны относительно любой матрицы.
Свойства умножения:
1) (А ∙ В) ∙ С = А ∙ (В ∙ С);
2) α ∙ (А ∙ В) = (α ∙ А) ∙ В = А ∙(α ∙ В);
3) (А ± В) ∙ С = А ∙С ± В ∙С; (2.1.4)
4) С ∙ (А ± В) = С ∙А ± С ∙В;
5) det (A ∙ B) = det A ∙ det B.
Пример №1 Как должен выглядеть столбец матрицы В, чтобы в результате умножения Аm x n ∙ Bn x 1 = Cm x 1.получить:
а) первый столбец матрицы А ? .
б) сумму третьего и четвёртого элемента каждой строки?
Ответ: а) 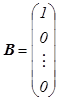 б)
б) 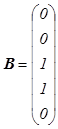 .
.
Пример №2 Пусть B1 x m ∙ Аm x n = C1 x n . На что надо умножать А, чтобы получить последнюю строку матрицы А?
Ответ: ![]() .
.
В среде "MathCad" часть матрицы можно выделить при помощи функции Submatrix (A; k; m; l; n). У этой функции первый аргумент – название матрицы, вторй и третий – начальная и конечная строка, четвёртый и пятый – границы выделяемой части матрицы по столбцам.
г) Возведение в степень.
![]() = А ∙ А ∙ … ∙ А – к раз. (2.1.5)
= А ∙ А ∙ … ∙ А – к раз. (2.1.5)
д) Транспонирование матриц.
Транспонированная матрица АТ – это матрица, у которой строки заменены столбцами соответствующего номера из исходной матрицы. Операция транспонирования верна не только для квадратных матриц.
А = 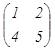 , АТ =
, АТ =  ,
, ![]() ,
ВТ =
,
ВТ = ![]() .
.
Свойства:
1) (АТ)Т = А;
2) (А + В)Т = АТ + ВТ; (2.1.6)
3) (А ∙ В)Т = ВТ ∙ АТ;
4) det AТ = det A, если А – квадратная.
Если АТ = А, то А - называется симметрической.
2.2 Вычисление определителя матрицы.
Определителем квадратной матрицы называется число равное алгебраической сумме n! слагаемых, каждое из которых представляет собой произведение n элементов матрицы, стоящих в разных строках и разных столбцах, взятое со знаком "+", если перестановка индексов элементов четная и "-", если нечетная. Если det A =0, то матрица называется особенной.
Правила практического вычисления определителей (для размерности 4´4 и выше):
а) разложение по строке с номером k
det
A =![]() j=1…n (2.2.1)
j=1…n (2.2.1)
б) разложение по столбцу с номером k.
det
A =![]() i=1…n (2.2.2)
i=1…n (2.2.2)
в) при помощи элементарных преобразований, приводящих его к треугольному виду.
Допустим а11 ≠ 0. Тогда все элементы первого столбца (строки) делим на а11:
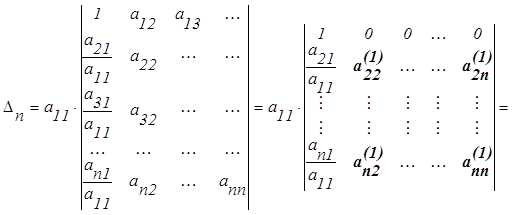
![]() где
где 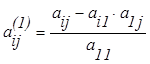 .
.
Этот же прием применяется к ![]() . Последовательно получим
. Последовательно получим ![]() . Если на некотором шаге первый
элемент окажется равен нулю, необходимо поменять местами строки.
. Если на некотором шаге первый
элемент окажется равен нулю, необходимо поменять местами строки.
Например:

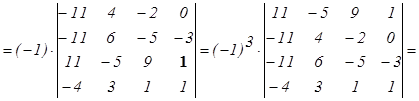
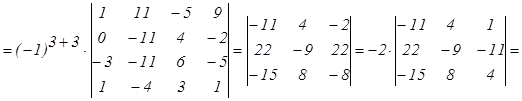
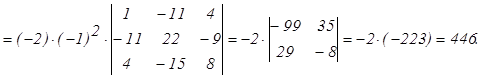
2.3 Нахождение обратной матрицы.
Теорема: Любая неособенная матрица имеет обратную.
Свойства:
1) ![]() .
.
2) (А ∙ В)-1 = В-1 ∙ А-1 (2.3.1)
3) (А-1)Т = (АТ)-1
Доказательство:
1)
Так как А-1
∙ А = Е то det A-1 ∙ det A = det E или ![]() .
.
2) Умножим левую часть на произведение А ∙ В. Получим:
А ∙ В ∙(В-1 ∙ А-1) = А ∙ Е ∙ А-1 = Е, т.е. А ∙ В – есть обратная матрица к В-1 ∙ А-1 или (А ∙ В)-1 = В-1 ∙ А-1.
3) (А-1 ∙ А)Т = АТ ∙ (А-1)Т, т.е. (АТ)-1 = (А-1)Т.
Правила практического вычисления обратной матрицы.
1) При помощи алгебраических дополнений
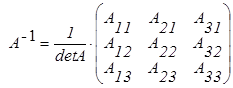 . (2.3.2)
. (2.3.2)
где ![]() - алгебраические дополнения к
элементам матрицы А.
- алгебраические дополнения к
элементам матрицы А.
2) При помощи метода Гаусса.
Составляется матрица: М
= (![]() |
| ![]() ) и элементарными преобразованиями
матрица М приводится к специальному ступенчатому виду, тогда получаем (
) и элементарными преобразованиями
матрица М приводится к специальному ступенчатому виду, тогда получаем (![]() |
| ![]() ). Эту операцию можно произвести
при помощи функции rref (M).
). Эту операцию можно произвести
при помощи функции rref (M).
2.4 Собственные числа матрицы и соответствующие им собственные векторы.
Пусть Аn x n матрица с действительными элементами, тогда матрица (А – λ ∙ Е) n x n называется характеристической матрицей для матрицы А, а det(А – λ ∙ Е) – есть характеристический многочлен ( n – ой степени от λ ), а его корни λі – собственными числами матрицы А.
Каждому собственному
числу соответствует собственный вектор матрицы А: ![]()
Теорема. (Тождество Гамильтона-Келли). Всякая квадратная матрица А является корнем своего характеристического полинома.
det(А – λ ∙ Е)=0 (2.4.1)
В среде «MathСad» заданы следующие встроенные функции:
еigenvals (M) - возвращает вектор, элементами которого являются собственные числа матрицы М.
еigenvecs (M) – возвращает матрицу, состоящую из нормализованных собственных векторов матрицы М, соответствующих собственным числам матрицы М. Причём в n-ном столбце матрицы возвращается собственный вектор, соответствующий n-ному собственному числу, возвращаемому функциейeigenvals.
eigenvec (M,z) – возвращает нормализованный собственный вектор матрицы М, соответствующий собственному числу zматрицы М. Собственное число zможет быть комплексным.
2.5 Норма матрицы.
Норма матрицы
обозначается![]() . Это действительное число, удовлетворяющее условиям:
. Это действительное число, удовлетворяющее условиям:
1) ![]() > 0, причем
> 0, причем ![]() = 0 тогда и только тогда, когда А
= 0.
= 0 тогда и только тогда, когда А
= 0.
2) ![]() (в частности,
(в частности, ![]() )
)
3) ![]() .
(2.5.1)
.
(2.5.1)
4) ![]() .
.
Норма матрицы называется канонической, если выполняются еще два свойства:
5) ![]() .
(2.5.2)
.
(2.5.2)
6) Из неравенства ![]() следует
следует ![]()
Норма матрицы согласуется
с нормой вектора в данном пространстве. Итак, если для ![]() введена
норма
введена
норма ![]() , то для матрицы
, то для матрицы
 . (2.5.3)
. (2.5.3)
Рассмотрим наиболее распространенные согласованные нормы:
Норма вектора Норма матрицы
![]()
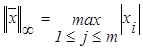
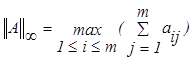 (2.5.4)
(2.5.4)
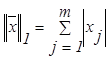
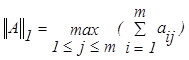 (2.5.5)
(2.5.5)
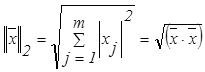
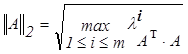 , (2.5.6)
, (2.5.6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.