Математика \ Высшая математика

Элементы теории погрешностей. Матрицы. Точные и итерационные методы решения систем линейных уравнений. Нахождение собственных векторов и собственных чисел матриц, страница 4

Если , то система имеет единственное решение и данный итерационный процесс (4.1.2) сходится к решению со скоростью геометрической прогрессии.

Доказательство: Для всякого решения системы (4.1.1) имеем следовательно или 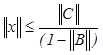. Рассмотрим - решение системы, тогда - погрешность при решении. Тогда , (т.к. и ) а значит следовательно или . Таким образом . Что и требовалось доказать.

Качество итерационного процесса удобно характеризовать величиной

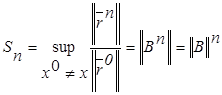(4.1.4)

Можно гарантировать, что , если .

Замечание Собственные числа матрицы . Если условие теоремы выполнено для некоторой нормы, то её утверждение справедливо для любой эквивалентной ей нормы. В частности, процесс итераций заведомо сходится, если , где п – число неизвестных в системе.

4.2 Оценка погрешности приближений процесса итераций

Пусть x⁽^k^-1) и x⁽^k⁾ – два последовательных приближения решения линейной системы (4.1.1).

Тогда при р ≥ 1 имеем:

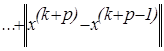(4.2.1)

Так как итерационный процесс задан по схеме (4.1.2), то

и следовательно

(4.2.2)

подставим (4.2.2) в (4.2.1)

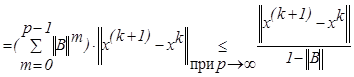
Итак 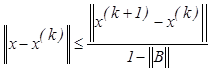или 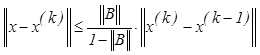. Если , то

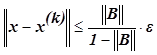(4.1.5)

Однако на практике быструю оценку достаточной точности можно получить при взгляде на соседние итерации. Если они приближенно равны, то стоит проверить оценку погрешности.

Рассмотрим один из способов получения матриц В и С. При a_ij ≠ 0

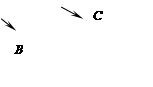
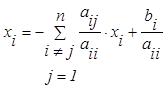
, (4.1.6)

Тогда при наличии в матрице А диагонального преобладания выполняется условие сходимости метода простой итерации, так как если

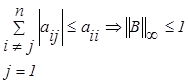. (4.1.7)

Пример: Решить систему методом простой итерации.

4 x₁ + 0,24 x₂ – 0,08 x₃ = 8;

0,09 x₁ + 3 x₂ – 0,15 x₃ = 9;

0,04 x₁ – 0,08 x₂ + 4 x₃ = 20.

Решение:Преобразуем систему уравнений:

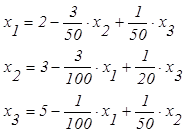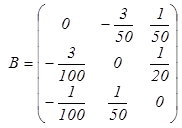тогда и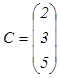

За начальное приближение выбираем x⁽⁰⁾ : = С и выполняем вычисления по итерационной схеме x⁽^k⁾ : = C + (B ∙ x⁽^k^-¹⁾)

Таблица 1 – Вычисления по методу простой итерации

		Итерации
		0	1	2	3	4
*Приближения решения*	х₁	2	1,92	1,909	1,909	1,909
	х₂	3	3,19	3,194	3,195	3,195
	х₃	5	5,04	5,045	5,045	5,045

Как видно из таблицы 1, уже четвертая итерация дает тот же результат, что и третья. Относительная погрешность вычислений - 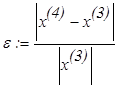= 5.577 х 10 ^-6.

4.3 Метод Зейделя.

Пусть решается система уравнений, все диагональные элементы которой – ненулевые. В итерационном методе Зейделя последовательно уточняются компоненты решений, причем k-ая компонента находится из k-го уравнения.

Именно, если , то следовательно приближение определяется из системы отношений:

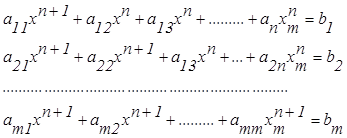
в матричной форме:

или где

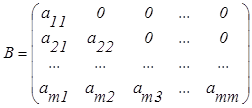и .

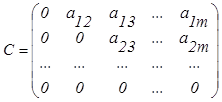Метод Зейделя эквивалентен методу простой итерации, поэтому для его сходимости необходимо, чтобы все собственные числа матрицы – В^-1 ∙ С были по модулю меньше единицы. Или иначе

Теорема (Необходимое и достаточное условие сходимости метода Зейделя) Все корни уравнения по модулю меньше 1.

Таким образом, метод Зейделя эквивалентен некоторому методу простой итерации, поэтому для его сходимости необходимо, и достаточно, чтобы все собственные числа матрицы - В^-1 ∙ С по модулю были меньше единицы.

Из равенства видно, что собственные числа матрицы (- В^-1 ∙ С) будут корнями уравнения .

Обычно метод Зейделя сходится быстрее метода простой итерации

Пример: Решим ту же задачу методом Зейделя.

; ;

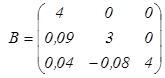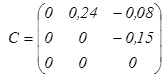Находим последовательно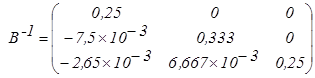

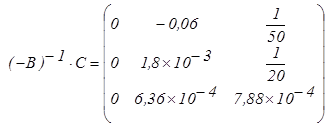
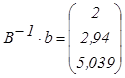
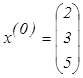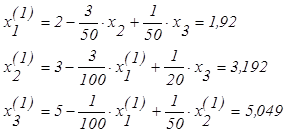
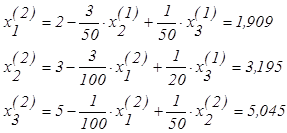
первая итерация

вторая итерация

результат третьей итерации такой же, как и у второй.

Относительная погрешность -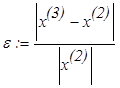 = 2,4 х 10 ^{- 5}.

4.4 Оценка погрешности метода Зейделя.

Если при всех i 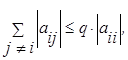q<1, тогда

. (4.4.1)

5 НАХОЖДЕНИЕ СОБСТВЕННЫХ ВЕКТОРОВ И СОБСТВЕННЫХ ЧИСЕЛ МАТРИЦ

В различных случаях возникают различные требования к информации о собственных числах и собственных векторах матриц.

1. Для решения некоторых задач механики, физики, химии требуется получение всех собственных значений, а иногда и собственных векторов матриц. Это так называемая полная проблема собственных значений.

2. Иногда нужно найти max или min по модулю собственное значение матрицы. Проблемы такого рода возникают при решении некоторых задач ядерной физики.

3. При исследовании колебательных процессов. Иногда требуется найти 2 max по модулю собственного значения матрицы, причем меньшее из них достаточно определить с меньшей точностью.

4. Там же возникают задачи отыскания собственного значения матрицы, наиболее близкого к числу λ⁰ или отыскания расстояния от числа λ⁰ до спектра матрицы.

Эти задачи называют частичными проблемами собственных значений.

5.1 Метод Крылова отыскания собственных чисел матрицы.

Данный метод основан на тождестве Гамильтона-Келли.

Так как матрица обращает в ноль свой характеристический полином, то

. (5.1.1)

Возьмем теперь произвольный вектор . 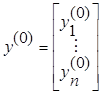и умножим на него слева равенство (5.1.1)

. (5.1.2)

Положим или тогда равенство примет вид:

. (5.1.3)

Или то же самое в матричном виде:

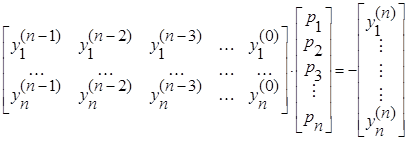. (5.1.4)

Из системы (5.1.4), вообще говоря можно найти неизвестные коэффициенты характеристического уравнения р₁… р_п..

Таким образом, определение коэффициентов характеристического многочлена сводится к решению системы линейных уравнений, причем координаты ненулевого вектора произвольны.

Например: Найдём собственные числа для матрицы 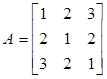. Пусть 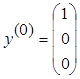, тогда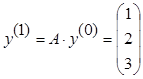

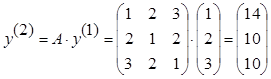
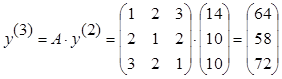Составляем систему.

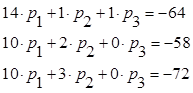
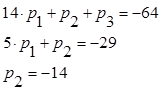
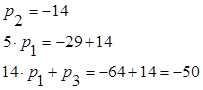
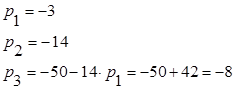
Ответ: Характеристический многочлен имеет вид:

Один из корней можно угадать . А

5.2 Вычисление собственных векторов по методу Крылова.

Ограничимся случаем, когда характеристический полином имеет различные корни λ₁, … λ_п. Предположим, что коэффициенты полинома и его корни определены. Обозначим x⁽¹⁾ … x⁽ⁿ⁾ – собственные векторы, соответствующие λ₁, … λ_п. Как и в случае развертывания определителя, возьмем вектор y⁽⁰⁾ ≠ 0. И разложим его по собственным векторам матрицы

1 2 3 4 5

Скачать файл

Итерации