Математика \ Высшая математика

Элементы теории погрешностей. Матрицы. Точные и итерационные методы решения систем линейных уравнений. Нахождение собственных векторов и собственных чисел матриц, страница 5

,                                  (5.2.1)

где . По свойству собственных векторов

 …    (5.2.2)

Тогда

                                    

…  …  …  …   …  …                                                    (5.2.3)

                                  

Определим некоторую функцию

                 (5.2.4)

Составляя линейную комбинацию из y(i) с теми же коэффициентами, получим:

               Если предположить, что

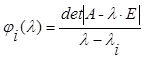                                      (5.2.5)

(остаток от деления характеристического многочлена на один из корней), то очевидно, что  и .

               Тогда от предыдущего утверждения остается, следовательно

   (5.2.6)

Итак, если Ci ≠ 0, то данная комбинация задает собственный вектор x(i) с точностью до числового множителя. Коэффициенты qij могут быть легко определены по схеме Горнера

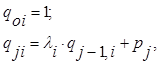                                  (5.2.7)

где собственные числа, а коэффициенты характеристического многочлена.

               Пример:Найдем собственный вектор, соответствующий = -2 (для предыдущего примера):

               Функция    значит  .

               Выражение для собственного вектора

               .

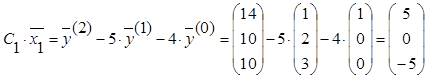               Так как собственный вектор определяется с точностью до постоянного множителя, то можно считать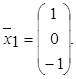

5.3.  Итерационный метод одновременного нахождения собственных значений λi и собственных векторов матрицы.

               Известно, что если А – симметрична и положительноопределенна (если все расположенные по главной диагонали миноры больше 0), то

1)  все  ;

2)  собственные векторы   и ортогональны:

                       (5.3.1)

Запишем систему, служащую для определения собственного вектора , соответствующего λ1.

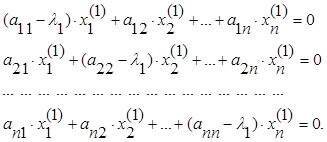       (5.3.2)

Или

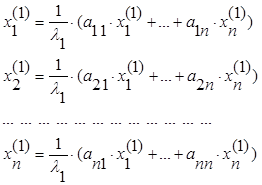        (5.3.3)

               Так как координаты вектора определяются с точностью до константы, то одну из них (например ) можно положить равной 1. И последнее уравнение в системе (5.3.3) примет вид

.                                             (5.3.4)

               Данную систему можно представить как итерационный процесс:

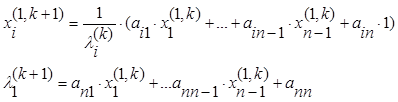      (5.3.5)

               для

               Пример: Найдём собственные числа и векторы матрицы 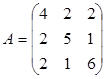 при помощи итерационного процесса.

               Покажем положительную определенность матрицы:

              .

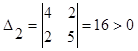
Составим систему для нахождения λi и .

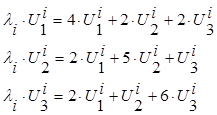
Положим = 1. Следовательно

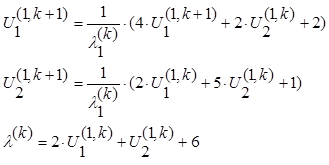
Для λ1 за нулевое приближение выбираем вектор , затем выполняем решение по схеме. .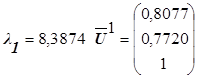

Для λ2 систему можно упростить. Из относительной ортогональности следует, что     

Положим  ,   и подставим в итерационную схему.

Третий вектор находится только по ортогональности.

5.4  Итерационный метод отыскания максимального по модулю собственного значения матрицы А.

               Для простоты полагаем наличие полной системы собственных векторов :

           .             (5.4.1)

Зададим некоторый ненулевой вектор .  Последовательно будем вычислять .

Разложим  по собственным векторам матрицы  А:    …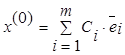      

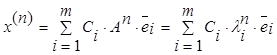
Так как выполняется условие (5.4.1), то

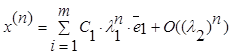.                              (5.4.2)

Вычислим скалярные произведения

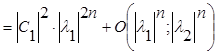.                                                       (5.4.5)

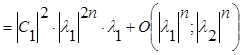.                                          (5.4.6)

               Положим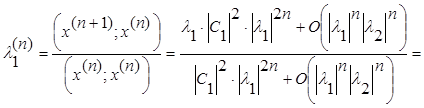 

.

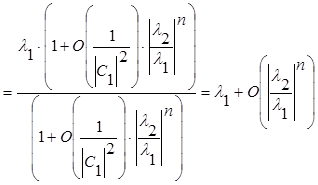Таким образом получаем итерационную схему для нахождения наибольшего собственного числа

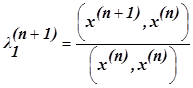                          (5.4.7)

Кроме того из (5.4.2) следует, что 

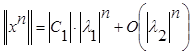.                         (5.4.8)

               Полагаем 

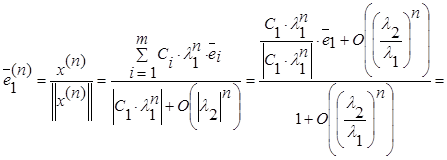
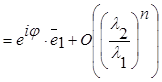,     где   

Итак, мы получили схему итерационного процесса

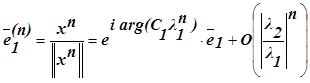.          (5.4.9)

в результате которого получаем вектор , соответствующий .

Примервычисления первого собственного числа λ1 матрицы 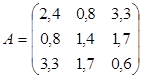  методом скалярных произведений.

Выбираем произвольный вектор 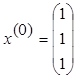 и строим последовательность векторов  ,  где.

          .

          ,

         

         

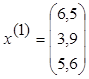
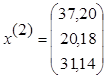
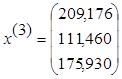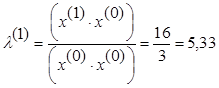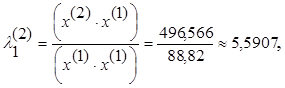
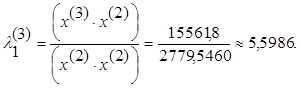
5.5  Решение полной проблемы собственных значений

при помощи QR алгоритма.

(Основа наиболее совершенных стандартных программ).

               Пусть А – произвольная вещественная матрица.

               Лемма:  Произвольная квадратная матрица может быть представлена в виде произведения ортогональной и правой треугольной  матрицы. (без доказательства).

               В среде "MathCad" это разложение выполняет функция М=gr(A).

               Аргументом ее есть исходная матрица, а результатом

М =                                                                                      

.

               Если размерность , то .

Для выделения  ортогональной Q и правой треугольной матрицы R можно воспользоваться встроенной функцией            

               Итак любую вещественную матрицу А можно представить в виде  и матрица  подобна матрице А. Составим последовательность матриц

; и ,                      (5.5.1)

тогда все матрицы  подобны между собой и подобны исходной матрице А.  Представим А в виде 

,                                               (5.5.2)

где  Λ – правая треугольная форма Жордана. Такая матрица в которой:

               , где  - собственные числа матрицы.

                при j < iи  j > i + 1, а элементы  или 1.

               Всегда можно подобрать матрицу Q так, чтобы элементы λi шли в порядке невозрастания модулей.

.

               Теорема: Пусть в разложении матрицы А все диагональные миноры матрицы Q не вырождены, тогда последовательностьматриц Ап при  п → ∞ сходится по форме к клеточному правому треугольному виду Ẵ. (Без доказательства).

               Имеется в виду, что после некоторой перестановки строк и одновременно такой же столбцов будут выполняться соотношения: если           или           k = 1,…. s.

6  ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНОГО УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ

               Пусть дано уравнение f(x)=0, предположим, что f(x) имеет только изолированные корни (т.е. для каждого корня существует некая окрестность, не содержащая других корней этого уравнения).

               Приближенное вычисление изолированных корней уравнения состоит из двух этапов:

               1) отделение корней – выделение отрезка, принадлежащего области существования функции f(x), на котором расположен только один корень;

               2) уточнение корней – вычисление их с заданной точностью.

               Процесс отделения корней уравнения основан на свойстве непрерывных функций/

Теорема (Больцано-Коши): Если непрерывная на отрезке функция f(x)  принимает на концах [а;b] значения разных знаков f(a)× f(b)< 0, то внутри [а;b] есть такое с, что f(c)=0. Этот корень будет единственным, если  существует и имеет постоянный знак  на [а;b].

6.1  Графический метод отделения корней

Скачать файл