Теория поля: Методические указания к выполнению семестрового задания (с вариантами заданий), страница 6

Проверить, является ли векторное поле вектора  потенциальным и соленоидальным. В случае потенциальности поля  найти его потенциал.

Варианты заданий:

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

17. .

18. .

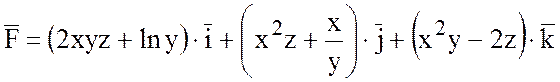19. .

20. .

21. .

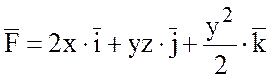22. .

23. .

24. .

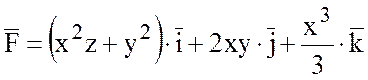25. .

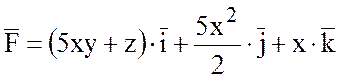Распределение вариантов по группам.

№	Группа первая				Группа вторая				Группа третья				Группа четвертая
	Задачи
	1	2	3	4	1	2	3	4	1	2	3	4	1	2	3	4
1	20	19	1	3	16	14	17	5	23	1	4	1	23	11	18	12
2	22	21	12	16	18	22	9	14	20	14	13	9	1	21	23	22
3	13	23	23	25	9	16	25	15	17	24	15	17	13	15	8	25
4	11	13	17	19	6	20	6	23	9	17	7	25	3	23	4	6
5	7	10	9	7	3	24	3	12	18	21	2	2	2	19	1	11
6	3	6	19	10	23	18	18	11	16	4	22	10	8	13	16	18
7	17	2	25	14	25	11	2	3	7	6	25	18	17	7	15	2
8	23	17	16	5	19	2	13	13	3	8	9	3	9	10	7	7
9	25	3	7	13	11	15	23	21	10	18	17	11	4	17	14	16
10	5	4	14	21	5	4	8	22	14	20	10	19	7	25	21	13
11	1	11	11	6	2	7	22	7	22	12	1	4	25	5	20	20
12	21	14	20	15	13	10	15	17	1	2	12	12	21	14	25	21
13	24	24	4	23	21	13	5	10	5	10	16	20	14	12	17	8
14	9	22	12	20	17	21	7	1	2	11	8	5	12	9	9	4
15	4	20	6	8	8	23	12	18	25	7	6	13	6	16	2	10
16	10	16	8	11	24	8	19	25	21	22	19	21	10	20	3	19
17	12	1	22	4	22	25	4	20	12	19	21	6	16	22	10	5
18	14	18	10	9	1	19	14	19	4	16	23	14	19	24	5	14
19	19	25	24	12	4	5	20	4	19	13	20	22	5	2	6	17
20	18	8	3	2	7	6	11	2	11	15	11	7	18	6	19	23
21	16	12	21	22	10	1	24	6	13	23	3	15	24	4	12	21
22	25	15	5	24	12	9	16	9	9	25	5	23	22	1	24	3
23	2	7	18	1	14	3	21	16	24	9	18	8	15	3	22	9
24	8	5	2	17	15	17	10	8	15	3	24	16	20	8	13	24
25	6	9	15	18	20	12	1	24	6	5	14	24	11	18	11	1

Литература

1. Краснов М.Л., Киселев А.И., Макаренко Г.И. Векторный анализ. – М.:Наука, 1978, - 158 с.

2. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. – М.:Наука, 1968, - 735 с.

3. Берман Г.Н. Сборник задач по курсу математического анализа. – М.:Наука, 1977, - 416 с.

4. Кальницкий Л.А., Добротин Д.А., Жевержеев В.Ф. Специальный курс высшей математики. – М.:Высш. шк., 1976. – 346 с.

5. Кудрявцев Л.Д. Математический анализ, том 2. – М.:Высш. шк., 1973 – 520 с.