Математика \ Высшая математика

Теория поля: Методические указания к выполнению семестрового задания (с вариантами заданий), страница 5

, .

Тогда

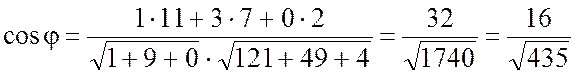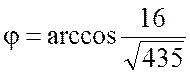Ответ: .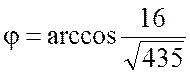

б) Найти производную скалярного поля 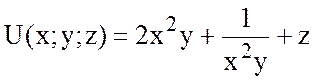в точке А(1;1;-1) по направлению от точки А к точке В(-1;1;0).

Решение.

Производная по направлению находится по формуле:

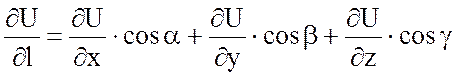Найдем частные производные:

; ; .

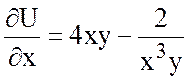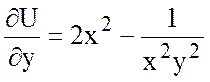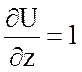Найдем значения частных производных в точке А(1;1;-1)

, , .

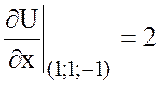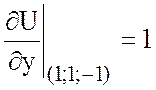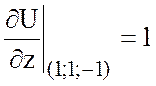Направление совпадает с вектором

Направляющие косинусы вектора найдем по формулам:

Если , то его направляющие косинусы будут равны:

;

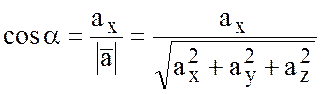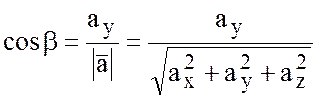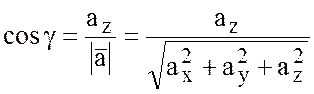Тогда для вектора направляющие косинусы будут такими:

, , .

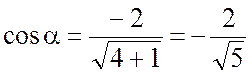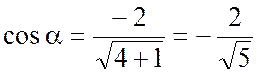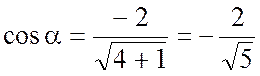Тогда

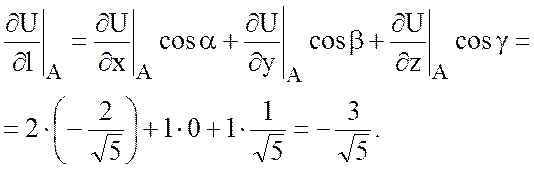
Ответ: .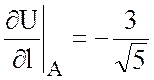

Задача 2.

а) Вычислить поток векторного поля

через треугольник, вырезанный из плоскости координатными плоскостями, в том направлении нормали к плоскости, которое образует с осью OZ острый угол.

Решение.

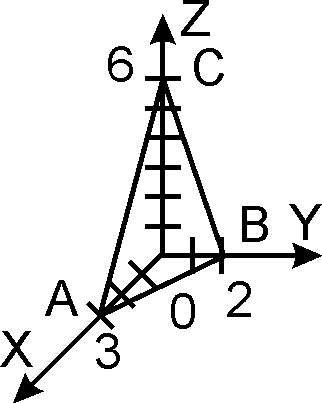
Рисунок 18

На рисунке показан треугольник, через который вычисляется поток.

Найдем орт нормали :

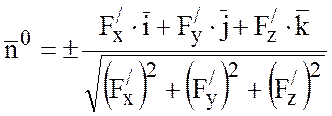У нас F(x;y;z)=2x+3y+z-6, тогда

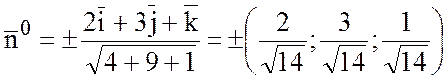Выберем знак «+», так как по условию задачи угол острый и , тогда

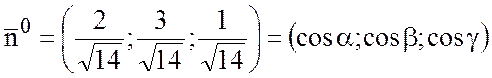Найдем :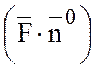

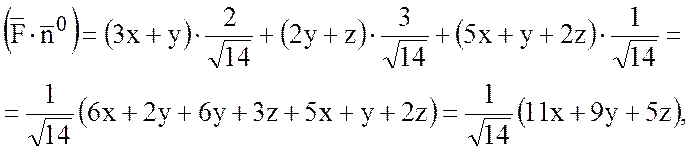
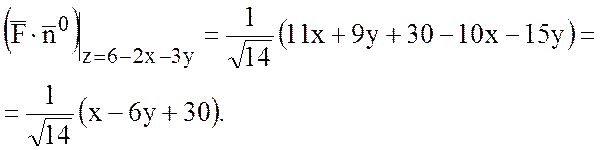
Поток найдем по формуле:

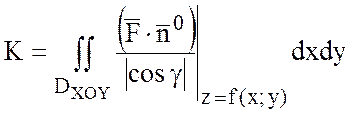То есть проектированием на плоскость XOY.

Спроектировав АВС (рис. 18) на плоскость XOY, получим АОВ, уравнение АВ:

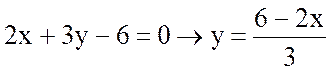Тогда

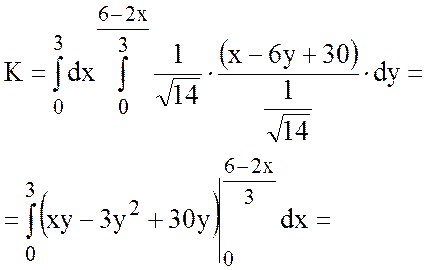
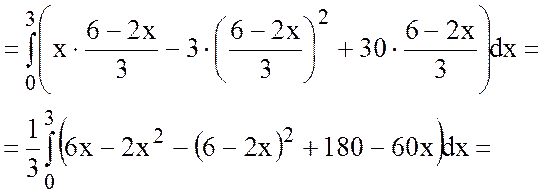
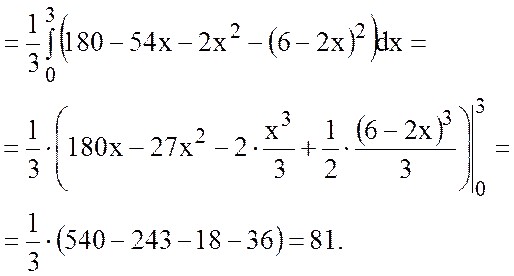
Ответ: К=81.

Задача 2.

б) Найти дивергенцию и ротор векторного поля .

Решение.

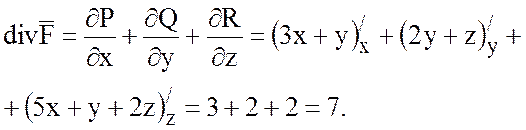
Задача 3.

а) Найти поток вектора через внешнюю поверхность пирамиды, образованной плоскостью Р и координатными плоскостями непосредственно и по формуле Остроградского – Гаусса.

Найдем поток векторного поля непосредственно.

Согласно свойству аддитивности поток через внешнюю поверхность пирамиды равен сумме потоков через все четыре грани пирамиды.

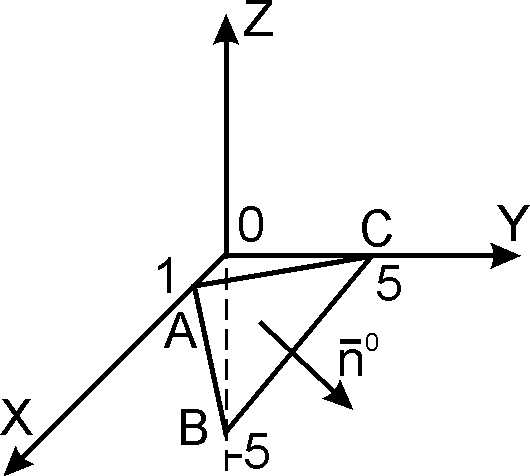
Рисунок 19

где - поток через грань ОАВ,

- поток через грань ОСВ,

- поток через грань ОАС,

- поток через грань АВС

Найдем - поток через ОАВ. Уравнение ОАВ: y=0. Внешняя нормаль к грани ОАВ . Тогда . Следовательно, =0.

Найдем - поток через грань ОСВ. Уравнение ОСВ: x=0. Внешняя нормаль к грани ОСВ , .

Тогда и .

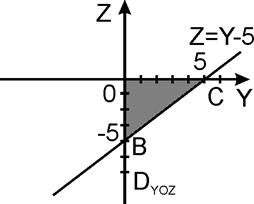
Рисунок 20

Найдем - поток через ОАС. Уравнение ОАС: z=0.

Внешняя нормаль . Тогда и =0.

Найдем - поток через грань АВС. Найдем внешнюю по отношению к пирамиде нормаль к грани АВС:

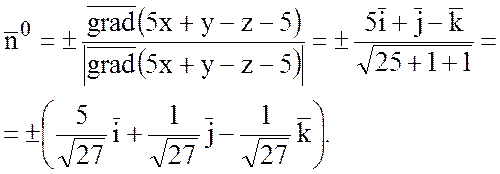
Так как образует тупой угол с осью OZ, то выбираем знак «+», чтобы .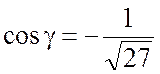

Тогда

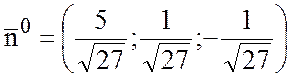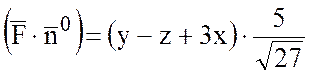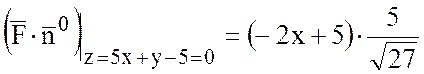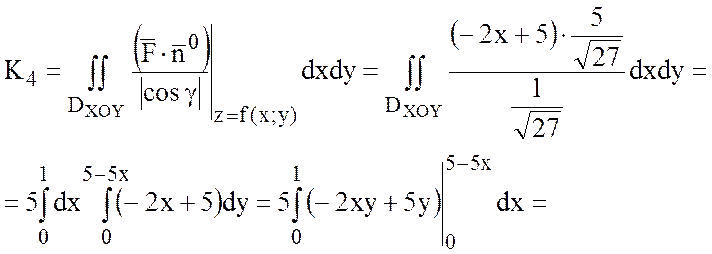
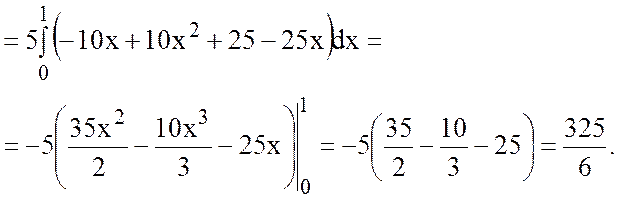
Тогда поток через внешнюю поверхность пирамиды

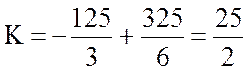Найдем теперь поток через поверхность пирамиды по формуле Остроградского – Гаусса:

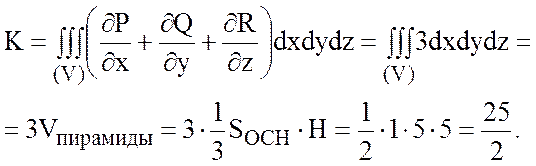
б) Найти циркуляцию векторного поля непосредственно и по формуле Стокса вдоль линии пересечения плоскости Р с координатными плоскостями.

, .

Решение.

Найдем циркуляцию непосредственно по определению

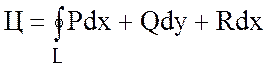Так как L представляет собой стороны треугольника АВС (рис. ) и Q=R=0, то

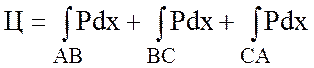AB: y=0, 5x-z=5, z=5x-5,

BC: x=0, dx=0,

CA: z=0, 5x+y=5, y=5-5x.

Тогда

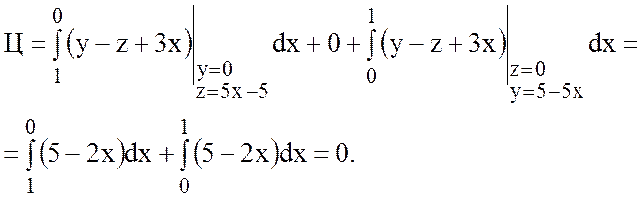
Найдем теперь циркуляцию по формуле Стокса:

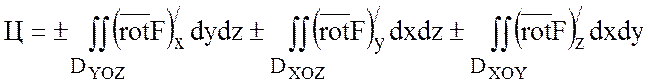Плоскость 5x+y-z-5=0 имеет .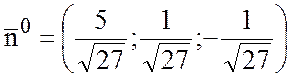

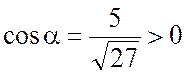Тогда в формуле Стокса у первых 2-х слагаемых «+», так как , где , , где .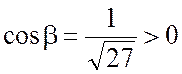

У третьего слагаемого выбираем «-», так как , так как .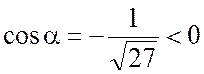

Тогда

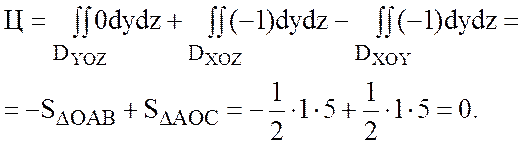
Задача 4

Проверить, будет ли поле вектора потенциальным и соленоидным. В случае, если поле потенциально, найти его потенциал.

Решение.

Поле вектора потенциально, если =0. Найдем :

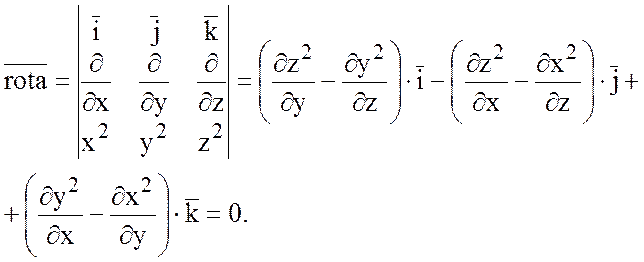
Так как =0, то поле вектора потенциально. Поле вектора соленоидально, если =0.

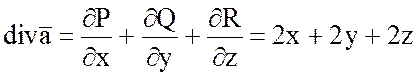Так как во всех точках поля, то поле вектора не является соленоидальным.

Найдем потенциал потенциального поля .

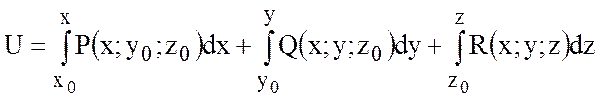В качестве точки возьмем точку (0;0;0). Тогда

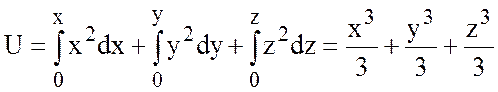Проверка:

, , .

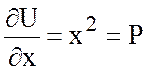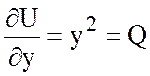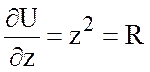17 Семестровое задание по теме «Теория поля»

Задача 1.

а) Найти угол между градиентами функции в точках А и В.

б) Найти производную функции в точке А по направлению из точки А в точку В.

Варианты заданий:

1. , А(1;2;-1), В(0;1;-3).

2. , А(1;2;0), В(4;1;2).

3. 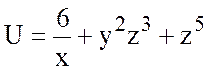, А(1;-1;0), В(-1;2;1).

4. , А(0;5;1), В(1;1;-1).

5. 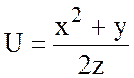, А(1;0;1), В(0;1;-1).

6. 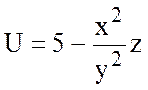, А(1;-1;1), В(2;1;2).

7. , А(0;1;2), В(1;2;1).

8. , А(1;0;1), В(-1;1;2).

9. 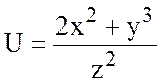, А(1;2;1), В(-1;1;2).

10. , А(1;1;1), В(2;1;-1).

11. 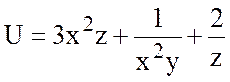, А(1;-1;1), В(-1;1;2).

12. 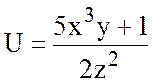, А(1;-1;1), В(2;1;2).

13. 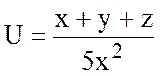, А(1;0;1), В(2;1;-1).

14. , А(1;-1;1), В(0;1;2).

15. 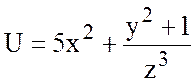, А(1;2;1), В(0;1;-1).

16. 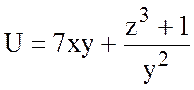, А(1;1;-1), В(0;2;1).

17. , А(1;1;2), В(0;-1;1).

18. 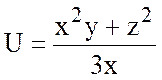, А(1;1;2), В(-1;0;1).

19. 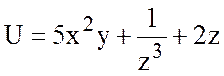, А(1;2;-1), В(2;1;1).

20. , А(0;1;2), В(-1;2;1).

21. 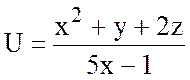, А(1;1;1), В(0;1;-1).

22. 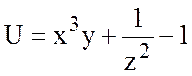, А(1;1;-1), В(1;2;1).

23. 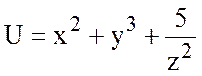, А(0;1;1), В(1;2;-1).

24. , А(1;2;1), В(0;1;-1).

25. 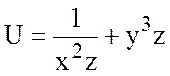, А(1;1;-1), В(-1;2;1).

Задача 2.

а) Найти поток векторного поля через треугольник, вырезанный из плоскости Р координатными плоскостями, в том направлении нормали к плоскости, которое образует с осью OZ острый угол.