Елементи теорії функцій комплексної змінної. Інтегральне перетворення Лапласа. Дискретне перетворення Лапласа, страница 2

          Число R називається радіусом збіжності степеневого ряду і визначається по формулі

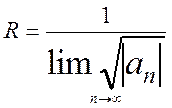                                                      (11)

          Найпростішим степеневим рядом є геометрична прогресія

                                         (12)                                             

          Ряд (12) збігається при  і його сума дорівнює

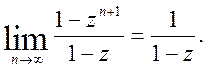
          ТЕОРЕМА 2. (Вейєрштраса). Якщо члени ряда

                                  (13)                                          

що рівномірно збігається всередині області D, аналітичні функції в цій області, то сума ряда f(z) також є аналітичною функцією в області D. Крім цього ряди

                                 (14)

отримані шляхом к – кратного диференціювання ряда (13), також збігаються рівномірно всередині D і являють собою похідні к – ого порядку від суми ряда f(z).

          ТЕОРЕМА 3. Довільна функція f(z), аналітична в деякому крузі  з центром в точці  , може бути зображена всередині цього круга рядом Тейлора

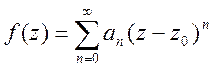                              ,                   (15)

де 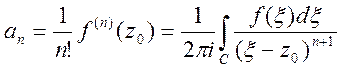                           (16)

і таке зображення єдине. Тут - коло з центром  і радіусом

          Доведення. На основі інтегральної формули коші (8) для довільої точки , маємо

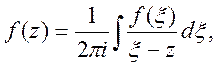
де точка z лежить всередині контура . На  маємо  а з другого боку  так як z лежить всередині

          Використаємо розкладення

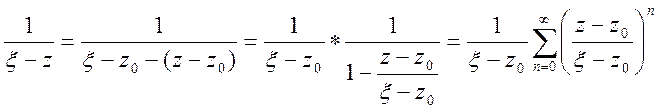так як 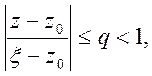 то останній ряд збігається рівномірно відносно

           Далі

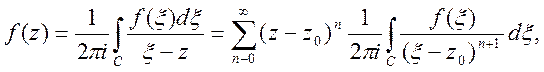
         або              f(z)=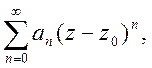

де 

          

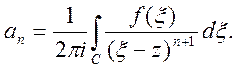
          Доведення єдності приводити не будемо.

          Означення. Функція, ряд Тейлора якої збігається при довільних z, називається цілою функцією.

        1.4 Ряди Лорана  і особливі точки

          Розглянемо функції комплексної змінної, які не являються аналітичними у всіх точках області визначення. Точки, в яких не виконують умови Коші – Рімана (2) будемо називати особливими. Нехай однозначна аналітична функція f(z) задана на області D, яка обмежена двома концентричними колами з радіусами R і r (R>r>0) з центром у точці . Виберемо два концентричні кола (рис. 2)  і  з центром в  і радіусами  і  відповідно .

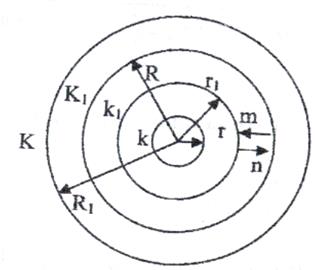
        Рис. 2

Перетворюючи двозв'язну область , обмежену колами  і  в одно зв’язкову за допомогою розрізу mn і застосовуючи інтегральну формулу mn, будемо мати

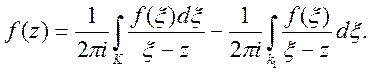                            (17)                            

          У першому інтегралі використаємо розкладення 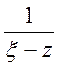 у ряд 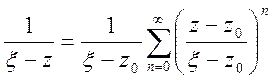, що збігається рівномірно відносно

          У другому інтегралі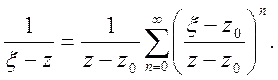

          Далі, використовуючи ці ряди і формулу (17), одержимо

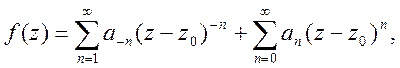                        (18)         

де

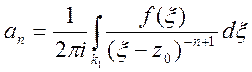 (n=1,2,...)

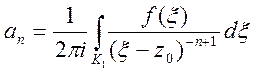          (n=0,1,2,…)               (19)

Розкладання (18) з коефіцієнтами (19) називається рядом Лорана. Для аналітичної всередині D функції контури інтегрування  і  можна замінити одним контуром .

          Фактично ми довели слідуючу теорему.

          ТЕОРЕМА 1. (Лоран). Кожна функція f(z), аналітична в області D: r< зображуються в цій області рядом Лорана

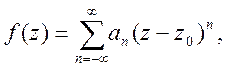                                              (20)

де

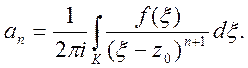                                             (21)

          Означення. Ряд 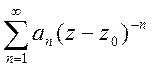 називається головною частиною ряду Лорана, а ряд 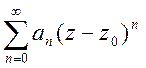  – правильною частиною ряду Лорана.

          Означення. Точка  називається полюсом m – ого порядку, якщо головна частина ряду Лорана містить скінчене число членів, при цьому . Якщо число членів нескінчене, то точка  називається істотно особливою точкою.

          Означення. Функція f(z) називається меломорфною, якщо її особливі точки є полюси і тільки вони.

          Розкладання функції f(z) в області  у ряд Лорана має вигляд

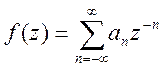                                                         (22)

          Приклад. Знайти ряд Лорана для функції

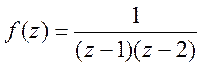 в області D:

          Функція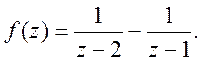  

          Далі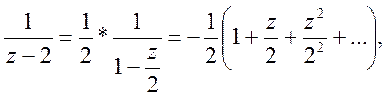

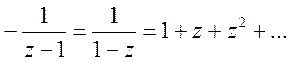
          Звідси .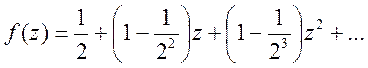

Вправи. Розкласти функції  у ряд Лорана:

          1. 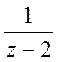 в околі точок z=0 i z=.

          2. 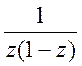 в околі точок .

          3. 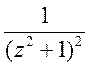 в околі точок  і .

        1.5 Теорема Коші про лишки

          ТЕОРЕМА. Якщо однозначна функція f(z) аналітична в точці і в деякому її околі,то

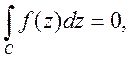
де С – довільний контур із названого околу, що містить всередині точку

          Хай точка  особлива ізольована точка функції f(z). Тоді в околі  функція f(z) може бути зображена рядом Лорана

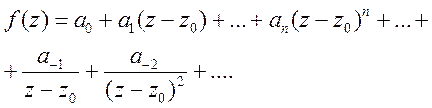
          Інтегруючи цей ряд і приймаючи до уваги, що

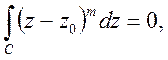 m=0, 1, 2, …,

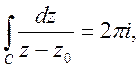
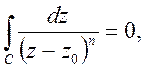 n=2, 3, …,

одержимо

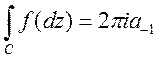                                                            (23)

        Означення. Значення інтеграла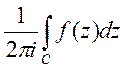назива-

ється лишком функції відносно особливої точки .

        Відповідно до формули (23) лишок функції f(z) дорівнює коефіцієнту . Лишок далі будемо позначати символом res f(z).

        Хай точка  є полюс першого порядку. Використовуючи ряд Лорана, знайдемо

або

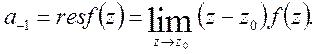                                         (24)

        Аналогічним чином, якщо точка  є полюсом m – ого порядку, то

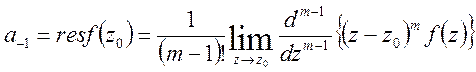                 (25)

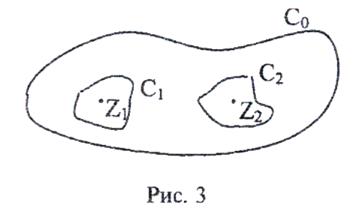
Розглянемо основні теореми про лишки. Хай в області аналітичності D функції f(z) маємо замкнений контур  (рис. 3), всередині якого функція f(z) має скінчене число ізольованих особливих точок  (v=1,2,…n). Розташуємо кожну із точок  всередину достатньо малих замкнених контурів , що повністю лежать всередині контуру .

        ТЕОРЕМА. Інтеграл від функції f(z), взятий по замкненому контуру , в додатному напрямку (при цьому  належить області D, де функція однозначна і аналітична, за виключенням скінченого числа ізольованих особливих точок), дорівнює помножений на  сумі лишків функції відносно усіх особливих точок всередині , тобто 

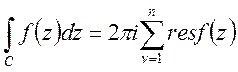                                                   (26)

        Приклад. Знайти лишок функції 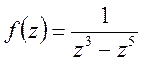  відносно точки z=1.

        Точка z=1 є полюс функції f(z) першого порядку. Відповідно формули (24) маємо:

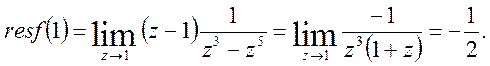
        Вправа. Знайти лишки функції f(z) відносно всіх особливих точок

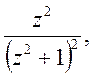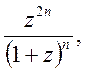        1)  2)  3)  

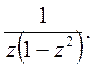
      1.6 Питання для повторення матеріалу