Елементи теорії функцій комплексної змінної. Інтегральне перетворення Лапласа. Дискретне перетворення Лапласа, страница 3

1. Що таке замкнена область?

        2. Що таке однозв´язана область?

        3. Що таке функція комплексної змінної?

        4. назвіть умови Коші – Рімана.

        5. Перелікуйте основні властивості аналітичних функцій.

        6. дайте означення інтегралу функції комплексної змінної.

        7. Приведіть формулу Коші. Який зв’язок існує між похідною f(z) і значенням функцій f(z) на контурі C?

        8. Що називається рядом Тейлора?

        9. Приведіть розкладання функції f(z) в ряд Лорана. Як обчислюють коефіцієнти цього ряду?

        10. Що таке лишок функції?

        11. Сформулюйте теорему Коші про лишки.

                                                                                      

2. ІНТЕГРАЛЬНЕ ПЕРЕТВОРЕННЯ

ЛАПЛАСА

      2.1. Означення перетворення Лапласа

Означення. Функцією екс потенційного типу називається функція f(t) дійсної змінної t, для якої виконується не рівняння

                                                                     (1)

де M>0, . Число  називається показником зростання функції f(t).

        Означення. Перетворенням Лапласа функції дійсної змінної f(t) називається функція комплексної змінної F(p), яка визначається формулою

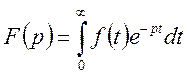                                                             (2)

        При цьому функція f(t) повинна відповідати трьом умовам:

1)  функція f(t) – Кусково – неперервна при , тобто вона має скінчене число точок розриву першого роду;

2)  функція f(t) дорівнює нулю при відُємних аргументах t

                                                            (3)

3)  функція f(t) є функцією екс потенційного типу.

        Функцію f(t) далі будемо називати оригіналом, а F(p) – зображенням. Відповідність між оригіналом і зображенням записується у вигляді:

або 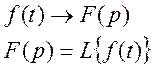                                                           (4)

        ТЕОРЕМА 1. Для усякого оригіналу f(t) зображення F(p) існує на півплощині Rep=s>, при цьому функція f(p) аналітична у названій півплощині.

        Доведення. Доведемо спочатку існування оригіналу. Нехай  точка на півплощині . Тоді мають місце співвідношення

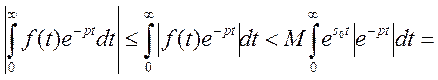
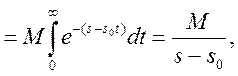                                                 (5)    

  так як,  Звідси випливає факт існування і однозначності зображення F(p).

        Щоб довести аналітичність F(p) у півплощині  досить довести існування похідної   Хай знову  довільна точка півплощини  Знайдемо

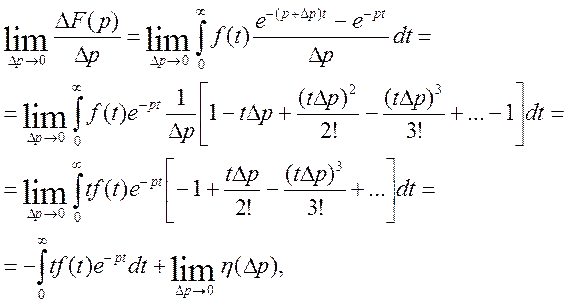
де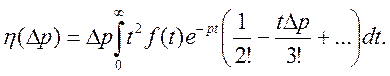

        Доведемо, що  при  Маємо

        

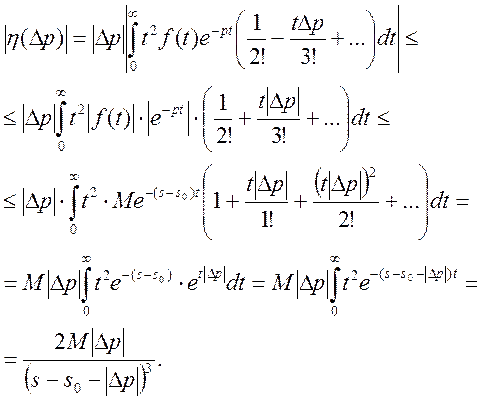
        Тобто 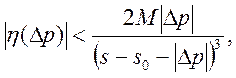 звідки випливає, що  при . Таким чином, доведено існування похідної функції F(p):

                          

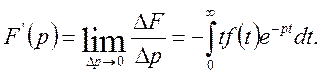
                 (7)             

        Теорема існування зображення F(p) повністю доведена.

        В и с н о в о к. Якщо точка  так, що , то зображення F(p).

        Справедливість цього твердження випливає із не рівняння (5).

        Можна також довести теорему єдності зображення.

        ТЕОРЕМА 2. Якщо F(p) є зображенням двох оригіналів, і  то ці оригінали збігаються один з одним у всіх точках, в яких вони неперервні.

        Розглянемо деякі приклади на знаходження зображення.

        Приклад 1. Хай  - одинична функція Хевісада.

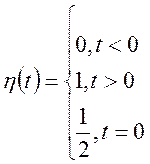                                                                     (8)

        Знайти зображення для функції (8). Відповідно до формули (2)

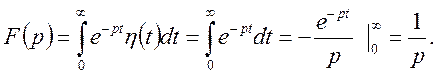
        Даний інтеграл існує в області . Таким чином,

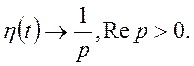
        У звُ язку з тим, що кожний оригінал при  дорівнює нулю, то для простоти замість функції

 

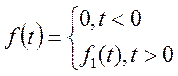
будемо записувати  Так запис  означає функцію

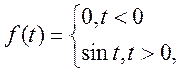
а для функції Хевісада має місце формула

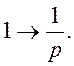                                    (9)

        
        Приклад 2. знайти зображення для функції  де  - довільне комплексне число.

        Відповідно до формули (2) маємо

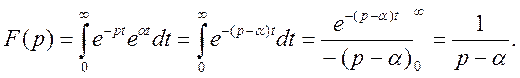
        Даний інтеграл існує, якщо  

        Таким чином,

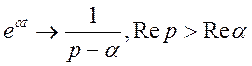                                                (10)

Вправи. Використовуючи означення перетворення Лапласа, знайти зображення функцій

      

      2.2 Лінійність перетворення Лапласа. Теорема

      подібності

        ТЕОРЕМА 1. (лінійність перетворення).Якщо оригіналам  відповідають зображенням  то

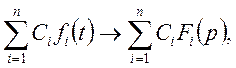                                                         (11)

де - довільні постійні.

        Доведення. При доведенні скористаємося властивістю лінійності операції інтегрування. Маємо

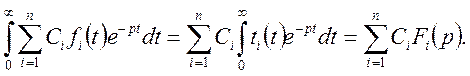
        Теорему доведено.

        Приклад 1.

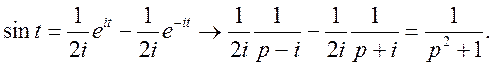
        Приклад 2.

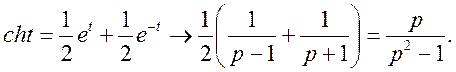
        Теорема, що приводиться далі, дає відповідь про вплив зміни масштабу змінної t на зображення F(p).

        ТЕОРЕМА 2 (подібність перетворення). Якщо  і с довільне додатне число, то

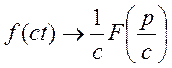
                                                             (12)

        Доведення. Знайдемо зображення оригіналу f(ct)

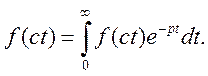
        Зробимо в цьому інтегралі підставку  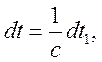 будемо мати

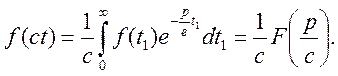
        теорему доведено.

        Приклад 3. Використавши зображення для sin t знайти зображення для оригіналу f(t)=sint.

        Маємо 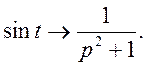 Знайдемо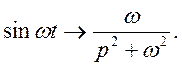

Таким чином,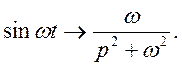

        Приклад 4. Використавши теореми лінійності і подібності зображення Лапласа, знайти зображення для функції

        Маємо

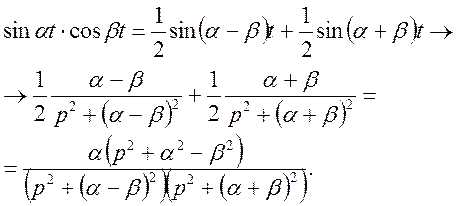
таким чином,

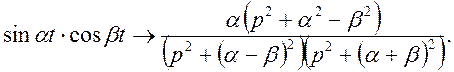
        Вправи. Використовуючи теореми лінійності і подібності знайти зображення функцій.

        1) cost t     2) sh t     3) ch t+cost        4) sin+sh t

        5) cosωt     6) shωt   7) chωt               8)

        9) cos   10)     11)

        12)              13) .

      2.3. Теореми запізнення, випередження і зсунення

        Розглянемо функцію

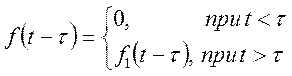
де  - додатне число.

        Графік функції  зсунутий відносно графіка функції  праворуч вісі  на величину .

        Розглянемо відповідну теорему.

        ТЕОРЕМА 1 (запізнення). Якщо τ – додатне число і  то

                                                        (13)

        Доведення. Зробимо заміну змінних , будемо мати

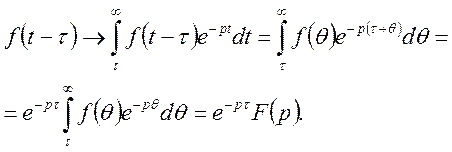
       Теорему доведено.

        Означення. Функцію 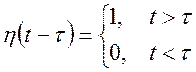 будемо називати узагальненою функцією Хевісайда.

        Приклад 1. Знайти зображення функції