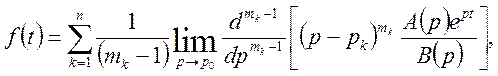Елементи теорії функцій комплексної змінної. Інтегральне перетворення Лапласа. Дискретне перетворення Лапласа, страница 6

                        (38)

де  - кратність кореня  багаточлена В(р).

        Якщо багаточлен В(р) має лише прості корені, то формулу (38) можна представити так

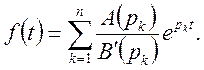                                                              (39)

        Приклад 1. Знаючи зображення 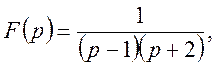 знайти оригінал f(t).

        В цьому прикладі А(р)=1, В(р)=(р - 1)(р + 2).

        Корені знаменника

        На основі формули (39) будемо мати

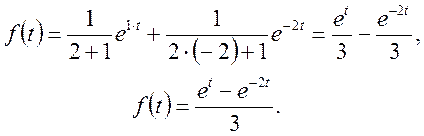
        Приклад 2. Відомо 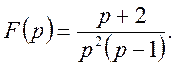 Знайти оригінал f(t).

        Знаменник цієї раціональної функції має однократний корінь  і двократний корінь .

        Відповідно до формули (38) будемо мати

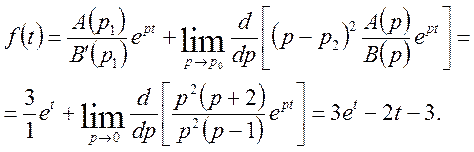
        Таким чином

        З а у в а ж е н н я. Якщо відомо зображення функції F(p) у вигляді суми найпростіших дробів, то не обов’язково застосовувати для знаходження оригіналу f(t) формули розкладення (38), (39). У цьому випадку можна скористатися уже відомими зображеннями. Пояснимо на прикладі.

        Приклад 3. Для функції  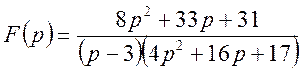знайти оригінал f(t).

        Запишемо функцію F(p) у вигляді суми найпростіших дробів:

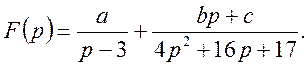
        Находячи числа a, b, c способом невизначених коефіцієнтів маємо a=2, b=0, c=1:

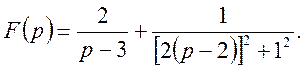
        Відомо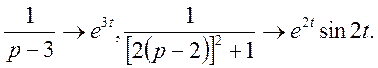

        Застосовуючи теорему лінійності зображення одержуємо

        Таким чином,

        Вправи. Знаючи зображення F(p), знайти оригінал f(р):

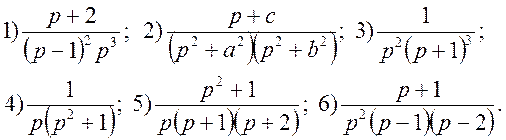
      2.13 Множення оригіналів

        ТЕОРЕМА. Якщо  то

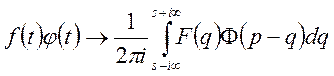                                           (40)

        Доведення. Будемо мати

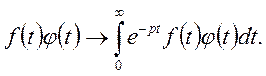
        Під знаком інтегралу замінимо функцію f(t) по формулі обернення (36):

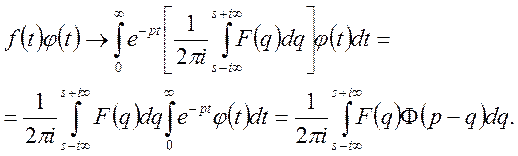
        Остаточно

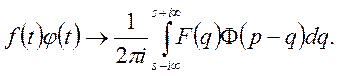
        Теорему доведено.

        Таким чином добутку двох оригіналі відповідає згортка їх зображень. Теорему множення можна використовувати при знаходженні інтегралів

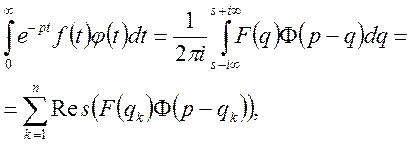
або                                                     

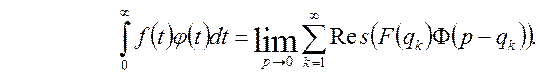
        Приклад. Обчислити невласний інтеграл

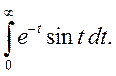
        Позначимо Маємо

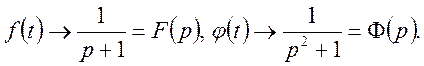
        Функція F(p) має простий полюс  Застосуємо до інтегралу формулу (41)

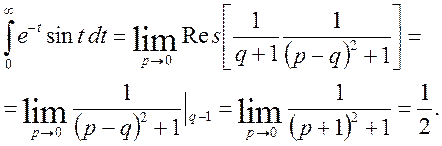
        Остаточно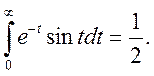

        Вправи. Обчислити невласні інтеграли

 

       

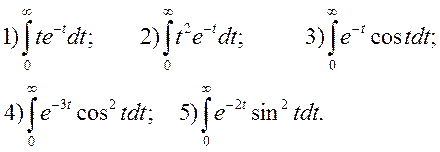
      2.14 Використання перетворення Лапласа при розв’язанні  диференціальних рівнянь

Нехай подано рівняння n-го порядку:

                                       (42)

        Із початковими умовами

                                     (43)

Застосуємо перетворення Лапласа до Формул (42), (43). Будемо мати:

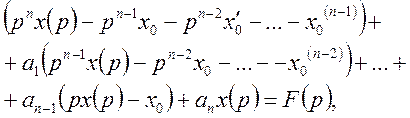
де                        

        Звідки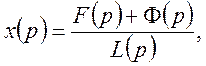

де а Ф(р) – багаточлен ступеня ще вище, ніж (n - 1), з коефіцієнтами, що залежать від початкових умов.

        Розглянемо приклад.
        Приклад 1. Знайти розв’язок  рівняння

задовольняючи початковим умовам

        Вважаючи  і знаходячи 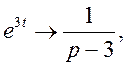отримаємо операторне рівняння

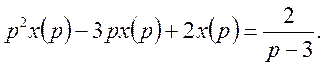
        Звідки

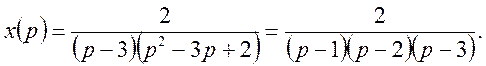
             Знаходячи по зображенню оригінал, будемо мати

        Для розв’язку диференціальних рівнянь можна використовувати також інтеграл Дюамеля.
        Нехай потрібно знайти розв’язок Диференціального рівняння (42) із нульовими початковими умовами

                                                 (44)

        Розглянемо допоміжні диференціальні рівняння

                                           (45)

        Перейдемо у рівняннях (42), (45) до зображень

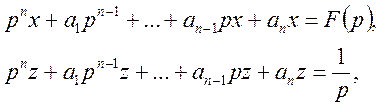
звідки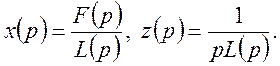  

        Із двох останніх співвідношень знаходимо

і, використовуючи формулу (34), одержимо розв’язок

рівняння (42) у вигляді

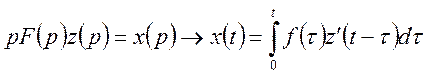                              (46)

        Приклад 2. Знайти розв’язання диференціального рівняння  з початковими умовами  

        Знайдемо спочатку розв’язання рівняння  що задовольняє умовам  Рівняння у зображеннях має вигляд:

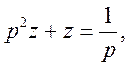
        Звідки 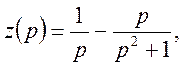а, значить . Для знаходження x(t) застосуємо формулу (46), у нашому випадку так що

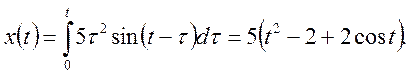
        На завершенні, розглянемо ще два приклади.

        Приклад 3. Знайти розв’язок диференціального рівняння з Кусково-неперервною правою частиною:

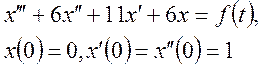
де

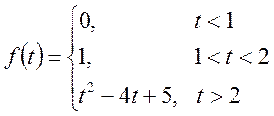
        За допомогою функції Хевісада  функцію  представимо так

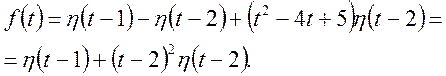
        Маємо

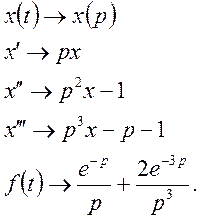
        Отримаємо операторне рівняння

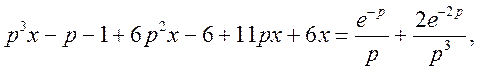
або

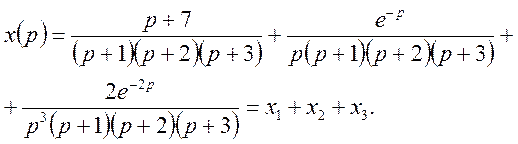
        Для знаходження оригіналів використаємо формули розкладання (38), (39). Функція  має полюси

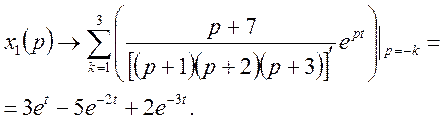
        Аналогічно для  будемо мати

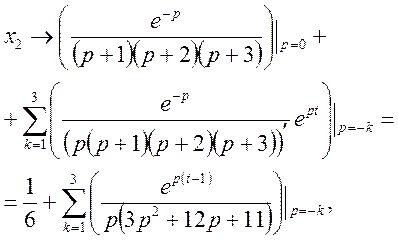
або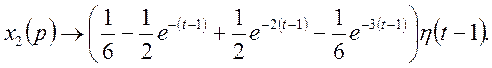        

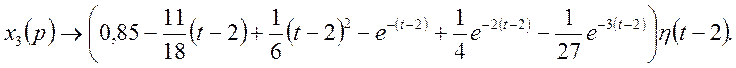
остаточно маємо

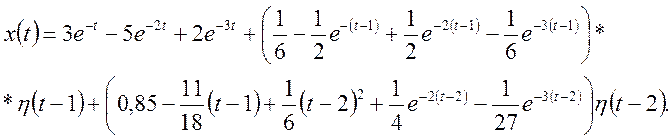
        Приклад 4. Знайти розв’язок системи рівнянь:

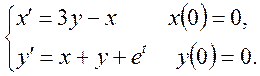
        Нехай  Отримаємо систему оператор них рівнянь:

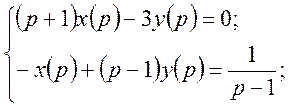
Розв’язок цієї системи має вигляд

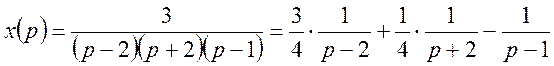
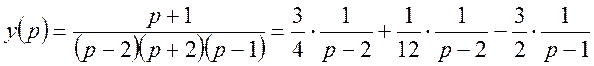
Повертаючись до оригіналів, одержимо

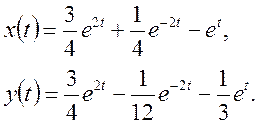
        Вправи.

         1. Розв’язати диференціальні рівняння, застосовуючи перетворення Лапласа

       

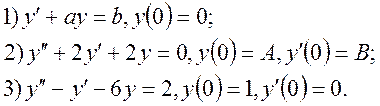
        2. За допомогою перетворення Лапласа розв’язати диференціальне рівняння, права частина якого є кусково-неперервна функція:

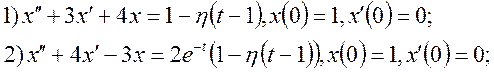
        3) Застосовуючи інтеграл Дюамеля знайти розв’язок диференціальних рівнянь.

         

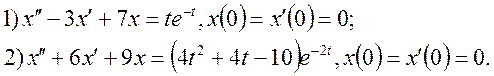
        За допомогою перетворення Лапласа знайти розв’язок систем лінійних диференціальних рівнянь:

 

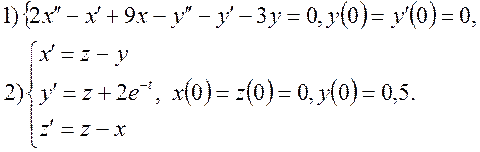
        2.15 Застосовування перетворення Лапласа до розв’язку рівнянь з частинними похідними.

        Як приклад, розглянемо застосування перетворення Лапласа у задачах тривимірної теорії пружності. Напружений стан ізотропної пластини описується системою рівнянь з частинними похідними:

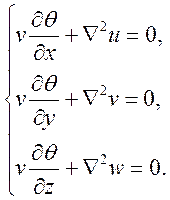                                                                         (47)

        Тут u, v, w – переміщення.

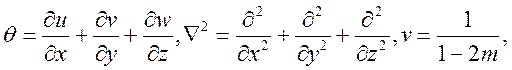
m – коефіцієнт Пуасона.

        Введемо слідуючи позначення:

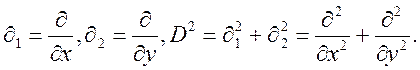
        Тоді система (47) прийме вигляд:

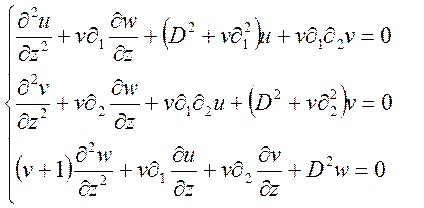                                    (48)

        Формально вважаємо в системі (48)  постійними величинами і розглядаємо останню, як систему звичайних диференціальних рівнянь по змінній z. Застосуємо до системи (48) перетворення Лапласа.

        Будемо мати

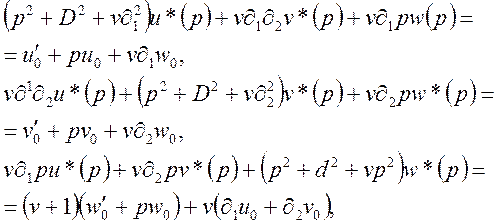
де                              

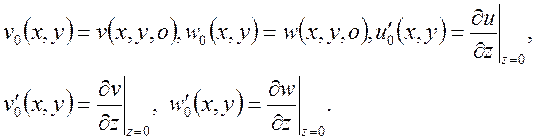
Із системи (49) знаходимо

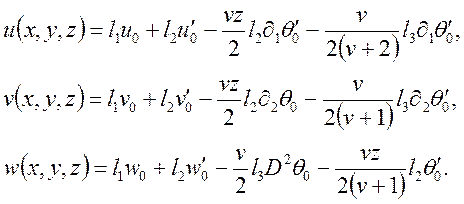                        (50)

        Символами  позначенні оператори

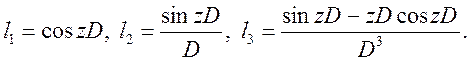
        Розкладаючи ці функції в ряд по степенях zD бачимо, що оператори є цілі функції відносно оператора .