Елементи теорії функцій комплексної змінної. Інтегральне перетворення Лапласа. Дискретне перетворення Лапласа, страница 5

        Вправи. Використовуючи теореми інтегрування і диференціювання зображення, знайти зображення для функції:

       

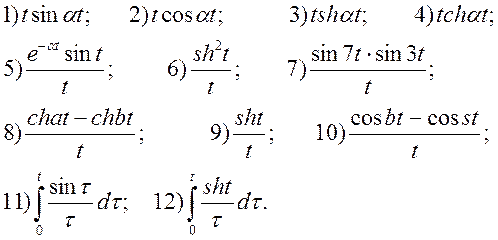
        2.7 Граничні теореми

        ТЕОРЕМА 1. Якщо , а  - оригінал, то

                                                         (26)

при умові, що остання границя існує.

       Доведення. Так як  - оригінал, то йому відповідає зображення

        Для зображення має місце рівність

або                               

        Теорему доведено.

        ТЕОРЕМА 2. Якщо  - оригінал і існує  то

                                                        (27)

        Доведення. Із умови, що - оригінал випливає, що

 або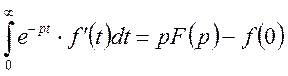              

        Знайдемо в останній рівності межу при . Будемо мати

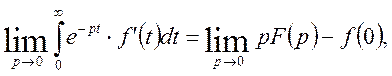
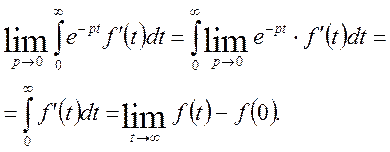
        Тобто  

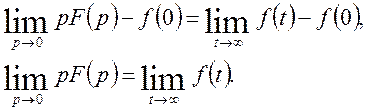
або

        Теорему доведено.

      2.8 Згортка функцій

        Означення. Згорткою двох неперервних функцій  і f(t),  називають функцію , що визначається інтегралом

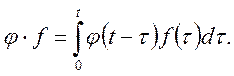                                                         (28)

        Таким чином згортка є дія, що парі функцій ставить у відповідність одну єдину  функцію. Операція отримання згортки називається згортанням функції.

        Приклад. Знайти згортку функцій Хевісайда

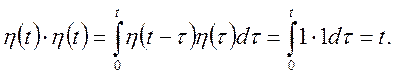
        ТЕОРЕМА 1. Для згортки мають місце співвідношення:

1)  комутативність:

                                                                       (29)

2)  асоціативність:

                                                      (30)

3) дистрибутивність:

                                                       (31)

     4)                                  

        Доведення. При доведенні цієї теореми обмежимося пунктом 1. Розглянемо інтеграл

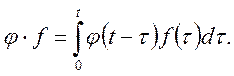
        Зробимо заміну змінних . Будемо мати

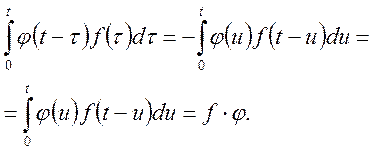
        Теорему доведено.

        Сформулюємо без доведення ще дві теореми про властивості згортки функцій.

        ТЕОРЕМА2. Якщо f(t) і  неперервні функції при  то їх згортка також неперервна функція при .

        ТЕОРЕМА3. Якщо f(t) і  неперервні функції при  і , то хоч би одна із функцій при  дорівнює нулю.

        Теорема 3 ще носить назву теореми Тімчмарша.

        Вправи. Знайти згортку функцій.

        

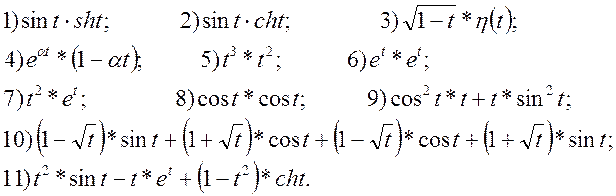
      2.9 Множення зображень

        ТЕОРЕМА 1.Якщо f(t) і  - оригінали, то згортка  також є оригінал.

        Доведення. Очевидно, що функція  є кусково – неперервна і  при t < 0. Доведемо, що  - функція екс потенційного типу.

        Із умови теореми де для визначеності .

        На основі цих рівнянь маємо

де

        Так як, , то  з сили довільності .

        Теорему доведено.

        ТЕОРЕМА 2 (Бореля). Якщо  то

                                                                (33)  

        Доведення.

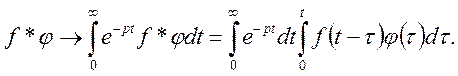
        В цьому рівнянні двократний інтеграл обчислюється по області D (рис. 11).

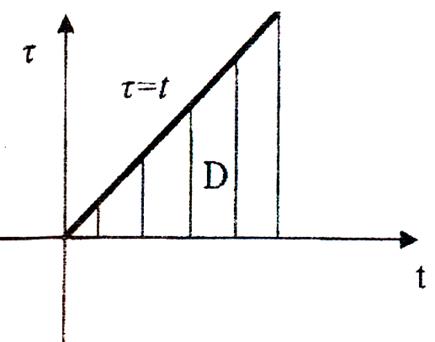
Рис. 11

        Поміняємо порядок інтегрування

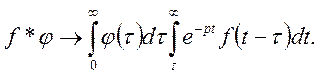
        Вважаючи  отримаємо

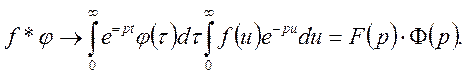
        Теорему доведено.

        Приклад 1. Знайти оригінал по зображенню

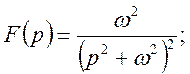
        Маємо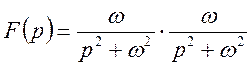

        Відомо, що 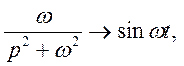тому

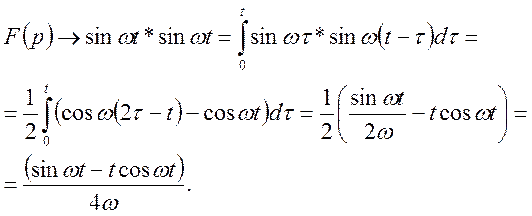
таким чином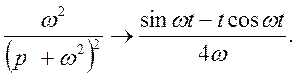

        Приклад 2. Найти оригінал для зображення

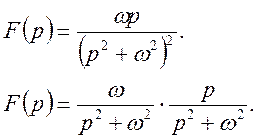
        Відомо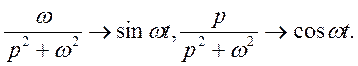

        По теоремі множення зображень:

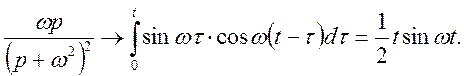
        Приклад 3. Найти оригінал по зображенню

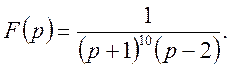
        Застосовуючи до зображення функції  теореми диференціювання зображення і зсунення будемо мати

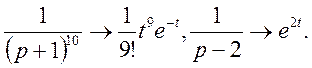
        Далі по теоремі множення отримуємо

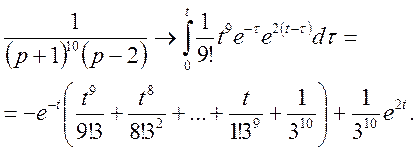
        Вправи. Знайти оригінали для функцій

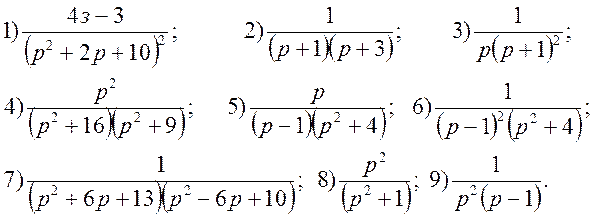
        2.10 Інтеграл Дюамеля

        ТЕОРЕМА. Якщо  а , то

                               (34) 

Доведення. Інтеграл в правій частині формули (34) носить назву інтеграл Дюамеля.

        По теоремі про множення зображень будемо мати

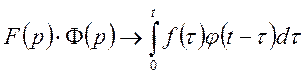
звідки на основі формули (20) можна записати

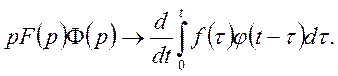
        Застосовуючи до останньої формули правило диференціювання по параметру

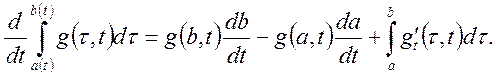
        Отримаємо остаточну формулу

.

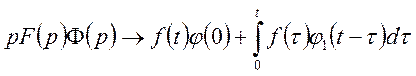        Теорему доведено.

        Приклад. Знайти оригінал для функції

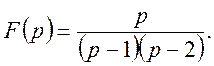
        Маємо

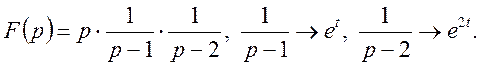
        Використовуючи формулу (34) знаходимо

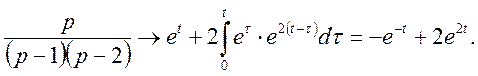
        Вправи. Знайти оригінал для функцій F(p):

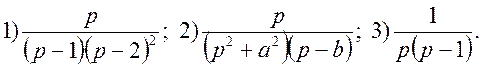
      2.11 Формула обернення

        Означення. Функція f(t) задовольняє на замненому інтервалі  умовам Діріхле, якщо:

        1) f(t) неперервна на  або має на цьому інтервалі скінчене число точок розриву першого роду;

        2) f(t) монотонна на  або має на цьому інтервалі скінчене число екстремумів.

        Таким чином, якщо функція відповідає умовам Діріхле на інтервалі , то цей інтервал можна розділити на скінчене число інтервалів, в кожному з яких f(t) буде неперервна і монотонна.

        ТЕОРЕМА. Якщо функція f(t) задовольняє на будь – якому скінченому інтервалі умовам діріхле і інтеграл

 збігається абсолютно вздовж прямої  то

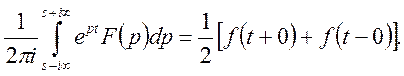                                 (35)

        Доведення цієї теореми виходить за рамки даного підручника і тому не приводиться.

        В точках неперервності функції f(t) можна записати

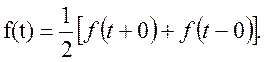
        В наслідок маємо

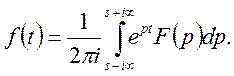                                                              (36)

        Рівність (36) називається формулою обернення Рімана – Меліна і дозволяє знаходити оригінал f(t) по зображенню F(p).

        Безпосереднє використання формул (36) не завжди можливе. Наведемо без доведення теорему, що дозволяє отримувати оригінал f(t) більш простим способом.

        ТЕОРЕМА. Нехай мезоморфна функція F(p) аналітична в півплощині  в довільній площині  рівномірно відносно arg p, а також існує невласний інтеграл 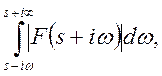   тоді

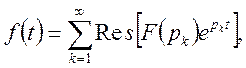                                                                  (37)

де  - полюси функції F(p).

        Практичне використання формули (37) приводить в наступному підрозділі.

      2.12 Формули розкладання

Розглянемо випадок, коли F(p) – раціональна функція:

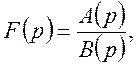
де А(р) і В(р) – багаточлени, причому степінь багаточлена А(р) менше за степінь багаточлена В(р). Нулі багаточлена В(р) будуть полюсами функції F(p) (вважаємо, що А(р) і В(р) не мають спільних коренів). Використовуючи для даного випадку формулу (37), будемо мати