Маємо 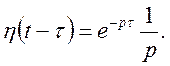
Приклад 2. Знайти зображення функції, поданої на рис. 2.
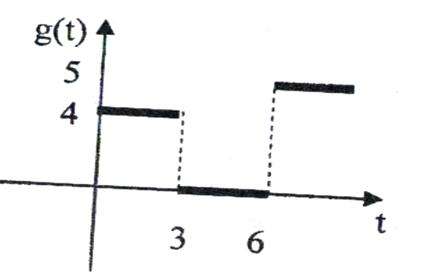
Рис. 2.
Функцію g(t) можна зобразити через узагальнену функцію Хевісада
![]()
Далі, використавши теореми лінійності і запізнення, знаходимо
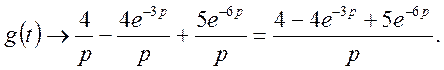
ТЕОРЕМА
2 (випередження). Якщо ![]() і
і ![]() , то
, то
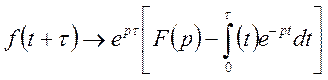 (14)
(14)
Доведення.
Функція ![]() описує фізичний процес, який
починається на τ раніше ніж процес
описує фізичний процес, який
починається на τ раніше ніж процес ![]() .
.
Для доведення
знайдемо зображення функції ![]() :
:
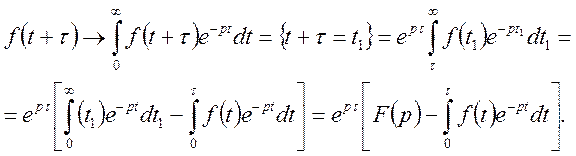
Теорему доведено.
ТЕОРЕМА
3 (зсунення). Якщо ![]() довільне
комплексне число і
довільне
комплексне число і ![]() , тоді
, тоді
![]() (15)
(15)
Доведення. Ця теорема дозволяє знаходити зображення функцій, що затухають з часом по експоненціальному законові.
Маємо
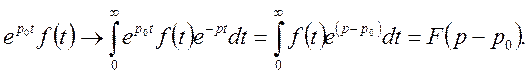
Теорему доведено.
Приклад 3.
Знайти зображення затухаючої функції ![]()
Маємо 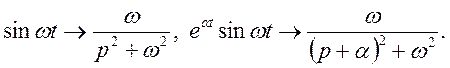
Вправи.
1. Використовуючи теорему запізнення знайти зображення функцій
1) 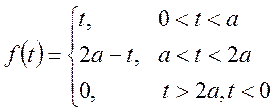
2) 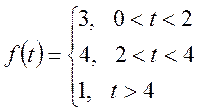
3) 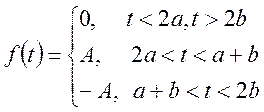
2. Знайти зображення періодичного з періодом Т прямокутного імпульсу f(t) величиною А і тривалості τ (рис. 3).
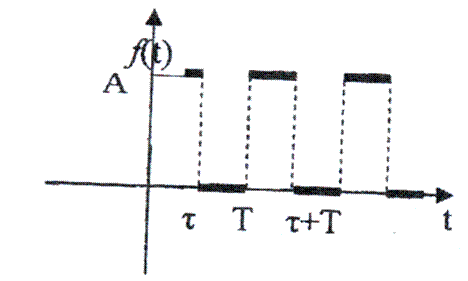
Рис. 3
3. Використовуючи теорему зсунення, знайти зображення функцій
1) ![]()
4) ![]()
2.4 Зображення періодичних оригіналів
Розглянемо періодичний оригінал f(t) з періодом Т, тобто f(t+T)=f(t) для всіх t > 0.
ТЕОРЕМА 1. Зображення періодичного оригіналу f(t) з періодом Т знаходиться по формулі
![]()
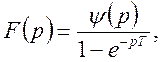 (16)
(16)
де
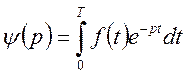 (17)
(17)
Доведення. Будемо мати
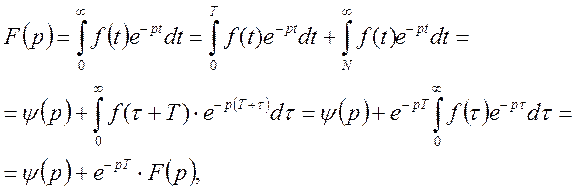
Тобто
![]()
Звідси
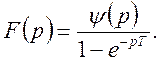
Теорему доведено.
Має місце і зворотна теорема. Її сформулює без доведення.
ТЕОРЕМА 2. Оригінал f(t), зображення якого має вигляд (16), є періодичною функцією з періодом Т, що одержуються шляхом періодичного продовження функції.
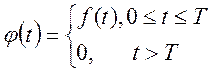
із інтервалу ![]() на числовий інтервал
на числовий інтервал ![]() .
.
Розглянемо деякі приклади.
Приклад 1. Знайти зображення періодичної функції
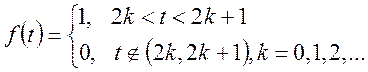
Для розв’язку цього прикладу побудуємо графік функції f(t):
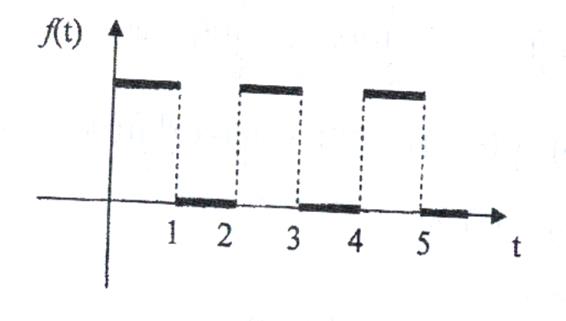
Рис. 4
Таким чином, ми маємо періодичну функцію з періодом Т = 2. Відповідно до формули (16) і (17) знайдемо
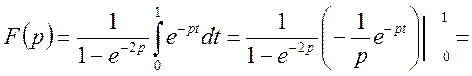
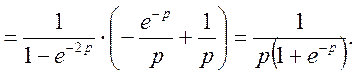
Остаточно
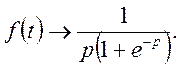
Приклад 2. Використовуючи формули (16), (17), знайти зображення функції f(t)=|sin t|.
Функція |sin t| є періодичною функцією з періодом Т = π і її графік має вигляд
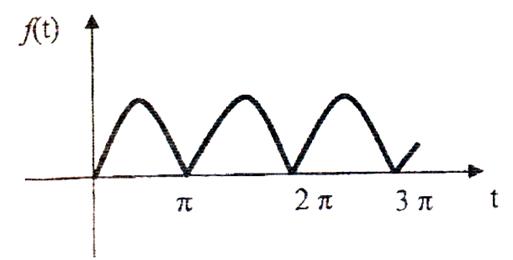
Рис. 5
Для знаходження F(p) застосовуємо формули (16), (17)
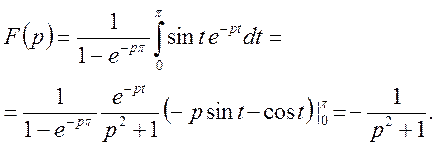
Остаточно

Приклад 3. Знайти оригінал функції f(t) з данним зображенням
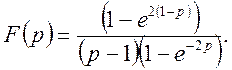
Для знаходження оригіналу f(t) скористаємось зворотною теоремою 2.
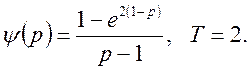
Таким чином
![]()
Графік функції f(t) має вигляд
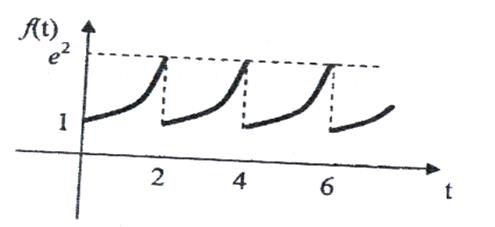
Рис. 6
Вправи.
1. Знайти зображення періодичних функцій:
1) 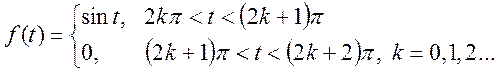
2) 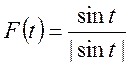
3) ![]()
2. Знайти зображення періодичних функцій, зображених графіками
1) 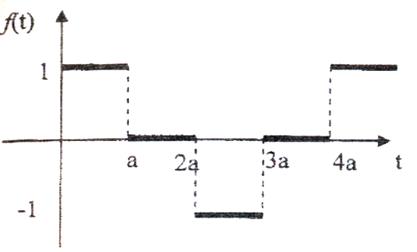
Рис. 7
2) 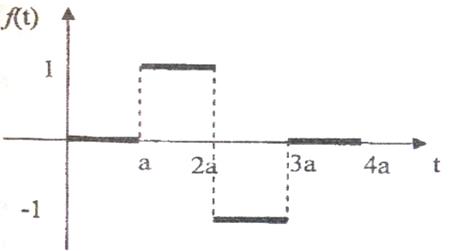
Рис. 8
3) 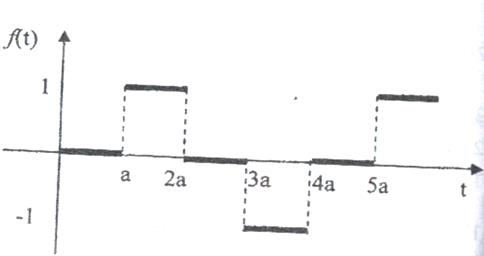
Рис. 9
4) 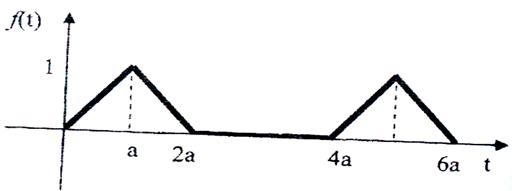
Рис. 10
2. Знайти оригінал по зображенню
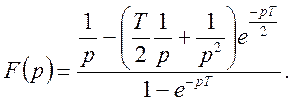
2.5 Теореми диференціювання і інтегрування оригіналу
ТЕОРЕМА
1 (диференціювання оригіналу). Якщо ![]() і функції
і функції ![]() є оригінали, то
є оригінали, то
![]()
де 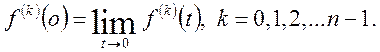
Доведення. Використовуючи формули (2) і інтегрування частинами, знаходимо
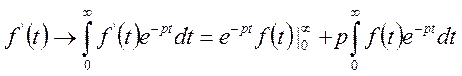
У півплощині ![]() мають місце формули
мають місце формули
![]() ,
,
тому
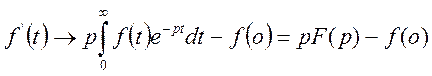 (18)
(18)
Застосуємо формулу (18) до другої похідної
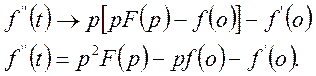 (19)
(19)
Застосовуючи
формулу (18) (n-1) раз до n-ї похідної ![]() будемо
мати
будемо
мати
![]()
Теорему доведено.
З а у в а
ж е н н я 1. У пункті 1.1 було встановлено, що 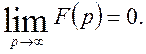 Отже,
якщо
Отже,
якщо ![]() є оригінал, то має місце формула
є оригінал, то має місце формула
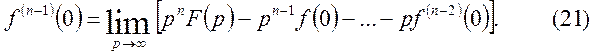
З а у в а
ж е н н я 2. Якщо f(0)=![]()
то
![]() (22)
(22)
Таким чином, у цьому випадку диференціювання оригіналу відповідає множенню зображення на відповідний степінь р.
Приклад 1. Найти зображення виразу
![]()
Застосовуючи формулу (2) будемо мати
![]()
Далі, скориставшись теоремою лінійності зображення, одержуємо відповідь
![]()
ТЕОРЕМА 2 (інтегрування оригіналу). Якщо
![]() то
то
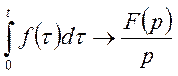 (23)
(23)
Доведення.
Розглянемо функцію 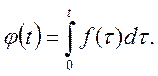 Очевидно, що ця функція
Кусково – неперервна і
Очевидно, що ця функція
Кусково – неперервна і ![]() при t<0.
при t<0.
Крім того,
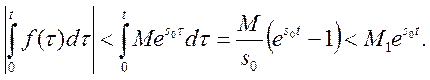
Отже, функція
![]() є оригінал. Причому
є оригінал. Причому ![]() . Хай
. Хай ![]() Звідси
по теоремі диференціювання оригіналу маємо
Звідси
по теоремі диференціювання оригіналу маємо
![]()
або
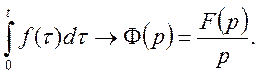
Теорему доведено.
З а у в а ж е н н я. Таким чином, операції інтегрування оригіналу відповідає поділ зображення на величину р.
Приклад 2. Знайти зображення функції
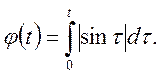
Скориставшись прикладом 2 пункту 2.4 маємо

![]() Далі, застосувавши до останньої
формули теорему про інтегрування оригіналу, одержуємо
Далі, застосувавши до останньої
формули теорему про інтегрування оригіналу, одержуємо
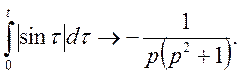
Вправи. Знайти зображення для диференційних виразів:
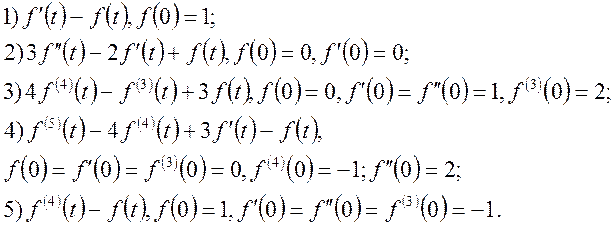
2.6 Диференціювання і інтегрування зображення
ТЕОРЕМА
1. Якщо ![]() то
то
![]() (24)
(24)
Доведення.
У пункті 2.1 було показано, що зображення F(p) є аналітична
функція в області ![]() і має місце формула (7)
і має місце формула (7)
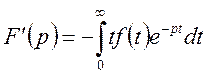
Застосовуючи цю формулу (n-1) разів будемо мати
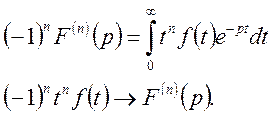
або
Теорему доведено.
Приклад 1. Знайти зображення функцій:
![]()
Маємо
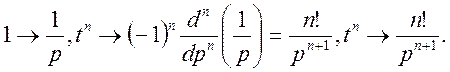
2) f(t)=t sin t.
Скористаємося формулою 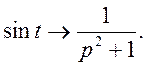
Будемо мати
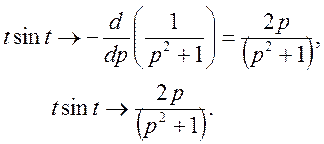
ТЕОРЕМА
2. Якщо функція 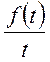 є оригінал і
є оригінал і
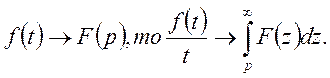
Доведення.
Нехай 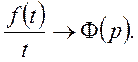 Звідси, по теоремі 1 цього пункту
Звідси, по теоремі 1 цього пункту ![]()
Про інтегруємо останню рівність в межах від p до q:
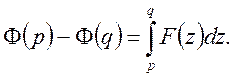
Відомо, що ![]() при
при ![]() Тому
Тому
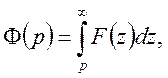
або 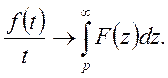
Теорему доведено.
Приклад 2. Знайти зображення
функції 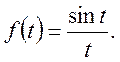
Так як, 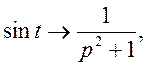 то
то
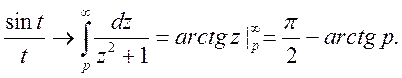
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.