


















































3.8 Векторний добуток векторів
та його властивості
Означення. Векторним добутком двох векторів ![]() і
і ![]() називається
такий вектор
називається
такий вектор ![]() , який:
, який:
1.
Має модуль 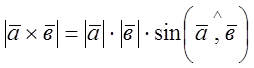 , де
, де 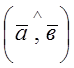 - кут між векторами
- кут між векторами ![]() і
і
![]()
2.
Перпендикулярний до
кожного з векторів, тобто ![]() ,
, ![]()
3.
Має напрямок такий, щоб
трійка векторів ![]() ,
, ![]() і
і
![]() була правою, тобто напрямок, який
знаходиться за правилом правої руки.
була правою, тобто напрямок, який
знаходиться за правилом правої руки.
Механічний зміст векторного
добутку полягає в обчисленні моменту ![]() вектора сили
вектора сили ![]() , прикладеного в точці відносно нерухомо
закріпленої точки А (рис. 11), тобто
, прикладеного в точці відносно нерухомо
закріпленої точки А (рис. 11), тобто
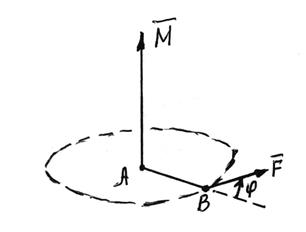
![]() , а величина моменту обчислюється за
формулою
, а величина моменту обчислюється за
формулою ![]() . Геометричний зміст векторного добутку
векторів
. Геометричний зміст векторного добутку
векторів ![]() і
і ![]() полягає
в тому, що його модуль
полягає
в тому, що його модуль ![]() численно
дорівнює площині паралелограма, побудованого на цих векто
численно
дорівнює площині паралелограма, побудованого на цих векто рах,
тобто
рах,
тобто
![]()
![]() =
=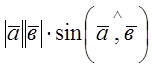 .
.
Властивості векторного добутку (без доведення)
1. ![]() - (антикомутативна, антисиметрична).
- (антикомутативна, антисиметрична).
2. ![]() (нільпотентна), наслідком її є
(нільпотентна), наслідком її є ![]() .
.
3. ![]() - (асоціативна відносно скалярного
множника).
- (асоціативна відносно скалярного
множника).
4. ![]() - (білінейна, або дистрибутивна).
- (білінейна, або дистрибутивна).
5. ![]() тобто умова колінеарності векторів.
тобто умова колінеарності векторів.
6. Для правої
трійки координатних ортів маємо ![]()
![]()
![]() , тощо.
, тощо.
7. Для подвійного векторного добутку виконується тотожність Якобі (правило ВАС - САВ)
![]()
8. Нехай задано
два вектори в декартовій системі координат ОХУZ: ![]() і
і
![]() . Тоді за властивостями векторного
добутку отримаємо
. Тоді за властивостями векторного
добутку отримаємо
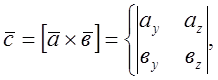
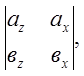
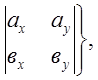 або
або
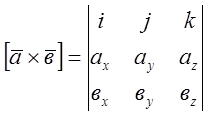
Приклад. ТочкаА (4, -1, 3) твердого тіла
закріплена, а в точці його В(0, 3, 5) прикладена сила ![]() .
.
Знайти момент сили ![]() відносно
точки А.
відносно
точки А.
Розв’язання .
Вектор ![]() має координати
має координати ![]() . Обертальний момент
. Обертальний момент ![]()
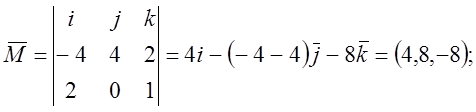
Величина моменту ![]()
![]()
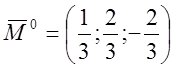 - одиничний
вектор моменту.
- одиничний
вектор моменту.
3.9 Мішаний добуток трьох векторів та його
геометричний зміст
Означення. Мішаним добутком трьох векторів ![]() ,
, ![]() і
і
![]() називається скалярний добуток
векторного добутку двох перших векторів
називається скалярний добуток
векторного добутку двох перших векторів ![]() і
і
![]() та третій вектор
та третій вектор ![]() , тобто
, тобто ![]() .
.
Теорема. Мішаний добуток трьох векторів ![]() ,
, ![]() і
і
![]() дорівнює об’єму паралелепіпеда,
побудованого на цих векторах, зі знаком "плюс", якщо вектори
дорівнює об’єму паралелепіпеда,
побудованого на цих векторах, зі знаком "плюс", якщо вектори ![]() ,
, ![]() і
і
![]() утворюють праву трійку векторів, і
зі знаком "мінус", якщо ця трійка – ліва. Якщо вектори
утворюють праву трійку векторів, і
зі знаком "мінус", якщо ця трійка – ліва. Якщо вектори ![]() ,
, ![]() і
і
![]() компланарні, то їх мішаний добуток
дорівнює нульові, тобто
компланарні, то їх мішаний добуток
дорівнює нульові, тобто ![]() 0 – необхідна і достатня умова компланарності
трьох векторів, це є геометричний зміст мішаного добутку.
0 – необхідна і достатня умова компланарності
трьох векторів, це є геометричний зміст мішаного добутку.
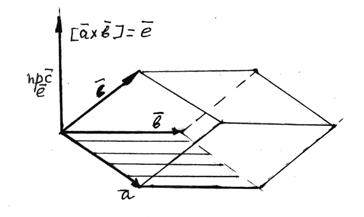
![]()
![]() V = S · H, S =
V = S · H, S = ![]()
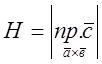 , оскільки
, оскільки ![]()
![]()
Таким чином,
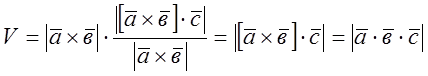
Властивості мішаногодобутку векторів
1. ![]()
2. ![]()
![]()
3.
Нехай задано три вектори
координатами ![]() ,
, ![]() і
і
![]() , тоді
, тоді
![]()
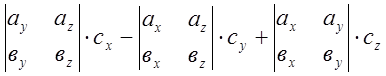 , або
, або 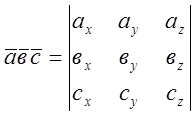
Наслідок 1. Об’єм піраміди, побудованої на векторах ![]() ,
, ![]() і
і
![]() можна записати у вигляді
можна записати у вигляді
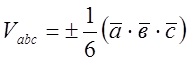
Наслідок 2. Необхідною і достатньою умовою компланарності трьох векторів
![]() ,
, ![]() і
і
![]() в координатній формі є
в координатній формі є
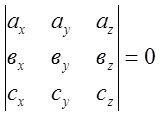
Приклади. Нехай задано три вектори ![]()
![]()
![]() .
.
1.
Знайти кут між
двома векторами ![]() і
і ![]() .
.
Розв’язання .
Кут між двома векторами ![]() і
і ![]() знайдемо за формулами
знайдемо за формулами
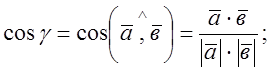
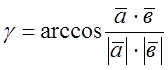
Відповідь: 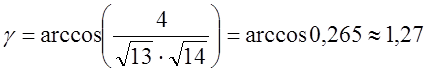 (радіан).
(радіан).
2.
Визначити площу ![]() паралелограма, побудованого на векторах
паралелограма, побудованого на векторах
![]() і
і ![]() .
.
Розв’язання.
Площу паралелограма ![]() знайдемо за
формулами
знайдемо за
формулами
а) 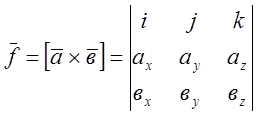 б)
б) ![]()
Відповідь: а) ![]() б)
б) ![]() (кв.
ед.)
(кв.
ед.)
3.
Обчислити довжини
діагоналей d1
і d2 паралелограма, побудованого на векторах ![]() і
і ![]() .
.
Розв’язання.
Довжини діагоналей d1 і d2 паралелограма знайдемо за формулами
а) ![]()
![]() ,
тобто
,
тобто 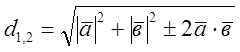
б) або за формулами
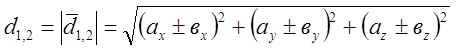
Відповідь: 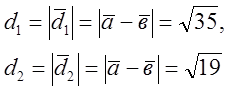
4.
Знайти проекцію
вектора ![]() на вектор
на вектор ![]() .
.
Розв’язання.
Проекцію вектора ![]() на
вектор
на
вектор ![]() знайдемо за формулою
знайдемо за формулою 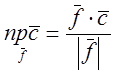 .
.
Відповідь: 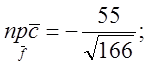
5. Обчислити об’єм ![]() паралелепіпеда, побудованого на векторах
паралелепіпеда, побудованого на векторах
![]() ,
, ![]() і
і
![]() .
.
Розв’язання.
![]() , де
, де 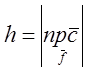 і
відповіді задач 2 і 4. Тобто
і
відповіді задач 2 і 4. Тобто 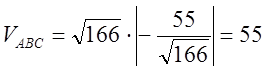
Відповідь: ![]() (куб. ед.)
(куб. ед.)
6.
Знайти мішаний
добуток ![]() трьох векторів
трьох векторів ![]() ,
, ![]() і
і
![]() .
.
Розв’язання.
Маємо 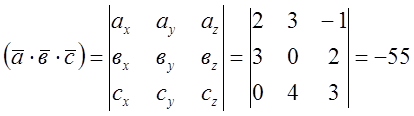
Відповідь: ![]() = -55.
= -55.
Зауваження. Абсолютна величина числа ![]() - об’єм паралелепіпеда,
побудованого на векторах
- об’єм паралелепіпеда,
побудованого на векторах ![]() ,
, ![]() і
і ![]() ,
тобто
,
тобто ![]() (куб. ед.)
(куб. ед.)
3.10 Запитання для самоперевірки
1. Дайте означення визначника n-го порядку.
Сформулюйте властивості визначників.
2. Сформулюйте теорему Крамера (сумісності і визначеності системи лінійних алгебраїчних рівнянь - СЛАР).
3. Що ви знаєте про метод послідовних вилучень невідомих?
4. У чому полягає прямий та обернений хід методу Гаусса?
5. Які два вектори називають колінеарними, рівними?
Що ви знаєте про базис на площині?
6. Дайте означення суми двох векторів.
Сформулюйте правило трикутника, многокутника.
7. Назвіть лінійні операції над векторами та сформулюйте алгебраїчні властивості лінійних операцій.
8. Дайте означення проекції вектора на вісь та сформулюйте властивості проекцій вектора на вісь.
9. Що називається скалярним добутком двох векторів?
Які властивості має скалярний добуток?
10. Дайте означення векторного добутку і сформулюйте властивості векторного добутку.
11. У чому полягає механічний зміст скалярного добутку та векторного добутку?
12. Дайте означення мішаного добутку трьох векторів і сформулюйте теорему, яка виражає геометричний зміст мішаного добутку.
13. Дайте означення компланарності трьох векторів. Запишіть умову компланарності векторів в координатній формі.
14. Що ви знаєте про базис в просторі R3?
Що ви знаєте про декартів базис?
3.11 Завдання для самостійної роботи
Зміст роботи
3.1. а) Розв’язати СЛАР за формулами Крамера;
б) Перевірити знайдений розв’язок системи
в) Розв’язати цю систему методом Гаусса.
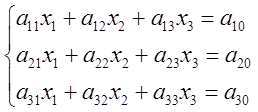
ВАРІАНТИ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.