Векторний добуток векторів та його властивості. Аналітична геометрія в просторі та на площині (Теоретичний матеріал та контрольні завдання зі зразками вирішення з вищої математики), страница 3

№№ п/п	а			в			с
	ах	ау	аz	вх	ву	вz	сх	су	сz
3.01	4	5	0	1	7	-2	9	2	4
3.02	3	4	2	8	2	-1	-3	-1	1
3.03	2	-1	1	0	3	-2	-5	1	1
3.04	2	1	2	1	-4	3	1	2	2
3.05	1	-5	2	1	2	2	-4	3	1
3.06	2	-1	1	-4	3	1	-1	-1	4
3.07	4	-3	2	9	2	5	-3	4	5
3.08	1	1	-1	1	8	3	-6	2	-4
3.09	1	2	3	5	2	-1	-1	1	1
3.10	1	2	4	31	5	1	2	29	3
3.11	1	3	-1	1	2	-5	2	2	3
3.12	3	-1	2	3	5	2	1	-3	1
3.13	1	-5	3	-2	2	7	-1	3	4
3.14	2	-1	1	2	3	2	-2	-1	1
3.15	2	-1	4	3	1	2	5	-3	5
3.16	3	2	1	0	1	3	4	6	1
3.17	5	-1	2	1	3	1	-1	0	1
3.18	4	-5	2	-4	2	1	-1	2	1
3.19	-1	2	-5	1	3	5	1	8	2
3.20	3	1	-5	3	5	-2	7	5	2
3.21	1	2	-3	0	2	-1	4	5	3
3.22	4	-2	3	1	2	-1	4	3	1
3.23	1	2	3	4	2	4	6	3	3
3.24	0	1	5	0	1	-4	-4	0	1
3.25	3	2	1	-1	5	2	-1	1	6
3.26	3	2	4	8	2	4	4	-5	11

ГЛАВА IV. АНАЛІТИЧНА ГЕОМЕТРІЯ В ПРОСТОРІ ТА НА ПЛОЩИНІ

Аналітична геометрія – розділ математики, в якому геометричні задачі розв’язуються за допомогою формул (аналізу) на основі методу координат і введення довільної (змінної) точки об’єкту.

4.1 Загальні поняття і означення.

Найпростіші задачі аналітичної геометрії

Означення 1. Рівняння F(x, y, z) = 0 називається рівнянням даної поверхні в декартовій системі координат простору ОХYZ (R³), якщо координати всіх точок М(x, y, z), що належать даній поверхні, задовольняють цьому рівнянню і не задовольняють координати жодної точки, що не належить даній поверхні d, і позначається

d: F(x, y, z) = 0        (1)

Будь-яка лінія L у просторі задається системою двох рівнянь з трьома змінними, тобто у вигляді:

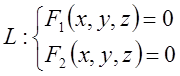    (2)

і розглядається як лінія перетину двох поверхонь.

Означення 2. Рівняння F(х, у) = 0 називається рівнянням даної лінії в декартовій системі координат на площині ОХУ (R²), якщо координати всіх точок  М(х, у), що належать даній лінії, задовольняють цьому рівнянню і не задовольняють координати жодної точки, що не належить даній лінії L, і позначається

L:F(x, y) = 0   (3)

Означення 3. Рівняння  F(x, y) = 0в декартовій системі координат простору ОХYZ визначає поверхню d, яка називається циліндром з напрямною лінією

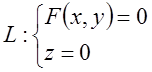   (4)

й твірною, паралельною до осі OZ.

Наприклад, рівняння сфери, центр якої знаходиться в точці С (0, 1, -3), а радіус дорівнює R = 5, має вигляд в декартовій системі координат простору ОХУZ:

d: x² + (y - 1)² + (z + 3)² = 25

Рівняння лінії перетину цієї сфери з координатною площиною ОХУ має вигляд:

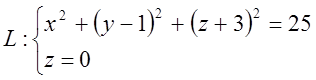
Тобто ця система рівнянь визначає коло, яке лежить в площині ОХУ з центром, в точці С₁ (0, 1, 0) і радіусом R₁ = 4 й рівняння        х² + (у - 1)² = 16 в аналітичної геометрії на площині (R²) визначає це коло, але в аналітичної геометрії простору (R³) теж саме визначає круговий циліндр з напрямною лінією

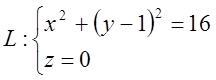
й твірною, паралельною до осі OZ.

Найпростіші задачі аналітичної геометрії

1.  Перетворення декартових координат при паралельному зсуві.

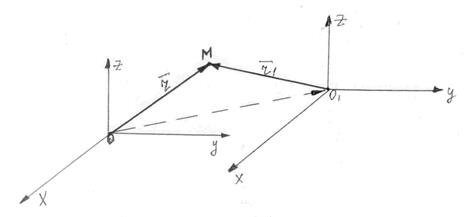
Нехай в просторі дано дві декартові паралельні системи координат з початком О і О₁, причому точка О (х₀, у₀, z₀) має координати відносно старої системи координат ОХУZі відповідні їх ох і ОХ, оу і ОУ, oz і OZ мають однакові напрями (рис. 12)

		Рисунок 12

 

Нехай довільна точка М розглядається в обох системах охуz і ОХУZ, тобто радіус – вектор , радіус-вектор , радіус-вектор . Тоді маємо векторні рівності:

  або   (рис. 12).

Тобто 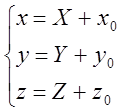  (1),   або  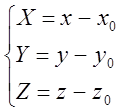 (2)

Формули (1) виражають старі координати точки М через нові координати. І навпаки, формули (2) виражають нові координати точки М через старі. Тобто формули (1) і (2) виражають співвідношення між новими та старими координатами точки М при паралельному зсуві декартової системи координат в просторі.