Векторний добуток векторів та його властивості. Аналітична геометрія в просторі та на площині (Теоретичний матеріал та контрольні завдання зі зразками вирішення з вищої математики), страница 4

2.  Відстань між двома точками М₁ і М₂.

Нехай дано М₁(х₁, у₁, z₁) та М₂(х₂, у₂, z₂). Треба знайти            d = М₁М₂.

Оскільки вектор 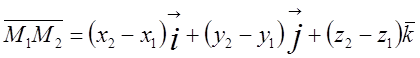, то модуль, або довжина цього вектора дорівнює

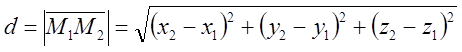
Таким чином, відстань між двома точками дорівнює кореню квадратному з суми квадратів різниць відповідних координат цих точок.

3.  Ділення відрізку в даному відношенні.

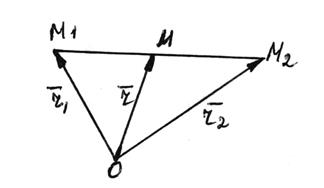
 Точка М поділяє відрізок М₁М₂ у відношенні l, якщо

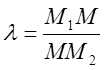  (1)

Нехай точки М₁(х₁, у₁, z₁), М₂(х₂, у₂, z₂) і l - відомі.

Треба знайти координати точки М(х, у, z).

Рисунок 13

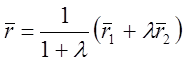Оскільки ,  , , то маємо векторну рівність  звідси   (2),  тобто у координатній формі

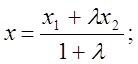
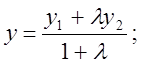
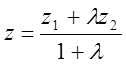      (3)

де l¹ -1. Якщо l> 0, то точка М міститься між точками М₁ і М₂. Якщо l = 1, то точка М – середина відрізка М₁М₂ і тоді

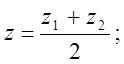     (4)

Якщо l< 0, то точка М міститься зовні відрізка М₁М₂.

4.2 Рівняння площини в просторі R³

Теорема. Будь-яка площина p в просторі описується рівнянням першого степеня відносно змінних х, у, z, тобто

p: Ах + Ву + Сz + D = 0  (1), де А, В, С, DÎR.

 - нормальний вектор площини p, або вектор нормалі до площини .

Рівняння (1) називають загальним рівнянням площини.

Справедливе й протилежне твердження.

Обернена теорема. Будь-якому рівнянню першого степеня (1) відносно змінних х, у, z відповідає площина (і лише площина) в просторі R³.

Рівняння (1) еквівалентне рівнянню

p: А(х – х₀) + В(у – у₀) + С(z – z₀) = 0  (2),

де , М – довільна точка площини. Це рівняння визначає площину p, що проходить через фіксовану точку М₀(х₀, у₀, z₀) перпендикулярно заданому вектору .

Якщо задані три точки М₁(х₁, у₁, z₁), М₂(х₂, у₂, z₂),            М₃(х₃, у₃, z₃), що не лежать на одній прямій, то рівняння площини, яка проходить через три задані точки, можна записати у вигляді:

      

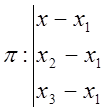
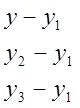
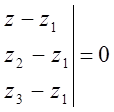
Розташування площини в просторі

1.  Нехай в рівнянні (1) D = 0, тоді площина проходить через початок координат О(0, 0, 0).

2.  Нехай А = 0, тоді площина p паралельна осі ОХ ()

3.  Нехай А = В = 0, тоді площина p перпендикулярна осі ОZ ( або ).

4.  Припустимо, що D ¹ 0, тоді рівняння (1) можна записати у вигляді:

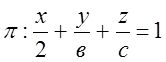 (4),

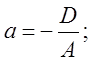
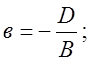
де   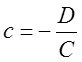     - відрізки, які площина відтинає від координатних осей, тобто проходить через точки М₁(а, 0, 0),          М₂(0, в, 0), М₃(0, 0, с).

Рівняння (4) називають рівнянням площини у відрізках.

Відстань від точки М^*(х^*, у^*, z^*) до площини p

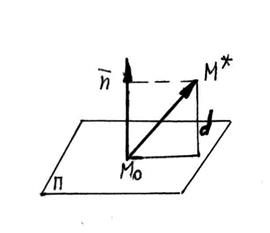Нехай в просторі задано площину p рівнянням (2) і точку М^*, яка не належить площині. Проведемо нормаль  до площини p й позначимо точку її перетину з площиною через М₀. Тоді довжина перпендикуляра, опущеного із точки М^* до площини p, називається

	Рисунок 14

 

відстанню від точки до площини (рис. 14) позначається

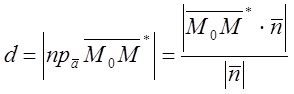  , або

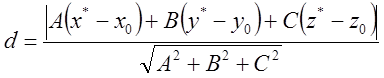  (5)

Таким чином, відстань точки М^* до площини p можна обчислювати також за формулою

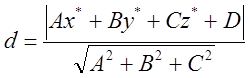  (6)

Кут між двома площинами

Кут визначається як кут між двома векторами  і , перпендикулярними до даних площин і приведеними до спільного початку. Цей кут можна обчислити за допомогою скалярного добутку векторів, тобто:

,    

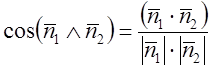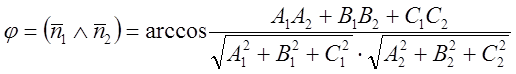
 Звідси випливає умова взаємної перпендикулярності двох площин тобто

А₁А₂ + В₁В₂ + С₁С₂ = 0

Умова взаємної паралельності двох площин випливає з умови колінеарності їх нормальних векторів (), тобто

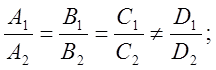
Приклад. Знайти рівняння площини, що проходить через точки М₁(1, 2, 1), М₂(0, 3, -1) паралельно до осі ОУ.

Розв’язання.

Шукаємо рівняння площини у вигляді Ах + Сz + D = 0.

Підставивши в це рівняння координати точок М₁ і М₂, одержимо систему двох рівнянь з трьома змінними А, В, і D, тобто

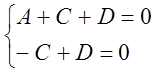
Система невизначена, тобто має нескінчену множину розв’язків: С= D, А = -2D, де  D¹ 0 параметр, через який визначаються коефіцієнти рівняння площини А, С, і D. Таким чином, підставивши їх в рівняння площини, маємо:

-2Dx + Dz + D = 0  або

-D(2x – z - 1) = 0

остаточно: Р: 2х – z – 1 = 0.

4.3 Рівняння прямої в декартовій прямокутній

системі простору ОХУZ (R³)

Пряму L в просторі можна задати декількома способами, а саме:

1.  Розглядати її як лінію перетину двох непаралельних площин , тобто системою двох лінійних рівнянь p₁ і p₂

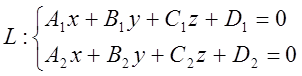  (1),

які описують цю лінію L й називаються загальними рівняннями прямої в просторі.

Наприклад, 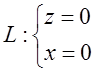  -  вісь ОУ,

як лінія перетину координатних площин ОХУ то ОУZ.

2.  За допомогою фіксованої точки М₀, яка лежить на прямій    (М₀ ÎL) та ненульового вектора , який лежить на даній прямій L або їй паралельній  і називається напрямним вектором даної прямої. Дійсно, якщо М(х, у, z) довільна точка прямої L, то і  колінеарні при будь-якому положенні точки М на прямій L, тобто   (2).

Лінійне векторне рівняння (2) еквівалентне трьом скалярним рівнянням виду:

х – х₀ = tm, y – y₀ = tn, z – z₀ = tp, або

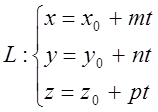 (3)

які називаються параметричними рівняннями прямої в просторі.

Умову колінеарності двох векторів (2) можна записати в координатній формі у вигляду

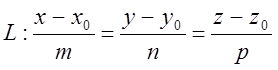 (4)

Ці рівняння називаються канонічними рівняннями прямої в просторі.

3.  Пряму в просторі можна задати двома фіксованими точками:

М₁(х₁, у₁, z₁) ÎL і М₂(х₂, у₂, z₂) ÎL.

Оскільки , то взявши вектор  за напрямний  для L, з (4) дістанемо

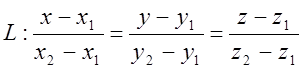 (5) – рівняння прямої, яка проходить через дві задані точки у просторі.

Розташування прямої в просторі

1.  Якщо пряма L проходить через точку М₀(х₀, у₀, z₀) і паралельна координатної площині ОХУ, то її рівняння має вигляд

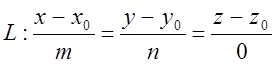, де  (6)

2.  Якщо пряма L проходить через точку М₀(х₀, у₀, z₀) і паралельна, наприклад, осі ОУ, то її рівняння має вигляд:

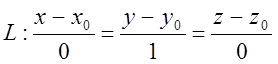, де  (7)

Рівняння осі ОУ можна записати в канонічному вигляді

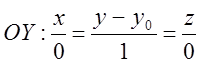 , де у₀ ÎR, або в загальному вигляді

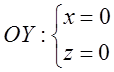, тобто

як рівняння лінії перетину двох координатних площин OYZ та ОХУ.

Кут між двома прямими

Кут між двома прямими L₁ і L₂  в просторі, заданими їх канонічними рівняннями, визначається як кут між напрямними векторами  і . Згідно з формулою скалярного добутку векторів і , дістанемо