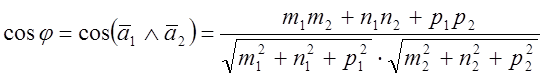Векторний добуток векторів та його властивості. Аналітична геометрія в просторі та на площині (Теоретичний матеріал та контрольні завдання зі зразками вирішення з вищої математики), страница 5

 (8)

Звідси випливає умова взаємної перпендикулярності прямих L₁ і L₂.

m₁m₂ + n₁n₂ + p₁p₂ = 0  (9)

Якщо прямі L₁ і L₂ паралельні, то напрямні вектори і  цих прямих колінеарні , тобто

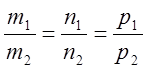 (10)

4.4  Взаємне розташування прямої

        та площини у просторі

З рівнянь площини Р:Ах + Ву + + Сz + D = 0 і прямої

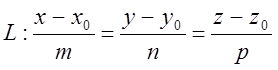, де М₀   ÎL.

Маємо  - нормальний вектор площини Р.

 - напрямний вектор прямої L, точка М₀(х₀, у₀, z₀) – точка перетину прямої і площини і L₁ – проекція прямої L на площину Р.

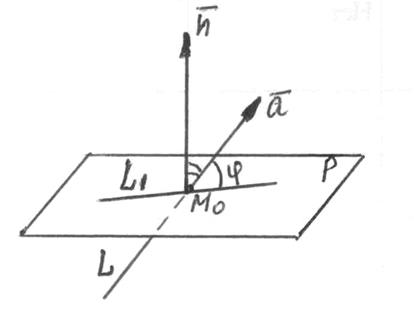
Означення. Кутом між прямою L і площиною Р називається кут j між прямою і її проекцією на цю площину. Можна знайти додатковий кут 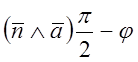за формулою

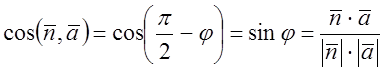 (1),

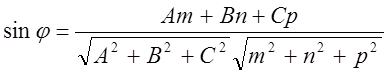тобто  (2)

Умова взаємної паралельності прямої L і площини Р рівнозначна умові , тобто Am + Bn + Cp = 0 (3)

Умова взаємної перпендикулярності прямої L і площини Р рівнозначна умові , а тому маємо

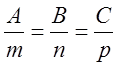  (4)

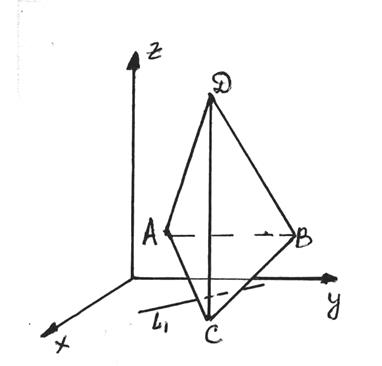
Приклади. Дано чотири вершини тетраедра АВСD   А(3, 2, 3), В(0, 8, 2), С(4, 6, -1), D(1, 5, 10) (мал.15)

1.  Скласти рівняння площини, що проходить через ребро АВ і паралельна до осі ОУ.

Розв’язання.

 

Вісь , вектор . Вектор, перпендикулярний до шуканої площини, дорівнює

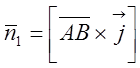, тобто

Рисунок 15

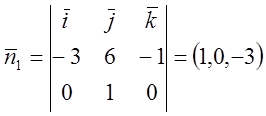
Отже рівняння площини Р₁

1.

Р₁: х – 3z + 6 = 0

2.  Скласти рівняння площини, яка проходить через точки     А, В, С.

Розв’язання.

Згідно з умовою компланарності трьох векторів маємо

, де   .

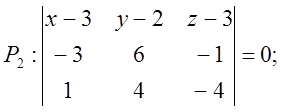 -20(х - 3) – 13(у - 2) – 18(z - 3) = 0,

Р₂: 20х + 13у + 18z – 140 = 0

3.  Знайти відстань точки D до площини АВС (Р₂).

Розв’язання.

Відомо, що 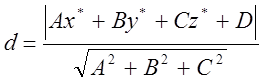, (див. 4.2, ф.(6)), тобто

.

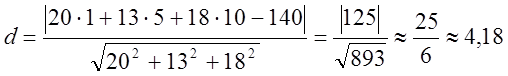4.  Знайти кут між площинами АВС і ОХУ.

Розв’язання.

Нормальний вектор  площини АВС дорівнює , а  координатної площини .

.

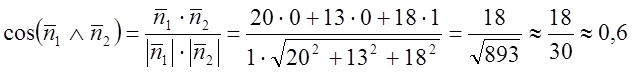
5.  Знайти лінію перетину площини АВС (Р₂) з координатною площиною ОХУ.

Розв’язання.

Загальні рівняння прямої L₁ можна записати у вигляді

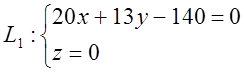
Зробивши тотожні перетворювання, можна записати канонічні рівняння прямої

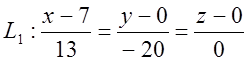
6.  Скласти рівняння площини, якщо точки А і В симетричні відносно неї.

Розв’язання.

Знайдемо вектор . Координати точки N, яка поділяє відрізок АВ навпіл, дорівнюють

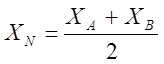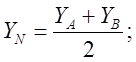
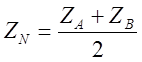;   , тобто

.

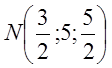Отже, рівняння площини Р₃:

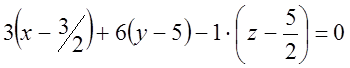
Р₃: 3х – 6у + z + 23 = 0

7.  Скласти рівняння прямої, що проходить через точки А і В та знайти координати її напрямного вектора .

Розв’язання.

Вектор  одночасно є напрямним  вектором  прямої L₁, , тобто

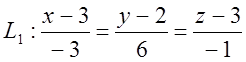  (L₁ = АВ)

8.  Скласти рівняння прямої, яка проходить через точку D і паралельна до прямої АВ.

Розв’язання.

Вектор   також є напрямним вектором  прямої L₂, яка проходить через точку D.

Отже, рівняння прямої з = (-3, 6, -1)

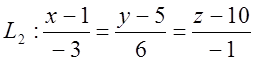
9.  Скласти рівняння прямої L₃, що проходить через точку D та перпендикулярна до площини АВС.

Розв’язання.

Нормальний вектор  площини АВС одночасно є напрямним вектором  прямої , що перпендикулярна до цієї площини, тобто

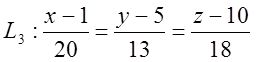
10. Знайти проекцію точки D на площину АВС.

Розв’язання.

Запишемо параметричні рівняння прямої L₃ у вигляді

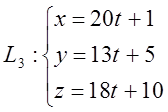
та підставимо їх в рівняння площини АВС.

Р₂: 20х + 13у + 18z – 140 = 0.

Одержимо , тобто

.

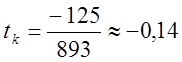Тепер знайдемо проекцію точки D на площину АВС, або координати точки к. Підставивши параметр t_к в рівняння прямої L₃, маємо

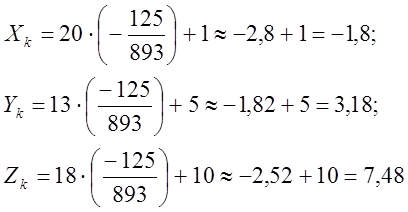
тобто .

11. Знайти кут між ребром СDі граню АВС тетраедра АВСD.

Розв’язання.

Відомо, що кут між прямою і площиною можна знайти за формулою

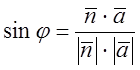, (див. x 4 ф.(1)),

тобто у нашому випадку

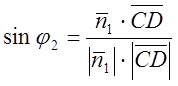 , де

, або  

Таким чином,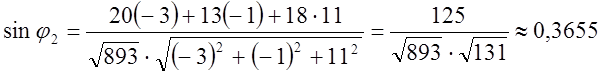

Зробимо перевірку. Для цього знайдемо кут між ребром  і координатною площиною ОХУ за формулою

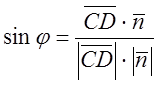, де   

                              

тобто  

З другого боку, цей кут має дорівнювати сумі кутів

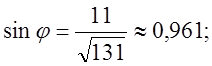
 (див. пр. 4 і пр. 11). Тобто  (в радіанах), або .

4.5 Рівняння прямої на площині

Означення 1. Рівняння F(х, у) = 0 називається рівнянням даної лінії в декартовій системі координат на площині ОХУ(R²), якщо координати всіх точок М(х, у), що належать даній лінії, задовольняють цьому рівнянню і не задовольняють координати жодної точки, що не належать даній лінії L, і позначається

L: F(х, у) = 0 (1)

Будь-яка точка на площині задається системою двох рівнянь з двома змінними, тобто у вигляді

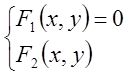  (2)

і розглядається як лінія перетину двох ліній.

Найпростішою лінією є пряма.

Теорема. Між множиною всіх прямих на площині ОХУ і множиною всіх рівнянь першого степеня з двома невідомими існує взаємно однозначна відповідь.

Доведення.

Нехай на площині задана пряма L. Візьмемо на прямій L точку М₀(х₀, у₀) (М₀ ÎL), а на площині вектор , перпендикулярний до . Позначимо змінну точку прямої L через М(х, у) і побудуємо вектор . Скориставшись ознакою перпендикулярності векторів, дістанемо , або в скалярній формі А(х - х₀) + В(у – у₀) = 0 (3),

тобто рівняння прямої, яка проходить через точку М₀(х₀, у₀) і перпендикулярна вектору   .

Позначивши через С = - Ах₀ – Ву₀, маємо рівняння

Ах + Ву + С = 0 (4),

яке називається загальним рівнянням прямої на площині.

Дослідимо рівняння (4):

1)  при С = 0 рівняння (4) має вид Ах + Ву = 0, тобто рівняння прямої, яка проходить через початок координат О(0, 0).

2)  При В = 0 рівняння (4) набирає виду

Ах + С = 0, або х = а, де 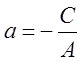  - рівняння прямої, паралельної осі ОУ.

3)  при В = 0 і С = 0 маємо, що х = 0 – рівняння осі ОУ.

4)  якщо А = 0, або А = 0 і С = 0, то матимемо вигадки, аналогічні пп. 2) у = в, де 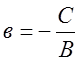  і 3) у = 0 (ось ОХ).

5)  якщо В ¹ 0, то дістанемо рівняння прямої з кутовим коефіцієнтом у = кх + в (5), де 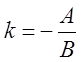 - кутовий коефіцієнт, або тангенс кута між прямою і віссю ОХ. Слід також знати і такі рівняння прямої:

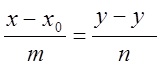  (6) – рівняння прямої, яка проходить через точку

М₀(х₀, у₀) і паралельна вектору , який називається напрямним вектором даної прямої .

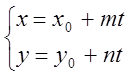 (7) – параметричні рівняння прямої L на площині.

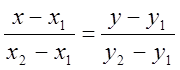  (8) – рівняння прямої, яка проходить через дві точки