Якщо систему координат вибрати так, щоб вісь ОХ
проходила через фокус F перпендикулярно до директриси, то координати
фокуса можна записати у вигляді 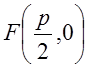 , а рівняння
директриси – у вигляді
, а рівняння
директриси – у вигляді 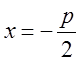 , де р –
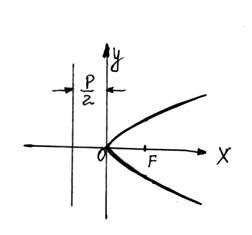
відстань від фокуса до директриси, яка називається параметром параболи. Таким
чином, у цьому випадку канонічне рівняння параболи має вигляд
, де р –
відстань від фокуса до директриси, яка називається параметром параболи. Таким
чином, у цьому випадку канонічне рівняння параболи має вигляд
у2 = 2рх (10) (див. рис. 19)
 |
|||||
 |
 |
||||
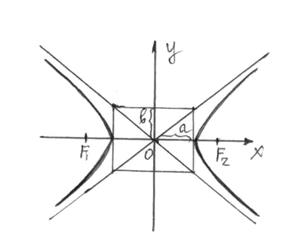
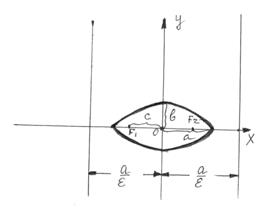
Рисунок 17 Рисунок 18 Рисунок19
Теорема. Якщо r – відстань від
довільної точки кривої другого порядку до якого-небудь фокуса (MF), d – відстань від тієї ж точки до відповідної цьому фокусу директриси (МК),
то відношення ![]() є стала величина, що
дорівнює ексцентриситету кривої, тобто
є стала величина, що
дорівнює ексцентриситету кривої, тобто
 (11)
(11)
При цьому 1) якщо Е < 1, то крива є еліпс,
2) якщо Е > 1, то крива є гіпербола,
3) якщо Е = 1, то крива – парабола.
Приклад. Дано рівняння кривої другого порядку
![]()
1. Звести до канонічного вигляду рівняння кривої другого порядку.
2. Відшукати формули перетворення координат від старої системи ОХУ до нової системи О1ХУ.
3. Знайти координати центра кривої в старій системі та визначити назву цієї кривої.
4. Визначити форму та розміщення лінії другого порядку в декартовій системі координат на площині ОХУ.
5. Знайти ексцентриситет та рівняння директрис і асимптот (якщо вони є).
6. Побудувати криву 2го порядку у старій системі координат ОХУ.
Розв’язання.
1. Виділимо повні квадрати змінних Х та У в лівій частині даного рівняння.
2(х2 – 2х) + 3(у2 + 4у) + 2 = 0
2(х2 – 2х + 1) – 2 + 3(у2 + 4у + 4) – 12 + 2 = 0
2(х - 1)2 + 3(у + 2)2 = 12
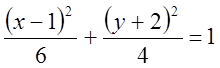 (1)
(1)
2. Перенесемо початок координат у точку О1(1, -2) і позначимо координати нової системи О1ХУ:
Х = х – 1, У = у – 2 (2)
3. Отримаємо канонічне рівняння кривої другого порядку, яка називається еліпсом.
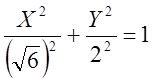 (3),
(3), ![]() в = 2.
в = 2.
4. ![]() ,
, ![]()
Таким чином, координати фокусів F1 і F2
еліпса запишемо у новій системі координат ![]() і
і
![]() .
.
5.
Ексцентриситет дорівнює
відношенню відстані між фокусами ![]() до довжини його
більшої осі
до довжини його
більшої осі ![]() .
.
Тобто 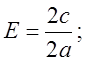
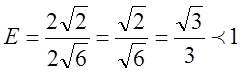 ,
, 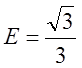
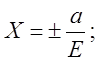 або
або 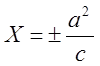 ,
,
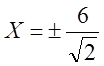 ,
, ![]() ,
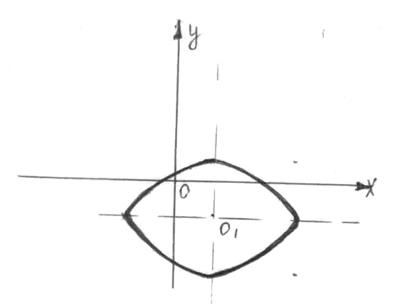
тобто дві прямі, перпендикулярні до більшої осі еліпса (див. рис. 20).
,
тобто дві прямі, перпендикулярні до більшої осі еліпса (див. рис. 20).
 |
Перевірка.
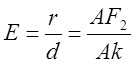 , де
, де
![]()
|
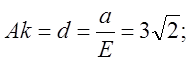
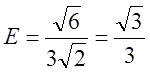 .
.
4.7Полярна система координат на площині
Положення точки на площині можна визначити іншим чином, взявши систему координат, відмінну від декартової системи ОХУ.
Розглянемо так звану полярну систему координат, яка складається з масштабної одиниці, з однієї осі, яка називається полярною віссю, та кута повороту цієї осі, який називається полярним кутом.
Полярна вісь – це промінь ОА, який виходить з полюса О і має додатній напрямок зліва направо.
Додатній поворот полярного кута j вважається в напрямі проти руху годинникової стрілки.
Координати довільної точки площини в такій системі
мають вигляд М(![]() ), тобто точка цілком
визначається двома координатами: відстанню
), тобто точка цілком
визначається двома координатами: відстанню ![]() точки
М від полюса О, або полярним радіусом, яку вважають першою
координатою, і полярним кутом j, який
вважають другою полярною координатою.
точки
М від полюса О, або полярним радіусом, яку вважають першою
координатою, і полярним кутом j, який
вважають другою полярною координатою.
Для того, щоб існувала взаємно однозначна
відповідність між множиною точок площини і множиною пар чисел (![]() ), треба розглядати лише так звані
головні значення полярних координат, тобто
), треба розглядати лише так звані
головні значення полярних координат, тобто ![]() ,
,
![]() .
.
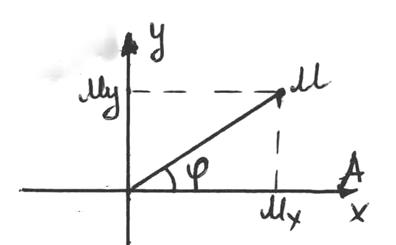
Запишемо формули перетворення, коли полюс полярної системи
суміщується з початком декартової системи координат, полярна вісь ОА – з
додатною піввіссю абсцис ОХ, а масштабна одиниця однакова в обох
системах, кут між полярною віссю і віссю ординат ОУ дорівнює ![]() (див. рис. 21).
(див. рис. 21).
![]() (1)
(1)
![]()
Формули (1) реалізують перехід від
полярних координат (![]() ) до декартових координат (х,
у).
) до декартових координат (х,
у).
|
![]() ,
, 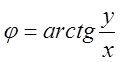 (2)
(2)
Для того, щоб знайти j в (2), треба врахувати збіг знаків х і ![]() , а також у і
, а також у і ![]() . Тоді матимемо перехід від (х, у)
до (
. Тоді матимемо перехід від (х, у)
до (![]() ).
).
Лінія в полярній системі координат задається рівнянням
![]() (3), яке зв’язує між собою
полярні координати точок, що належать цій лінії.
(3), яке зв’язує між собою
полярні координати точок, що належать цій лінії.
Лінію легше будувати в полярних координатах, якщо вона задається рівнянням у вигляді функції
![]() (4),
(4),
де аргументом є полярний кут, тобто друга полярна координата.
В цьому випадку лінію можна побудувати за допомогою точок,
надаючи аргументу ![]() значення через певний
проміжок, наприклад через
значення через певний
проміжок, наприклад через ![]() , чи
, чи ![]() , обчислюючи відповідні значення полярного
радіуса
, обчислюючи відповідні значення полярного
радіуса ![]() та використовуючи горизонтальну
таблицю:
та використовуючи горизонтальну
таблицю:
|
|
|
|
... |
|
|
|
|
... |
Розглянемо в полярних координатах рівняння деяких ліній.
Промінь. Якщо промінь виходить з полюса і утворює кут ![]() з полярною віссю, то його рівняння
з полярною віссю, то його рівняння ![]()
![]() .
.
Коло. Якщо центр кола радіуса R лежить у полюсі, то його рівняння ![]()
![]() .
.
Зауваження. Останні два рівняння описують координатну
сітку полярної системи (![]() ).
).
Приклад. Дано полярне рівняння лінії другого порядку у вигляді:
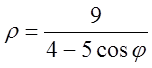 (
(![]() ).
).
1.
Побудувати лінію в
полярних координатах, надаючи аргументу j значення ![]() через проміжок
через проміжок ![]() та використовуючи горизонтальну таблицю.
та використовуючи горизонтальну таблицю.
|
і |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
5,62 |
2,25 |
1,41 |
1,1 |
1,0 |
1,1 |
1,41 |
2,25 |
5,62 |
- |
- |
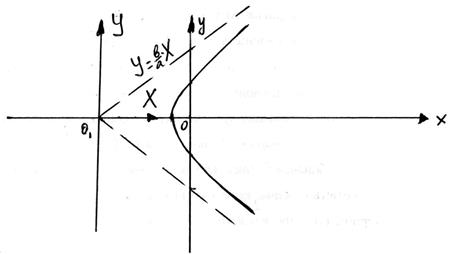 |
Рисунок 22
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.