Лабораторный практикум по курсу общей теплотехники, страница 65

,

получают формулы для расчёта скорости  w  и секундного расхода газа  m  при его докритических режимах течения:

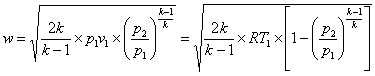                                   (10.9)

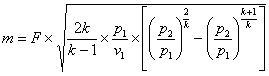                                      ;                      (10.10)

Здесь  k  –  показатель адиабаты  (для воздуха  k = 1,4);

           R  –  газовая постоянная  (для воздуха  R = 287 Дж/кг.град );

          T –  температура газа перед соплом,  К;

     p –  давление газа на входе в сопло,  Па;

          p –  давление газа на выходе из сопла,  Па.

          Как видно из приведённых формул, скорость истечения w и расход газа m  зависят от начальной температуры  T  и отношения давлений:

                                                               =                                               (10.11)

          Исследуя функцию  m = f()  на максимум путём дифференцирования зависимости  (10.10)  по параметру    и приравнивая первую производную нулю, можно получить выражение для определения критического значения величины  ,  при котором расход газа достигает своего максимума:

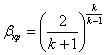                                                                                                (10.12)

          Таким образом,  критическое отношение давлений    зависит только от природы газа. Например, для воздуха, как для двухатомного газа ( k  = 1,4 ), величина   .

          Подставляя критическое отношение давлений    в формулу  (10.9), получают зависимость для расчёта максимальной скорости истечения из сопла

                                                    ,                                    (10.13)

которая соответствует местной скорости звука  a  в газе.

          Исследуя изменение расхода газа m (например, воздуха), определяемое формулой  (10.10),  при уменьшении    от 1 до 0  находим, что  m = 0  при =1 (т.е.  p= p)  и  при   = 0  (т.е.  p= 0).  В  промежутке  при  уменьшении величины   расход сначала возрастает, достигает максимума, а затем убывает  (линия AKB, рис. 10.1). Таким же образом от величины  зависит и изменение скорости газа.

             m     w                                                                     p