Линейно-аналоговые средства измерения с распределёнными параметрами
Исходной характеристикой динамических свойств устройств этой категории во временной области, как и в предыдущем случае, являются дифференциальные уравнения частных производных, например (15). Применение к уравнению метода функций Грина позволяет перейти от дифференциальных уравнений к интегральным уравнениям связи, подобно тому, как это делается для устройств с сосредоточенными параметрами. Ядра этих уравнений, то есть функции Грина для соответствующих задач, представляют собой импульсные характеристики линейных аналоговых устройств с распределёнными параметрами. Аналогично вводятся и переходные характеристики, передаточные функции, частные параметры. В отличие от СИТ с сосредоточенными параметрами, эти являются иррациональными функциями комплексной переменной В.
В качестве примера рассмотрим одномерное уравнение теплопроводности следующего вида:
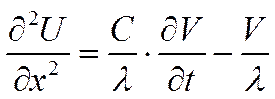 ,
(34)
,
(34)
где ![]() - удельная объёмная теплоёмкость.
- удельная объёмная теплоёмкость.
Подобным уравнением описываются разнообразные измерительные преобразователи, например построенные на цепочки схем или длинные линейные с распределённой ёмкостью или сопротивлением, или другие.
Моделями
таких устройств служат так называемые полуинерционные звенья. Их передаточными
функциями являются рациональные функции с переменной 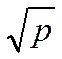 .
.
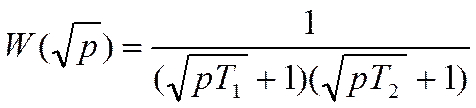 (35)
(35)
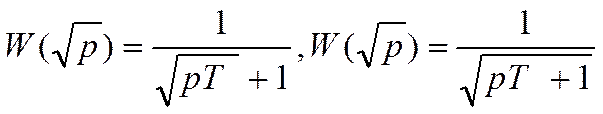
Переходные характеристики устройств с двумя последовательными передаточными функциями имеют следующий вид:
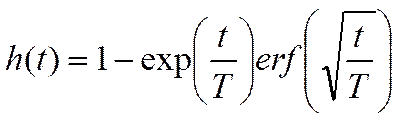 ,
(36)
,
(36)
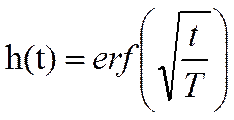 ,
,
где
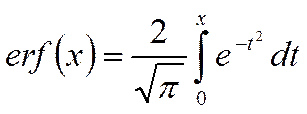 .
(37)
.
(37)
Линейные дискретные СИТ с распределёнными параметрами
Модели этого типа очень редки. Возможная область их применения – описание динамических свойств измерительных цепей, в которых используются первичные измерительные преобразователи с распределёнными параметрами, например, преобразователи неэлектрических сигналов в электрические. А обработка электрического сигнала предполагает его дискретизацию.
Нелинейные аналоговые СИТ с сосредоточенными параметрами
Нелинейные модели этих устройств разделяют на две группы:
§ слабо нелинейные,
§ существенно нелинейные.
Модели первой группы выражают остаточную нелинейность, то есть нелинейные эффекты, влияние которых конструктору этого устройства удалось снизить до уровня, позволяющего учесть их с помощью специальных погрешностей, таких как погрешность нелинейной градировочной характеристики или динамической характеристики.
Модели второй группы выражают принципиальную нелинейность, то есть эффекты, связанные с принципиальным преобразованием сигналов измерительных цепей. Зачастую эти нелинейности представляют собой цену, которую конструктор должен платить за достижение высоких метрологических характеристик СИТ: чувствительности, помехоустойчивости, широкого динамического диапазона.
Модели первой группы естественно строить на основе линеаризации, подразделяющейся на четыре вида:
Ø статическая,
Ø дифференциальная,
Ø гармоническая,
Ø случайная.
При линеаризации безинерционных нелинейных элементов с характеристикой, описываются с помощью уравнения (38):
![]() (38)
(38)
 ,
(39)
,
(39)
где ![]() - коэффициент линеаризации,
определяемый видом характеристики
- коэффициент линеаризации,
определяемый видом характеристики ![]() .
.
Модели второй группы основаны на использовании нелинейных операторов, чаще всего оператора Вольтерра, определяемого:
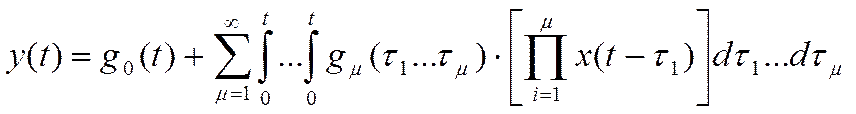 (14)
(14)
Эти
характеристики также могут быть названы импульсными. Также из уравнения (14)
следует, что модель с сосредоточенными параметрами может быть представлена в
виде соединения элементарных линейных звеньев повышенной размерности. Продолжая
аналогию, можно перейти к описанию устройств этой категории в комплексной и
частотной областях с помощью передаточных функций 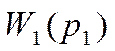 ,
,
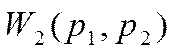 ,
, 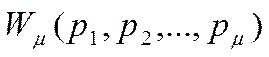 ,
каждая из которых определяет динамические свойства соответствующего
элементарного звена. Как и для линейных систем, путём замены переменной
,
каждая из которых определяет динамические свойства соответствующего
элементарного звена. Как и для линейных систем, путём замены переменной 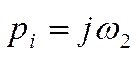 можно перейти к описанию свойств
нелинейных аналоговых устройств с сосредоточенными параметрами в частотной
области с помощью комплексных коэффициентов преобразования
можно перейти к описанию свойств
нелинейных аналоговых устройств с сосредоточенными параметрами в частотной
области с помощью комплексных коэффициентов преобразования 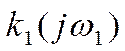 ,
, 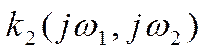 ,
,
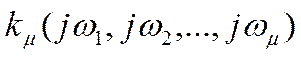 , АЧХ и ФЧХ.
, АЧХ и ФЧХ.
Нелинейные дискретные средства измерения с сосредоточенными параметрами
Динамика этой модели может описываться с помощью дискретного ряда Вольтерра:
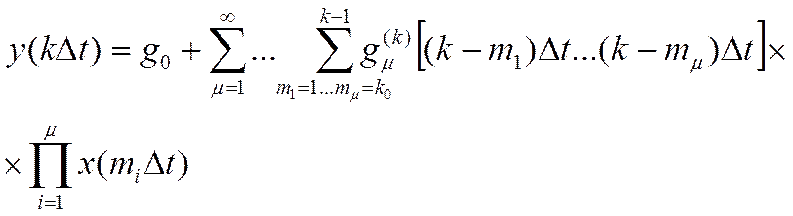 , (40)
, (40)
где ![]() - импульсная характеристика размера
- импульсная характеристика размера ![]() .
.
Применение к выражению (40) дискретного многомерного преобразования Лапласа позволяет ввести для этой модели передаточную функцию различной размерности.
Нелинейные средства измерения с распределёнными параметрами
Эти модели могут иметь различные формы, среди которых трудно выделить предпочтительные. Они характеризуются применительно к определённым типам СИТ.
Динамические характеристики и их классификация
Динамическим называют свойство СИТ, которое проявляется в том, что воздействие на них, то есть входной сигнал, в какой-либо момент времени обуславливает отклик этих средств в последующий момент времени.
Динамические свойства СИТ выражаются с помощью динамических характеристик. Динамическая характеристика – метрологическая характеристика устройства, отражающая связь информативного параметра переменного выходного сигнала с информативным или неинформативным параметром входного сигнала или влияющей величины.
Динамические характеристики разделяются по отношению к тем или иным параметрам входного сигнала на основные и дополнительные, по принципу полноты на полные и частные.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.