Сложнее обстоит дело с устройствами, непригодными для использования в статическом режиме (устройства с закрытым входом). Они могут иметь статическую составляющую погрешности (установка нулевого уровня, статическая погрешность выходного регистрирующего прибора). Однако нормированные условия применения, определяющие понятие основной погрешности, должны в этом случае относиться к динамическому режиму устройства. Например, нормированный динамический режим преобразователя переменного давления может быть мгновенным синусоидальным преобразователем давления на задней части. Коэффициент преобразования преобразователя – аналого-статический коэффициент преобразования погрешности измерения.
Математическое описание динамических режимов СИТ
В соответствии с определением динамического режима СИТ, не содержащего в себе других устройств, этот режим характеризуется изменением во времени выходного сигнала. Входной сигнал данного СИТ также является переменным. Математическое описание динамического режима должно позволить выразить связь входного и выходного сигналов, совпадающих в определённый момент времени. Связь может быть выражена в виде операторного уравнения:
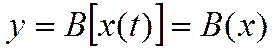 ,
(10)
,
(10)
где ![]() - оператор, отражающий характер
отклика устройства на входной сигнал. Область определения и область значений
его зависят как от свойств сигнала
- оператор, отражающий характер
отклика устройства на входной сигнал. Область определения и область значений
его зависят как от свойств сигнала ![]() , так и от самого
средства измерения.
, так и от самого
средства измерения.
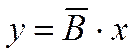
Если устройство может описываться линейной аналитической моделью с постоянными параметрами, то используются следующие формы данного уравнения:
1) операторное уравнение Вольтерра:
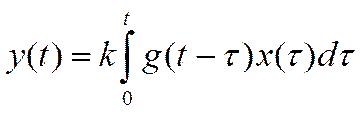 (11)
(11)
2) дифференциальное уравнение:
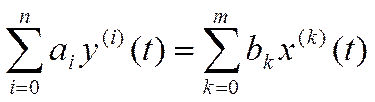 (12)
(12)
Нелинейные аналитические формы для СИТ весьма разнообразны. Важнейшие из них:
1) интегральное уравнение Хаммерштейна:
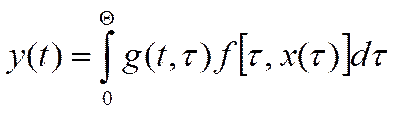 (13)
(13)
2) интегральное уравнение, определяющее оператор Вольтерра:
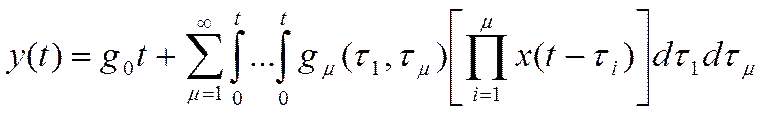 (14)
(14)
Динамический режим для аналоговых средств измерения описывается с помощью краевой системы – совокупности дифференциальных уравнений с частными условиями производной и краевых условий. Устанавливается связь между входным воздействием и переменным составляющей, которая характеризуется поведением объекта во времени и пространстве. Предполагается наличие связи перемены состояния. Эти дифференциальные уравнения чаще всего представляют канонические уравнения математической физики. Например, уравнение динамики теплоприёмника получается из анализа теплопроводности и в общем случае имеет вид:
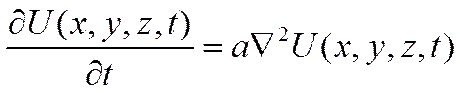 (15)
(15)
при краевых условиях:
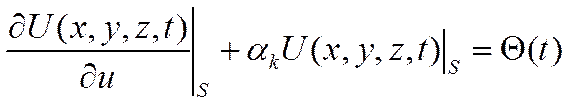 , (16)
, (16)
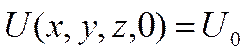 ,
,
где ![]() - коэффициенты теплопроводности и
температуропроводности материала термоприёмника;
- коэффициенты теплопроводности и
температуропроводности материала термоприёмника; ![]() -
коэффициент конвективного теплообмена между термоприёмником и средой;
-
коэффициент конвективного теплообмена между термоприёмником и средой; ![]() - температурные точки
термопроводности с координатами
- температурные точки
термопроводности с координатами ![]() в момент времени
в момент времени ![]() ;
; ![]() -
измеряемая температура;
-
измеряемая температура; ![]()
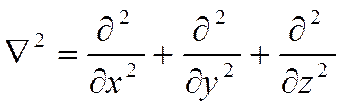 ;
; 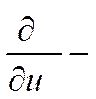 производная
по нормали к поверхности термометрического тела.
производная
по нормали к поверхности термометрического тела.
Обычно эти уравнения термоприёмников получают рассматриваемую задачу о распределении тепла для таких тел, как неограниченная пластина, цилиндр, стержень, шар. Показания термоприёмников соответствуют их объёмным температурам. В качестве выходной величины в стержневых термометрах используется температура начала стержня.
Основой описания динамического режима дискретных СИТ служит разностное уравнение, представляющее собой аналоговое дифференциальное уравнение для устройства непрерывного действия:
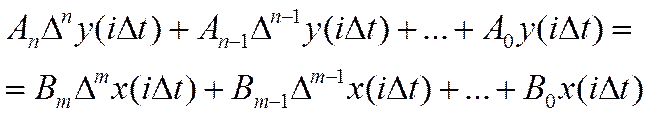 (17)
(17)
Введём оператор смещения:
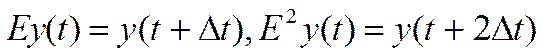
Тогда уравнение (17) можно записать так:
![]()
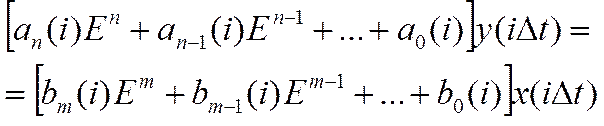 (18)
(18)
Для устройств с постоянным
параметром коэффициенты 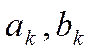 не зависят от
не зависят от ![]() .
.
Уравнение (18) можно
рассматривать как рекуррентное соотношение, с помощью которого при задании
значений 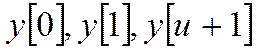 находят последовательно смещённые
значения
находят последовательно смещённые
значения ![]() .
.
Основным инструментом
анализа уравнений (17) и (18) служит Z-преобразование. Его применение к обеим частям выражения (18) при
постоянных частях коэффициентов 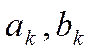 и при нулевых
начальных условиях даёт уравнение:
и при нулевых
начальных условиях даёт уравнение:
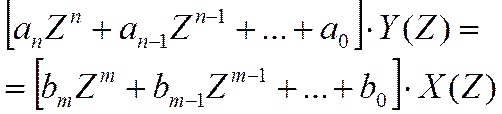 , (19)
, (19)
где ![]() - входное отображение входного и
выходного сигналов соответственно.
- входное отображение входного и
выходного сигналов соответственно.
Спектр дискретного сигнала, например АЦП, выражается формулой:
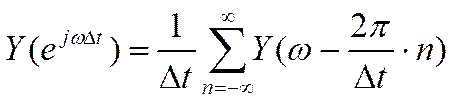 (20)
(20)
При условии соблюдения условия теоремы Котельникова (см. 21) этот сигнал может быть восстановлен без искажений.
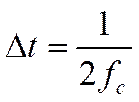 ,
(21)
,
(21)
где ![]() - верхняя граница частоты спектра
непрерывности выходного сигнала.
- верхняя граница частоты спектра
непрерывности выходного сигнала.
Аналогово-дискретные устройства можно рассматривать как аналоговые при соблюдении некоторых условий. С другой стороны, при использовании аналоговых устройств, измерительная информация в конечном итоге представляется в цифровой форме. Единое описание динамических свойств аналоговых и дискретных СИТ особенно важно при совместном использовании систем с выходом на ЭВМ.
Динамические свойства средств измерения
Модели средств динамических измерений и их характеристики.
Общие модели средств измерения разделяются по следующим признакам:
1) справедливости или несправедливости для них принципа суперпозиции сигналов,
2) существенности или несущественности имеющих место в них волновых эффектов,
3) непрерывности или дискретности входного и выходного сигналов.
По первому признаку модели бывают:
· линейные,
· нелинейные.
По второму признаку:
Ø с распределёнными параметрами
Ø с сосредоточенными параметрами
По третьему признаку модели подразделяют на:
§ аналоговые,
§ дискретные.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.