Динамические измерения. Проблемы динамических измерений. Входные сигналы и измеряемые величины. Погрешности динамических измерений, страница 15

Для оценивания шестого слагаемого необходимо учесть погрешности способов вычислений и используемых средств вычислительной техники. К этим погрешностям относятся погрешности интерполяции и экстраполяции, погрешности приближения интегрирования, погрешности округления, обусловленные разрядностью ЭВМ и т.д. При оценивании этой составляющей вместо В_Д и Х_Д в случае необходимости  должны быть использованы В_Н и Х_Н. Как видно, оценивание рассмотренных составляющих суммарной погрешности специально для конкретной измерительной задачи, поскольку исходные данные обусловлены этой задачей. Исключением является третья составляющая, вызванная отличием оператора В_ДТ, характеризующего динамические свойства СИ данного типа, от требуемого оператора В_Н. При оценивании этой составляющей основная сложность состоит в определении аргумента функционала Ф_Н. равного , или в общем случае

Рассмотрим оценивание этого аргумента. Операторы В_Н и В_ДТ выражают в совокупности статические и динамические свойства СИ. В практике эти свойства нормируют, контролируют и определяют раздельно, поэтому в выражениях для погрешности измерений выделяют статический коэффициент преобразования К(х), в общем случае зависящий от уровня входного сигнала (но не от его временных характеристик), и оператор  выражающий динамические свойства СИ, в общем случае нелинейный. Операторы К и удается выделить в следующих положениях:

1 элементы устройства, реализующие эти операторы структурно разделены. В этом случае, если операторы применяются в порядке К, В т.о.

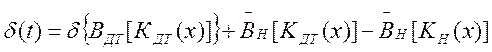                                              (6)

Где                                                            (7)

Если порядок применения операторов обратный то

                                                   (8)

Где                                                                           (9)

2. Статический коэффициент преобразования СИ не зависит от входного сигнала, а преобразование линейно. Этим условиям отвечают свойства большинства устройств, которые в своей области применения могут рассматриваться как линейная система. Погрешность измерений, приведенная ко входу:

                                                                          (10)

4.  Требуемое преобразование входного сигнала является тождественным

Это наиболее распространенный случай применения СИ в динамическом режиме, включающий в себя измерительные преобразования и регистрацию переменного сигнала. В этом случае приведенная к входу устройства погрешность измерений:

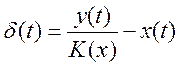                                                                                           (11)

Это выражение может служить для оценивания как общей погрешности измерений с регистрацией, так и погрешности регистрации в зависимости от того, учтена или нет в сигнале в сигнале y(t) погрешность отсчета. То же самое справедливо относительно измерительного преобразования, если в измерительной цепи за преобразователем следует отсчетное устройство или показывающий прибор.

Методы оценки погрешностей измерения инвариантны к физической природе величин y(t) и x(t). Нужно лишь учитывать, что если y(t) и x(t) выражают различные физические величины, то коэффициент К_Н будет размерным благодаря чему размерности обеих частей (6) совпадают с размером у, а (10) и (11) с размером х.

Динамические погрешности измерения постоянных величин.

Динамическую погрешность при измерении постоянной величины можно рассматривать как дополнительную в зависимости от измерительной задачи:

1.  Измерение постоянной величины с экстраполяцией к установившемуся значению.

Это случай измерений, включающий в себя следующие операции:

1)  подача на вход средства измерения постоянно изменяющуюся величину.

2)  регистрацию выходного сигнала в течении известного интервала времени

3)  расчет по значениям зарегистрированных сигналов и известным динамическим свойствам СИ измеряемой величины.

Такой способ измерения принимается в случае, когда ограничены или время измерения или допускаемый уровень входного и выходного сигнала. Примером может служить измерение высокой температуры среды с помощью термопары с относительно низкой температурой разрушения. Термопара погружается в среду на такое короткое время, которое позволяет избегнуть ее разрушения, но остается недостаточным для установления сигнала – выходного сигнала СИ, имеющий передаточную функцию вида:

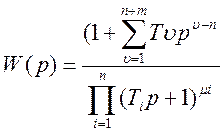
имеет следующий вид: ,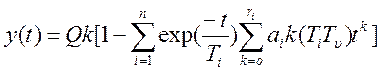

где k- статический коэффициент преобразования, r_i=, - известные дробно-рациональные выражения относительного коэффициента передаточной функции.

Оценка измеряемой величины находиться по среднему значению сигнала в момент времени t=t₀ на основании номинальной переходной характеристики:

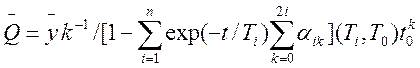                                                        (12)

Относительная погрешность оценки равна:

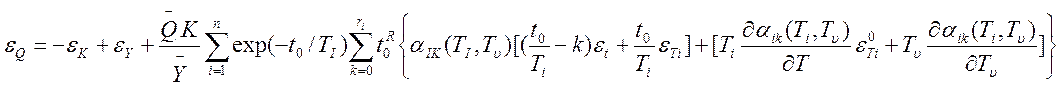(13)

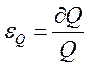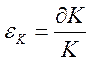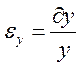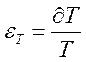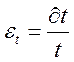, , , ,   погрешность фиксации или изменения времени

 - допустимое отклонение коэффициентов Т_i и T от номинальных или погрешность их определения.

-  допускаемое отклонение коэффициента К от номинального или абсолютная погрешность (статическая погрешность средства измерения)

 - погрешность отсчитывания

2.  Измерение постоянного параметра переменной величины.

В этой задаче предполагают, что преобразование разделено на преобразование переменного сигнала в переменный и переменного в постоянный. Это соответствует условию когда переменная величина  вначале регистрируется, а затем результаты регистрации обрабатываются с целью получения искомого параметра, а также, когда измерение проводиться с помощью комплекса СИ, для каждого из которых нормированы динамические свойства.

Обозначим С – результирующий оператор преобразования переменных сигналов  в СИ (при измерении с экстраполяцией это оператор регистрации,  а через  - функционал определяющий преобразование результирующего переменного сигнала в постоянный (при измерении с экстраполяцией – этот функционал является алгоритмом обработки). Функционал  в общем случае может быть отличным от Ф, и отличие  от Ф является одним из источников погрешности. Для линейного функционала Ф можем получить, преобразовав величины 2-го порядка