Динамические измерения. Проблемы динамических измерений. Входные сигналы и измеряемые величины. Погрешности динамических измерений, страница 2

1.  Определение последовательности значений величин, изменяемых во времени

2.  Измерение параметров однократно реализованных величин (например, амплитуда одиночных импульсов), преобразование и регистрация выходного сигнала

3.  Динамические измерения постоянной величины (например, измерение постоянной температуры) с экстраполяцией

Измерения		Статические		Динамические
		1	2	1	2
Измеряемая величина		==	==	==	~
Сигнал	Входной	==	~	~	~
	Выходной	==	==	~	~

 В методологическом аспекте динамические измерения означают переход от измерения скалярных величин к измерению векторных величин, в общем случае бесконечно верных, переход от измерений с числовым результатом к измерениям с результатом в виде функции. Переход от измерений с целью определения постоянной величины к измерениям с целью определения зависимости одной величины от другой (времени).

Таким образом, по узаконенной классификации измерений динамические измерения могут быть отнесены к совместным измерениям интересующих величин и времени. Поскольку они представляют собой процессы, проходящие во времени, необходимо определить их характеристики. Начало измерения – момент времени, в который СИТ приводится во взаимодействие с объектом исследования. Измерение заканчивается получением оценок измеряемой величины и погрешности. Измерения включают два этапа:

1)  наблюдение

2)  обработка экспериментальных данных

Наблюдение начинается с начала измерения и заканчивается регистрацией показаний. Следует иметь в виду, что измерения представляют этап подготовки, содержание которого является формулировкой задачи, выбор или конструирование СИТ.

Входные сигналы и измеряемые величины

Взаимодействие объекта исследования и средства измерения вызывает появление сигнала, пропорционального измеряемой величине. Они не совпадают. Различие в том, что одной и той же физической величине, создающей входной сигнал, может соответствовать ряд измеряемых величин. Эти величины (параметры процессов) на модели исследуемого объекта соответствуют функциональным. Справедливы следующие постулаты:

1.  В рамках принятой модели объекта исследования существует измеряемая величина и её истинное значение. Следствие – для данной конкретной физической величины существует множество значений

2.  Измеряемая величина постоянна. Следствие – для измерений при переменной конкретной физической величине необходимо определить постоянство её параметров, то есть измеряемую величину

На основании постулатов и их следствий рассмотрим содержание задач, решаемых с помощью динамических измерений.

Определение величины, изменяющейся во времени, производится в конечном итоге для временной зависимости величины. Поскольку требуется определить……...

то можно говорить не об одном, а о многих измерениях. В каждом должна быть мгновенная величина (соответствующая определённому моменту времени). На заданном интервале времени наблюдается непрерывная величина. Число этих моментов времени, соответствующее числу измерений мгновенной величины, может быть или конечным (дискретные динамические измерения), или бесконечным (аналоговые). В конечной разрешающей способности средств измерения, они производят усреднение входного сигнала. Интервал усреднения при дискретных измерениях фиксировано-связан, а при аналоговых – является скользящим. Изменение аналоговой величины является постоянным, то есть фиксированным, и вводится с помощью функционалов.

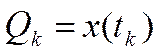,(1)

где  - заданный момент времени.

Функционалом называют соотношение, которое заданной функции ставит в соответствие число, то есть отображает определённое число функций на числовую ось или на участок.

При измерении преобразований переменного сигнала и регистрации изменяющейся величины измеряемые величины определяют аналогичным образом, но нужно иметь в виду, что измерение преобразований и регистрация – незавершённые измерения.

При измерении параметров однократной реальной величины определяют измеряемую величину, то есть параметр вводится с помощью функционала. Например, пиковое значение импульса определяется функционалом.

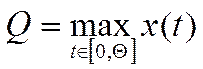                                               ,                                                     (2)

где Θ – длительность импульса.

При динамических измерениях постоянных величин она определяется как в обычном статическом режиме, то есть на статической модели. Сигнал на входе средства измерения изменяется во времени, причём характер изменения может быть различным. Явление, происходящее в СИТ, и его отклик тесно связаны со свойствами этого сигнала.

Для анализа сигналы разделяют на детерминированные и случайные. Реальные сигналы – сочетание тех и других. В большинстве конкретных ситуаций обоснованно может быть принята первая или вторая модель.

Детерминированные сигналы могут быть непрерывными во времени или посланы дискретными сигналами, то есть импульсами. Те и другие могут быть периодическими или непериодическими. Из всех возможных непрерывных периодических сигналов наибольший интерес представляют две разновидности:

·  финитные – отличные от нуля лишь на конечном интервале времени,

·  с ненулевым установившимся значением.

Реальные дискретные сигналы имеют вид импульсов, как правило, периодических, с определённым параметром (пиковое значение, длительность). Их модели определяются тем, какого рода изменения информации в них заключены. В одном случае каждый импульс содержит всю информацию о свойствах исследуемого объекта в момент появления импульса, а повторный импульс позволяет судить о постоянстве свойств. Кроме того, она создаёт избыточность, которая облегчает обработку сигнала и повышает достоверность результата. В этом случае временные характеристики импульсов и измерительного устройства, на которое они воздействуют, соизмеримы и каждый импульс должен рассматриваться как аналоговый сигнал и для его описания используются формулы (1) и (2). В другом случае изменённая информация содержится во всей совокупности импульсов, которая, таким образом, представляет собой единый кодированный сигнал. Тогда каждый отдельный импульс несёт весьма малую часть общей информации, и эта часть заключена в значении какого-либо параметра в зависимости от способа кодирования.