Характеристический сигнал представляет собой математические абстракции, то есть ряд идеализированных реальных сигналов, поэтому их используют при анализе методов, и определение характеристик СИТ требует определения погрешности, обусловленной этой идеализацией. Характеристические сигналы можно рассматривать как предельные для семейств реальных сигналов при высоких или низких некоторых характеристических параметрах, например, единичная ступень может быть представлена как предел для сигнала с монотонным нарастанием к единичному установившемуся значению при стремлении к нулю длительности фронта нарастания, то есть:
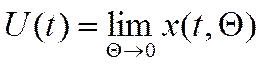 ,
,
где
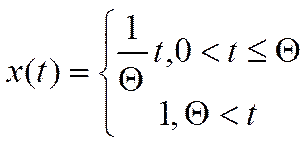 (4)
(4)
Введём значение прямоугольного импульса:
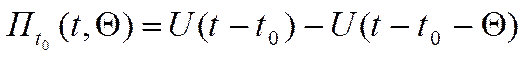 (5)
(5)
Тогда дельта-импульс можно описать с помощью следующего соотношения:
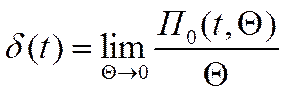 (6)
(6)
То есть дельта-импульс – предел для прямоугольного импульса с уменьшенной длительностью и растущим максимальным значением.
Гармонический сигнал может рассматриваться как предел для узкополосного сигнала при сужении полосы частот. Другие типовые испытательные сигналы чаще всего конструируются на основе этих характеристик и, соответственно можно выделить три группы сигналов:
1) ступенчатые с ненулевым установившимся значением,
2) финитные или импульсные, равные нулю вне определённого интервала времени,
3) периодические сигналы.
Среди ступенчатых и импульсных наиболее часто используются сигналы с монотонным нарастанием и с резонансным. Наиболее распространены среди ступенчатых сигналов сигналы с линейным нарастанием. Их распространение объясняется тем, что на практике закон нарастания сигнала зачастую неизвестен или требует для своего определения сложных методов. И поэтому линейно нарастающий сигнал служит первым приближением. Другой часто используемый сигнал – сигнал с экспоненциальным нарастанием.
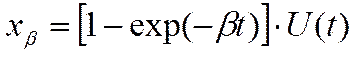
Распространение этого сигнала объясняется тем, что в основе принципа действия многих генераторов испытательных сигналов лежит процесс заряда и разряда, как, например, в электрических цепях, содержащих конденсаторы, катушки индуктивности и т. д.
Среди импульсных сигналов выделяют:
ü прямоугольный импульс,
ü треугольный импульс:
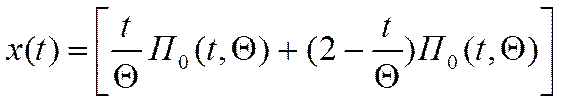 ,
,
ü синусоидальный импульс:
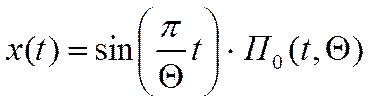 ,
,
Наиболее распространёнными периодическими сигналами являются последовательности прямоугольных и трапециидальных импульсов. В некоторых областях используются случайные испытательные сигналы. Например, турбулентные пульсации температуры при измерении параметров водных потоков. Эти сигналы предполагают стационарность и органичность. Таким образом, типовые испытательные сигналы имеют следующий вид:

С их помощью построены были сложные испытательные системы, например, прямоугольный импульс:
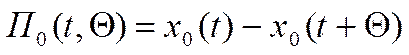 ,
,
системы с экспоненциальным нарастанием:
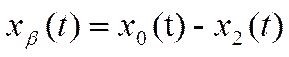 ,
,
синусоидальный импульс:
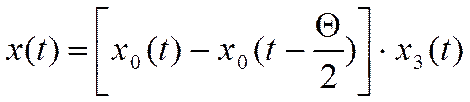 .
.
Реальные испытательные системы – источники этих моделей, а описание с их помощью лишь приближено.
Неточное описание обуславливает одну из составляющих, определяющих динамическую характеристику и при некоторых …………………………… прямых методов она может быть одной из существенных и даже определяющих динамических составляющих.
При реализации корреляционного метода определения динамической характеристики требуется случайный испытательный сигнал.
В метрологии, особенно в отрасли экспериментальных измерений, получили распространение псевдослучайные испытательные сигналы. Они представляют собой двоичные последовательности малой длины (М-последовательности) и имеют следующий вид:
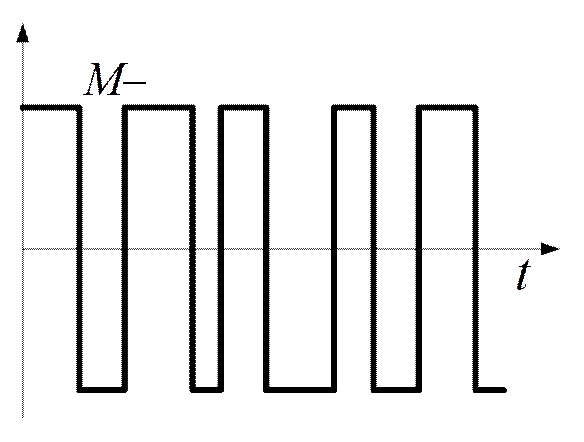
М-последовательности генерируются с помощью двоичных регистров сдвига и запускаются тактовыми импульсами. По своим спектральным характеристикам М-последовательность может быть приближена к белому шуму.
Псевдослучайные двоичные последовательные сигналы … длины обладают высокой воспроизводимостью цифровых сигналов. Эти сигналы обладают также широкой полосой частот, характерной для подобных сигналов, им присуща хорошая равномерность спектра. Кроме того, сигналы отличаются сравнительной простотой воспроизведения.
Качества испытательных сигналов определяются тем, насколько они отвечают необходимым требованиям к их временным и спектральным свойствам, точности воспроизведения или …………………
Общее соотношение во временной области, на основе которого могут быть установлены требования к точностным свойствам испытательных сигналов, имеет следующий вид:
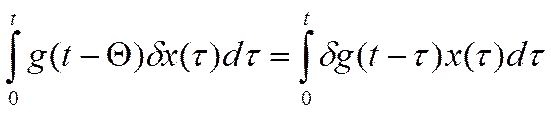 ,
(7)
,
(7)
где ![]() - параметры воспроизведения или
регистрации испытательных сигналов,
- параметры воспроизведения или
регистрации испытательных сигналов, ![]() - параметры
определения характеристики,
- параметры
определения характеристики, ![]() - реальный испытательный
сигнал.
- реальный испытательный
сигнал.
Исходя
из …………………………., модуль ![]() - допускаемая погрешность
импульсной характеристики, их выражения (7) получаем:
- допускаемая погрешность
импульсной характеристики, их выражения (7) получаем:
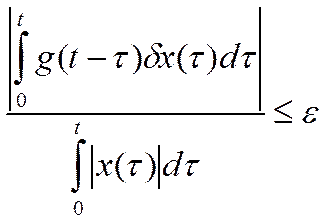 (8)
(8)
Это неравенство отображает необходимое условие, которому должен удовлетворять испытательный сигнал. Для его выполнения достаточно соблюдать следующее неравенство:
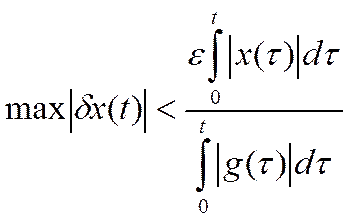 .
(9)
.
(9)
А в частотной области неравенству (8) соответствует соотношение:
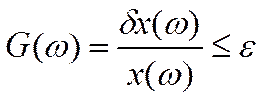 .
(10)
.
(10)
Неравенства (9) и (10) полезны при анализе сигналов в качестве испытательных, так как они позволяют однозначно решить вопрос о непригодности исследуемого сигнала. А достаточные условия пригодности сигналов могут быть установлены на основе исследования конкретных методов определения динамических характеристик.
Требования к спектральным свойствам испытательных сигналов определяются тем, что критерий качества сигналов, как испытательных, должен быть основан на достаточной ……………… данной установки исследуемым устройствам.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.