Динамические измерения. Проблемы динамических измерений. Входные сигналы и измеряемые величины. Погрешности динамических измерений, страница 14

Существенный вопрос о зависимости составляющих погрешности. Поскольку независимы причины, вызывающие взаимное отклонение операторов в выражении (5) то зависимость и независимость соответствующих составляющих обусловлена лишь характером сигнала. В том случае, когда х_Д – случайная функция составляющие  и  как случайные величины взаимно коррелированны. При детерминированном сигнале х_Д эти составляющие независимы.

Различным измерительным задачам отвечают частные случаи соотношения (5).

1)  Регистрация или масштабирование преобразования сигнала.

К ним относятся запись измеряемой величины во времени, цифровая регистрация, измерительное преобразование сигнала неэлектрической величины в электрический сигнал, измерительное усиление и т.д. В этом случае функционал Ф_Н не задан, а оператор В_Н представляет собой масштабный коэффициент (номинальный коэффициент преобразования) К_Н. Т.о. измеряемая величина

                                                                                                 (2а)

Результат измерений

                                                                                                (3а)

погрешностей

                                         (5а)

Где  - тоже что и в (5) с учетом того, что В_Н=К_Н.

2)  Линейное функциональное преобразование сигнала.

К нему относятся интегрирование, дифференцирование сигнала и т.д. В этом случае функционал не задан и измеряемая величина

                                                                                                     (2б)

Результирующий

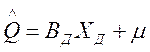                                                                                               (3б)

Погрешность:                     (5б)

3)  Измерения параметра переменного сигнала (линейного функционала). К нему относятся нахождение интегрального значения сигнала на заданном интервале времени, среднее значение, значения в фиксированный момент времени и т.п. В этом случае оператор В_Н является тождественным () и измеряемая величина , а результат измерения в общем случае определяется вычислением (3)

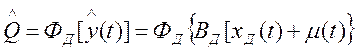
Если динамические свойства СИ можно не учитывать, то

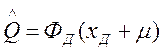                                                                                             (3в)

И погрешность

                           (5в)

Для оценивания первого слагаемого в (5) необходимо установить зависимость оператора В_Н от влияющего сигнала или от каждой из влияющих величин Поскольку при оценивании погрешностей не требуется высокой точности, то можно воспользоваться зависимостями от  не индивидуального (В_ДЭ), а типового оператора СИ. Указанные зависимости устанавливаются с помощью функций влияния. При нормированных (известных) функциях влияния должно быть определено совокупное изменение В_ДТ под воздействии  с учетом взаимозависимости влияний отдельных влияющих величин. Далее следует рассчитать уменьшение функционала Ф_Н от отклика типового устройства. При расчете вместо неизвестного сигнала х_Д может быть использован подходящий сигнал х_Р из совокупности возможных (рабочих) входных сигналов СИ.

Ак правило, влияющие величины заданы пределами допускаемых отклонений от указанных значений. При параметрическом задании оператора В_ДТ =  В_ДТ() и представлении функции влияния в форме зависимостей параметров () задача формулируется как нахождение экстремума функции многих переменных. В частности линейных функций влияния

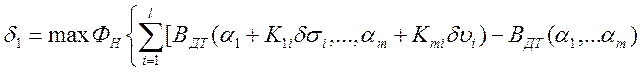
Для оценивания второго слагаемого в (5) ьребуется знать отклонение индивидуального оператора В_ДЭ от типового В_ДТ. Эти сведения в обобщенном (по совокупности устройств данного типа) виде представляются в результате нормирования полных характеристик. Как и выше, задача сводиться к нахождению экстремума функции многих переменных:

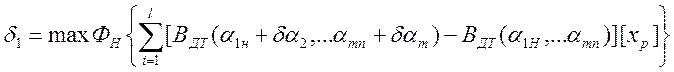
Третьи слагаемые оценим позже и перейдем к следующим.

Оценивание четвертого слагаемого предполагает знание функциональной зависимости погрешности отсчитывания от времени (от моментов дискретизации выходного сигнала устройства). На практике такая зависимость, как правило, неизвестна. Поэтому целесообразно представить  как случайную функцию времени с известным распределением вероятностей, например, равномерным или усеченно нормальным в заданных границах, которые в общем случае могут зависеть от времени. При этом оценка составляющей может быть рассчитана с использованием функционала Ф_Н вместо Ф_Д, который чаще всего остается неизвестным.

Для оценивания пятого слагаемого прежде всего изучить обратные влияния СИ на объект исследований, который позволит оценить отличие номинального входного сигнала х_н от истинного х_и, присущего невозмущенному объекту. Кроме того, необходимо получить сведения о помехе. Влияние СИ на объект обуславливает систематическую погрешность, случайный разброс которой по множеству устройств данного типа обычно невелик, в целом эта погрешность должна оцениваться пределами допускаемых значений. Помеха в общем случае содержит детерминированную и случайную часть. Для определения характеристик случайной части рассматриваемой составляющей необходимы подробные сведенья о вероятных свойствах помехи. На практике эти сведения, как правило, отсутствуют. Поэтому обычно ограничиваются оцениванием эмпирических характеристик случайной части (дисперсии, СКО), для чего используют имеющиеся сведенья или обоснованные предположения о спектральных (корреляционных) свойствах помехи . Если СИ приводиться во взаимодействие с объектом спустя определенное время после подключения к источнику питания, достаточное для установления стационарного режима работы, то случайная часть оцениваемой составляющей будет представлять собой стационарную случайную функцию, дисперсия которой определяется спектральными свойствами и частотной характеристикой средства.