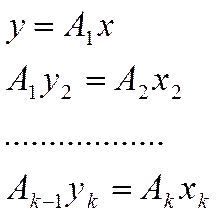 (6)
(6)
Введём
обозначения: 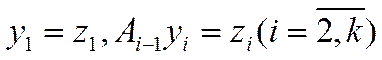 . Тогда выражение (6) можно
переписать следующим образом:
. Тогда выражение (6) можно
переписать следующим образом:
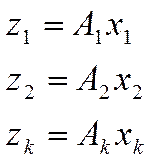
Где ![]() входит в экспериментальный сигнал, а
входит в экспериментальный сигнал, а
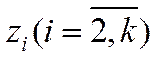 получаем из экспериментальных данных
путём решения прямой задачи динамики.
получаем из экспериментальных данных
путём решения прямой задачи динамики. 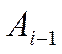 ,
необходимое для вычисления
,
необходимое для вычисления ![]() , находим из
предыдущего уравнения.
, находим из
предыдущего уравнения.
Таким
образом, для реализации этой схемы требуются определять полные динамические
характеристики системы и решать их на основании прямой задачи динамики. Из
этого анализа следует, что реализация схемы при рассмотренных выше условиях не
требует точного знания сигналов 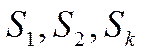 . Нужны лишь сведения
о том, что эти сигналы являются достаточно широкополосными, чтобы полностью
выявить свойства исследуемого измерительного преобразователя. Рассмотрим также
вопрос о нарастании погрешности определения характеристик в этой системе.
. Нужны лишь сведения
о том, что эти сигналы являются достаточно широкополосными, чтобы полностью
выявить свойства исследуемого измерительного преобразователя. Рассмотрим также
вопрос о нарастании погрешности определения характеристик в этой системе.
Пусть ![]() - разрешающая способность алгоритма
определения характеристики для
- разрешающая способность алгоритма
определения характеристики для ![]() уровня схемы.
Тогда погрешность
уровня схемы.
Тогда погрешность 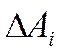 определения оператора
определения оператора ![]() равна:
равна:
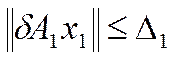 .
.
Записываем поочерёдно выражение (6):
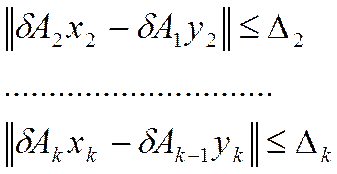 (7)
(7)
Следовательно, из этих соотношений могут быть получены лишь оценки операторов снизу. Поэтому выражение (7) можно рассматривать как общую схему нарастания погрешности в иерархической схеме определения динамической погрешности. Для конкретных методов определения характеристик, включающих конкретные испытательные сигналы и способы обработки экспериментальных данных, могут быть разработаны алгоритмы оценки погрешности при передаче динамических свойств. Разработка этих алгоритмов базируется на результатах, которые получены при разработке их свойств и описывают и методы динамических характеристик.
Требования к характеристикам средств контроля динамических характеристик СИТ
При установлении этих требований исходят из требований точности определения динамических характеристик. Под требованиями к средствам аттестации контроля понимают требования к их динамическим свойствам. Рассмотрим обобщённую структурную схему устройства для определения и контроля СИТ. Она содержит кроме исследуемого СИТ ГИС – генератор испытательных сигналов, регистрирующий прибор РП, измерительный преобразователь ИП, например, измерительный усилитель.

Рассмотрим
случай, когда можно раздельно устанавливать требования к спектральным и
точностным характеристикам сигнала ![]() . При этом
требования к спектру его могут устанавливаться независимо от методов и средств
измерения и сигнала
. При этом
требования к спектру его могут устанавливаться независимо от методов и средств
измерения и сигнала ![]() . Эти требования –
требования к частотным характеристикам ГИС, которые можно выразить как
требования к частотным свойствам преобразователя П, характеристического сигнала
…………… в реальных сигналах
. Эти требования –
требования к частотным характеристикам ГИС, которые можно выразить как
требования к частотным свойствам преобразователя П, характеристического сигнала
…………… в реальных сигналах ![]() . Если
. Если ![]() - передаточная функция
преобразователя П, то
- передаточная функция
преобразователя П, то ![]() может быть представлена
как:
может быть представлена
как:
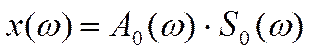 ,
(8)
,
(8)
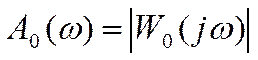 .
.
В
зависимости от формы испытательного сигнала, которая легче всего
воспроизводится в данной области измерения, устанавливается сигнал ![]() . Для сигналов с ненулевым
установившимся значением, для импульсных и периодических сигналов из выражения
(8) получаем:
. Для сигналов с ненулевым
установившимся значением, для импульсных и периодических сигналов из выражения
(8) получаем:
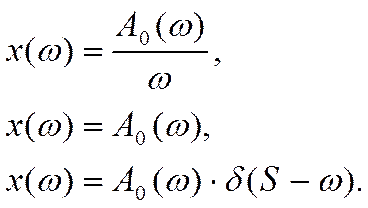 (9)
(9)
Таким
образом, требования к ![]() переносятся однозначно на
АЧХ
переносятся однозначно на
АЧХ 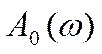 и, следовательно, в рассматриваемом
случае для решения задачи могут быть использованы методы, изложенные при
рассмотрении прямых методов нахождения динамических характеристик.
и, следовательно, в рассматриваемом
случае для решения задачи могут быть использованы методы, изложенные при
рассмотрении прямых методов нахождения динамических характеристик.
Если
же речь идёт об определении частотных характеристик в ограниченном диапазоне
частот, утверждение независимости требований сигналов ![]() и
и
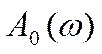 от методов и средств регистрации
сигнала
от методов и средств регистрации
сигнала ![]() строго справедливо. При определении
же совокупности АЧХ и ФЧХ как полной характеристики это утверждение уже не
является строгим, так как реальные испытательные сигналы не могут обеспечивать
определение частотных характеристик на всей полуоси от 0 до +∞. Происходит,
как правило, потеря информации о хвосте, то есть высокочастотной части средства
измерения. Эта потеря обусловлена конечной шириной спектра
строго справедливо. При определении
же совокупности АЧХ и ФЧХ как полной характеристики это утверждение уже не
является строгим, так как реальные испытательные сигналы не могут обеспечивать
определение частотных характеристик на всей полуоси от 0 до +∞. Происходит,
как правило, потеря информации о хвосте, то есть высокочастотной части средства
измерения. Эта потеря обусловлена конечной шириной спектра ![]() и
и 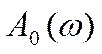 на
уровне погрешностей. Аналогичная потеря информации происходит в силу того, что
спектр выходного сигнала
на
уровне погрешностей. Аналогичная потеря информации происходит в силу того, что
спектр выходного сигнала ![]() не может быть
зарегистрирован на всей полосе от 0 до +∞ вследствие ограниченной частотной
полосы пропускания СР. Следовательно, при установке требований к ГИС и СР
исходя из допускаемой среднеквадратичной погрешности определения характеристики
нужно учитывать суммарную энергию потерь:
не может быть
зарегистрирован на всей полосе от 0 до +∞ вследствие ограниченной частотной
полосы пропускания СР. Следовательно, при установке требований к ГИС и СР
исходя из допускаемой среднеквадратичной погрешности определения характеристики
нужно учитывать суммарную энергию потерь:
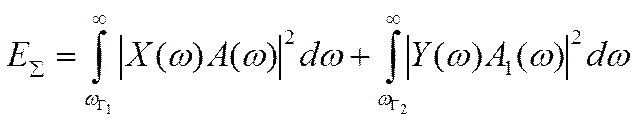 ,
(10)
,
(10)
где ![]() - АЧХ СИТ,
- АЧХ СИТ, 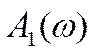 -
АЧХ средства измерения,
-
АЧХ средства измерения, 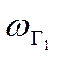 и
и 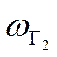 определяются из условия:
определяются из условия:
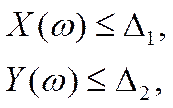
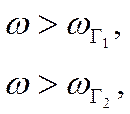
где ![]() и
и ![]() -
погрешности определения
-
погрешности определения ![]()
![]() и
и ![]() соответственно.
соответственно.
Если 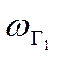 и
и 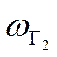 близки
друг к другу, то выражение (10) можно упростить:
близки
друг к другу, то выражение (10) можно упростить:
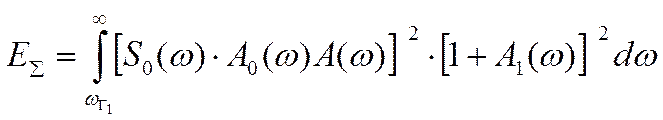 ,
(11)
,
(11)
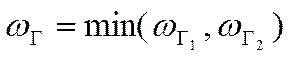 .
.
При
использовании гармонических сигналов подынтегральное выражение вместо
произведения 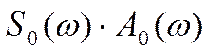 будет содержать:
будет содержать:
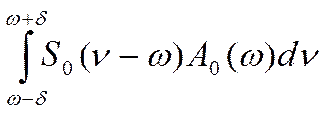
Для других характеристических сигналов из выражения (11) для сигналов с ненулевым установившимся значением получаем:
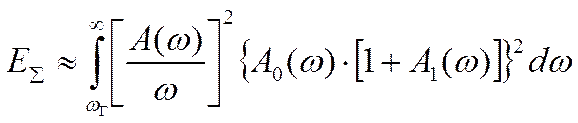 ,
,
для импульсных сигналов:
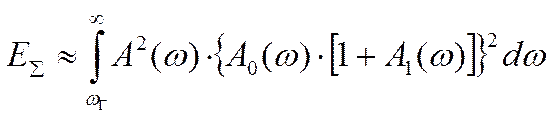 .
.
Этот же подход используется в тех случаях, когда нельзя разделить требования к спектральным и точностным характеристикам испытательных сигналов.
Рассмотрим структурную схему для прямого определения динамических характеристик.

В
реальном ГИС с помощью оператора ![]() преобразование
характеристического сигнала
преобразование
характеристического сигнала ![]() осуществляется с
погрешностью
осуществляется с
погрешностью ![]() . В результате испытательных данных
действительный оператор
. В результате испытательных данных
действительный оператор ![]() исследуемого СИТ
преобразует реальный испытательный сигнал
исследуемого СИТ
преобразует реальный испытательный сигнал ![]() в
выходной сигнал
в
выходной сигнал ![]() .
.
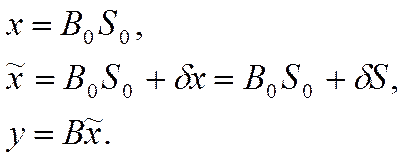
В
результате регистрации выходного сигнала ![]() с
помощью средства регистрации СР получается оценка
с
помощью средства регистрации СР получается оценка ![]() :
:
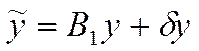 ,
,
где ![]() - номинальный оператор средства
регистрации,
- номинальный оператор средства
регистрации,
![]() - погрешность, учитывающая
отклонение реального оператора от
- погрешность, учитывающая
отклонение реального оператора от
номинального.
На
основании исходных данных ![]() и
и ![]() с помощью конкретного прямого метода
находится оценка
с помощью конкретного прямого метода
находится оценка ![]() оператора средства
измерения.
оператора средства
измерения.
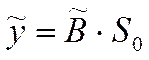 .
.
В операторной форме погрешность оценки будет равна:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.